二维非稳态导热微分方程_线性代数25——微分方程和exp(At)

微分方程指含有未知函数及其导数的关系式，解微分方程就是找出未知函数。未知函数是一元函数的，叫常微分方程；未知函数是多元函数的，叫做偏微分方程。常微分方程有时也简称方程。微分方程是一门复杂的学科，对于常微分方程来说，可以使用特征值和特征向量的知识求解。相关前置知识：

泰勒公式在0点展开的原因：多项式函数能够拟合非线性问题原理
　　　　求行列式：行列式和代数余子式
　　　　特征值和特征向量：特征值和特征向量
　　　 矩阵对角化：矩阵的对角化和方幂

常微分方程的一般解法

根据概念构造一个常微分方程：

　　目标是求得原函数u=u(t)的具体形式。通过积分求解：

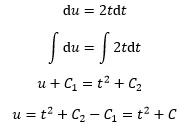
　　这就是最终答案的通解，C是任意常数。实际上这种解法就是利用了不定积分的知识：

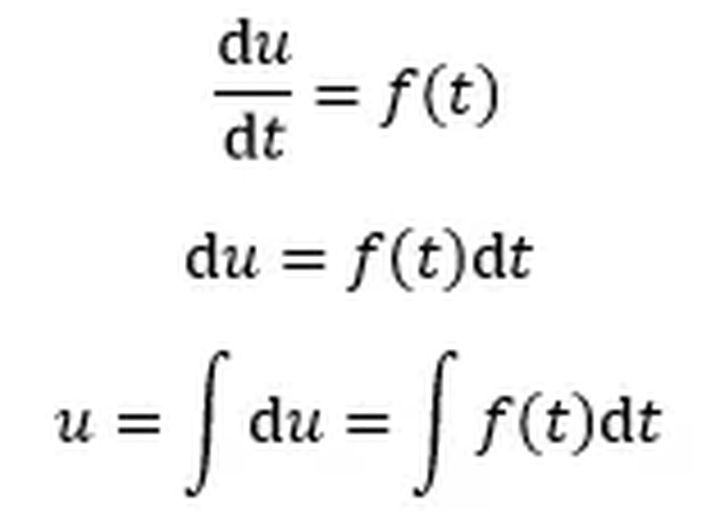
　　如果

，可以使用分离变量法的求解方式：

　　也就是说，当函数的导数是函数本身的时候，这个函数就是型如

的函数，由于

是任意常数，所以经常用C代替A，写成

的形式。

　　同理，对于

，微分方程的解是

。当t=0时：

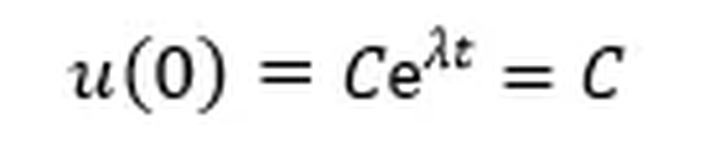
　　由于C是任意常数，因此可以取C=u(0)，得到

，这样做可以去掉常数C。在实际问题中，u可以表示关于时间t的函数，对于时间来说，通常可以把t=0看作初始条件。

常微分方程与矩阵

　现在将常微分方程扩展为常微分方程组，

，初始条件是t=0，初始值是

u(0)=(1,0)，求解微分方程：

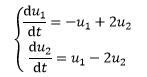
　　可以把微分方程组写成向量矩阵的形式：

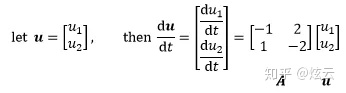
　　相当于将常微分方程中转换成了

的线性形式。

常微分方程的线性代数解法

对于

来说，

之间存在耦合（没有耦合就没必要写成方程组了&#x