高斯消元法c语言程序_【算法趣谈】高斯消元

    最近的数学课上，我们学习了高斯消元(Gauss elimination)，也就是解多元一次方程的一种通用解法。    在讲解计算机实现解多元一次方程前，我们先用人类的思维来解以下三元一次方程组：

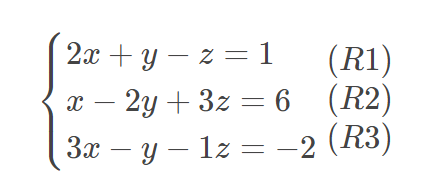
    如果要解出这个方程x、y、z未知数的值，我们需要通过消元的方法减少未知数，从而得到一个未知数的解，再将此未知数往原先的方程带，从而得到所有未知数的解。

对于这个三元一次方程组，我们可以把解未知数的步骤列出来：

    1、通过R1与R2的加减消元，将x消去，新的方程叫做R4，形式为:

                           ay+bz=k(a、b、k均为参数)

    2、通过R1与R3的加减消元，将x消去，新的方程叫做R5，形式为：

                           ay+bz=k(a、b、k均为参数)

    到此，原本的三元一次方程组就被化为了二元一次方程组。

    3、通过R4与R5的加减消元，将y消去，新的方程叫做R6，形式为：

                           az=b(z、b均为参数)

    到此，二元一次方程又被化简为了一元一次方程。

    4、求解z，再将z带入R4中，求解y。

    5、求解y，再带入R1中，求解x

    按照上面的步骤，我们就可以顺利地求出方程的三个未知数的解。

     但是，当方程的规模越来越庞大，或者方程的系数变得十分难算时，仅仅依靠双手，是完成不了计算的。这时，我们就需要借助计算机力量。

    可是计算机并不是像我们一样好说话，用中文说明一下就完了。要求计算机做事，就需要计算机能理解的东西。比如在C++语言中，计算机并不理解方程是什么东西，因此，我们需要将方程转化为它所理解的矩阵：

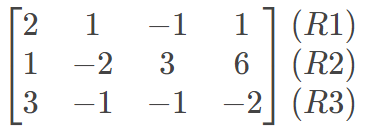
这是一个3*(3+1)的矩阵(3为方程组未知数数量)，其中的3行分别代表原方程组的三个方程，前3列每个数分别代表每个方程中x、y、z的系数，最后一列每个数分别代表所在行方程等号右边的常数。

而我们又需要把原来求解方程的步骤转化到矩阵上。

第一步，用R1和R2加减消元消去x。具体消去x的方式是，将R1除以R1中x的系数，这样让x的系数变为1。

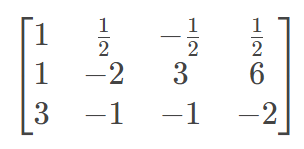
然后，我们让R2减去乘上R2的x的系数的R1(也就是R2-1*R1)，得出的结果替换原来R2的位置。

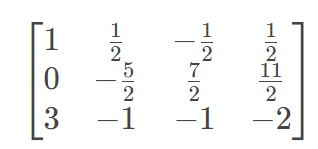
  第二步，我们用R1和R3进行加减消元，把x项消去。方法同第一步，让R3减去乘上R3的x的系数的R1(也就是R3-3*R1)，替换原来R3的位置。

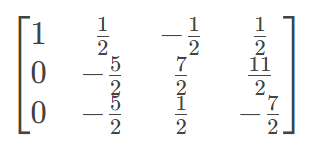
第三步，用R2和R3的加减消元把y消去，先把R2除以自己的y的系数。

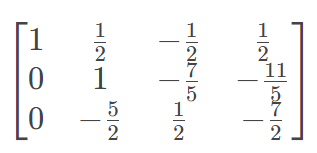
然后，让R3减去乘以R3的y的系数的R2(也就是R3-R2*(-5/2))

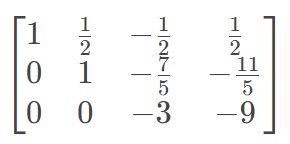
  第四步，很显然最后一个方程就是-3z=9, 能解出z等于3，于是把z=3带入上面的式子，得出y=2。最后，把z=3、y=2带入第一个式子，得出x=1。这样，我们就求出了方程的解是：

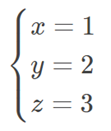
      到现在，有的同学会问，在解这个方程的过程中，很多步骤是很蠢的，比如加减消元R2和R3时，我们把R2先乘-2/5再除以-2/5。确实，这种步骤在人工解这道题时很多余。但是，既然是编程，我们需要找的是一种通用的解法，不是只针对于这个方程，而是全部的多元一次方程。比如说，如果另一个方程的x系数的最小公倍数很大，或者他们根本就是一些分数，我们平时用的寻找最小公倍数等简便的加减消元法就不起作用了，而这种通用解法却可以一直使用下去。

      回到正题，既然解决了这个方程，那么我们就可以扩展到解一个n元一次方程了。令一个n元一次方程的矩阵形式为：

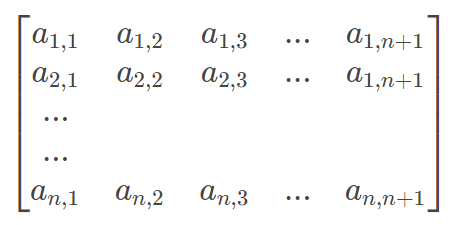
我们只需要按照刚才的步骤化简这个矩阵就ok了

第一步，让R1除以a(1,1)，然后从第二行到第n行，每一行式子都减去R1乘以这个式子的x的系数，也就是令Ri变成Ri-R1*a(i,1)。

第二步，让R2除以a(2,2)，然后从第三行到第n行，每个式子都减去R2乘以这个式子的y的系数，也就是令Ri变成Ri-R2*a(i,2)

第三步，就是处理R3，以此类推，一共进行n-1步，共消去n-1个未知数，剩下的是一个一元一次方程，能顺利求解。再将这个解依次带到前面的方程中，求出每个未知数的解。

那么，我们用c++来实现这个算法。

#include #include #include #include #include #define in(a) a=read()#define REP(i,k,n)  for(int i=k;i<=n;i++)#define INF 2147483646using namespace std;inline int read(){  int x=0,f=1;  char ch=getchar();  for(;!isdigit(ch);ch=getchar())    if(ch=='-')      f=-1;  for(;isdigit(ch);ch=getchar())    x=x*10+ch-'0';    return x*f;}double matrix[110][110];//这个数组是用来存储矩阵的double X[110];//这个数组是用来存储答案的int n; int main(){  in(n);  REP(i,1,n)    REP(j,1,n+1)        scanf("%lf",&matrix[i][j]);//读入这个矩阵  REP(i,1,n){    int target=i;    REP(j,i+1,n)      if(fabs(matrix[j][i])>fabs(matrix[target][i]))//把拥有当前消除未知数系数最高的式子移到上面(见附录)        target=j;    if(i!=target)         swap(matrix[i],matrix[target]);    double div=matrix[i][i];    REP(j,i,n+1)  matrix[i][j]/=div;//将当前行除以第一项，也就是Ri除以a(i,i)    REP(j,i+1,n){//消去下面所有行的当前未知数      double cof=matrix[j][i];//获得要被消行的未知数系数      REP(k,i,n+1)  matrix[j][k]=matrix[j][k]-matrix[i][k]*cof;// 让Rj-Ri*a(j,i)    }  }  X[n]=matrix[n][n+1];//最后一行的一元一次方程求解  for(int i=n-1;i>=1;i--){//把解逐步往上面的式子带     X[i]=matrix[i][n+1];     REP(j,i+1,n)  X[i]-=(X[j]*matrix[i][j]);  }  REP(i,1,n)  cout<" ";   return 0;}/*附录：关于为什么要把当前被消未知数最高系数的试题提到最上面，以用来消除其他式子的未知数。因为这样能减少误差。计算机是以浮点，也就是小数的形式存储数，那么数的除法难免会有误差。很明显，一个较小的数除以一个较大的数的误差会比较大的数除以较小的数小很多。所以我们用系数最高的未知数，来消去系数低的未知数*/

输入数据：

    ‍

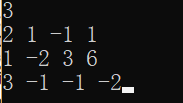
    输出数据： 

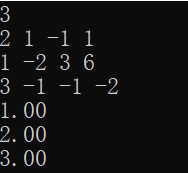
    程序成功地计算出了方程的解。只要改变n的值，此程序就能解n元一次方程。通过代码的循环层数，能看出此算法的时间复杂度是O(n³)。也就是程序在1s内可以解出1000元一次方程。

    以上就是高斯消元的全部内容了，大家学会以后可以写在电脑上，以后做数学作业时就可以秒出答案了。