动态赋值_动态的赵爽弦图【GeoGebra制作教程】

勾股定理：如果直角三角形的两条直角边长分别为a,b，斜边长为c，那么

。

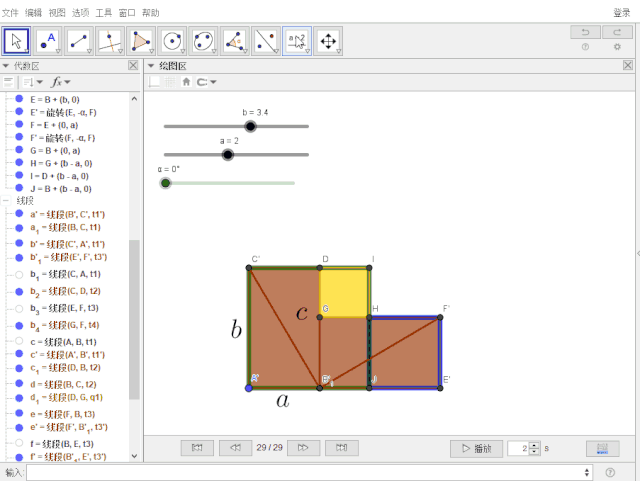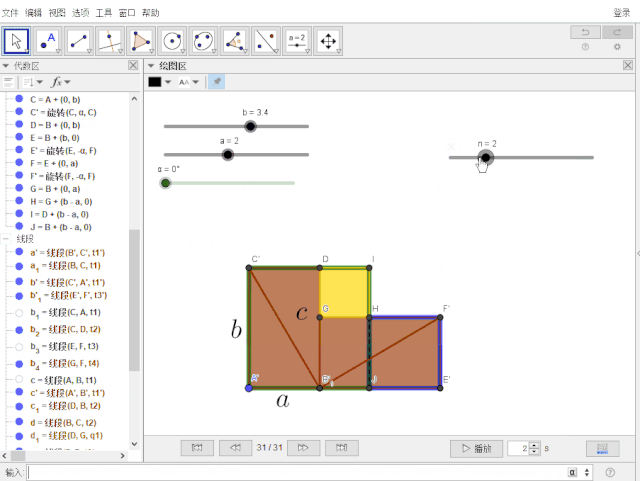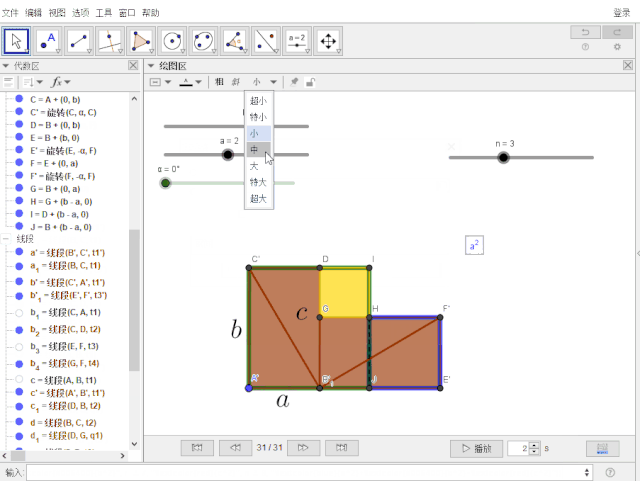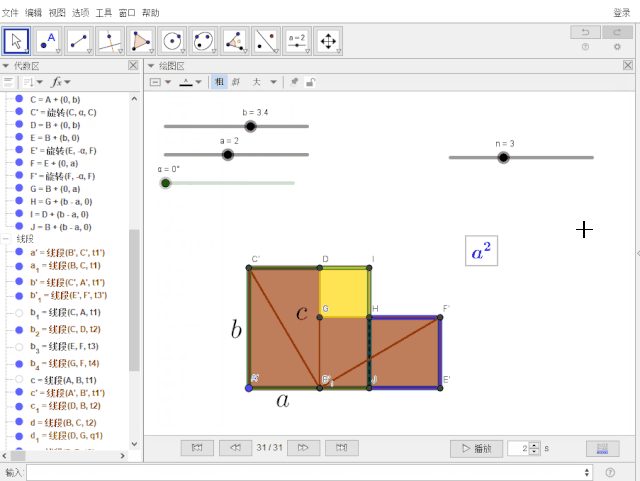
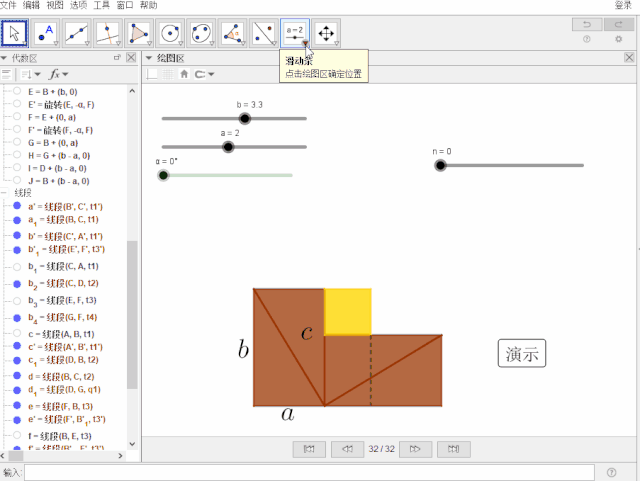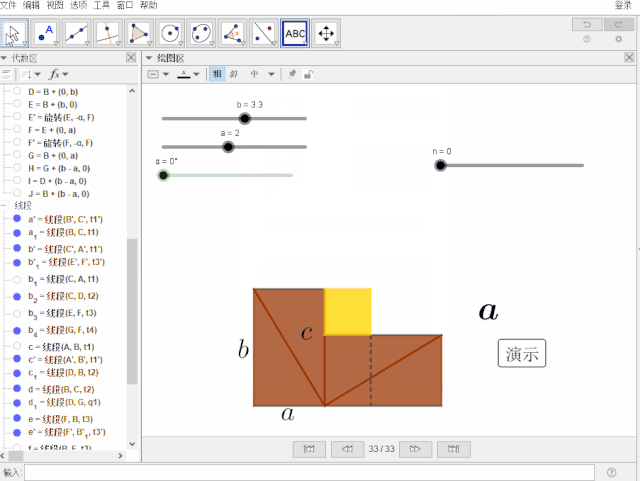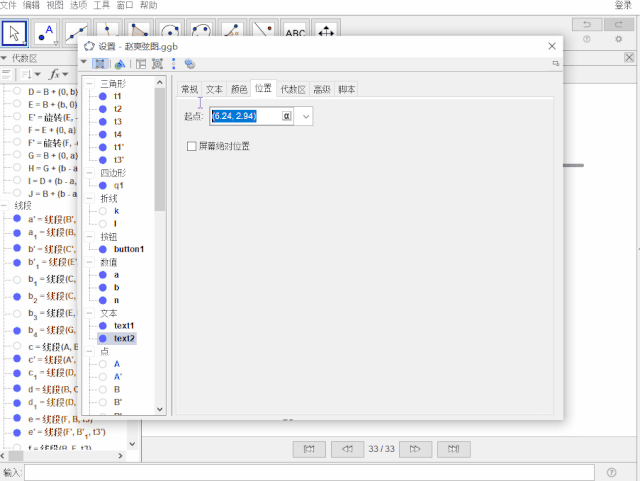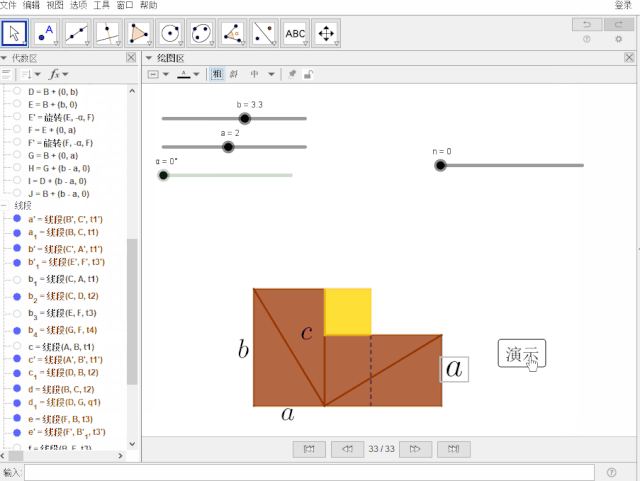
仅用一张动态的赵爽弦图就可明白如何证明勾股定理——请看用动态数学软件GeoGebra制作的效果图：

形象直观，可交互

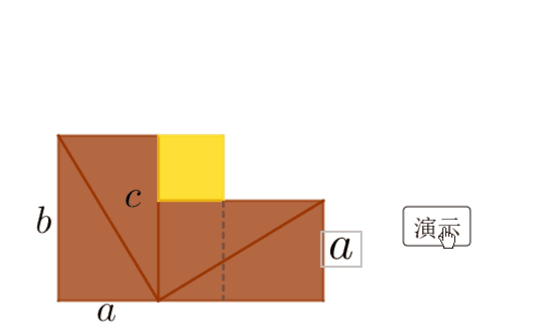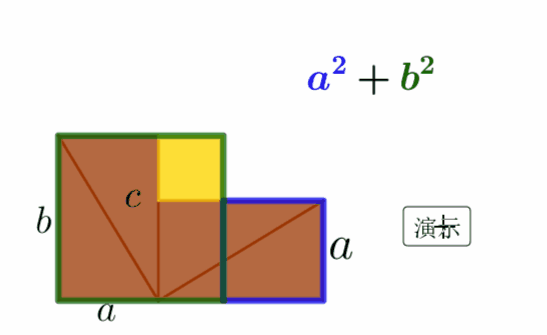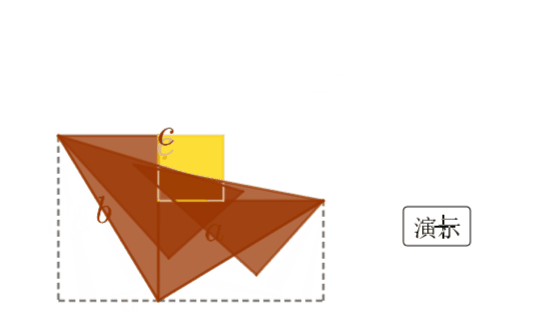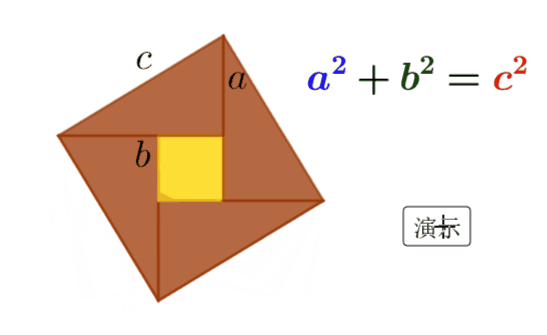
这是如何操作的呢？请往下看：

---

教程图 （关注公众号可获取word版）

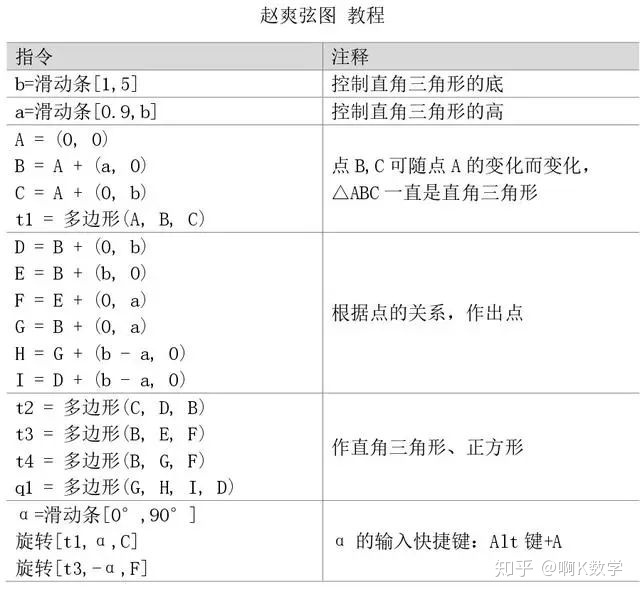
复制教程图中的指令，粘贴到数学软件GeoGebra的按钮脚本里。具体见下图。

粘贴到按钮脚本后——具体操作

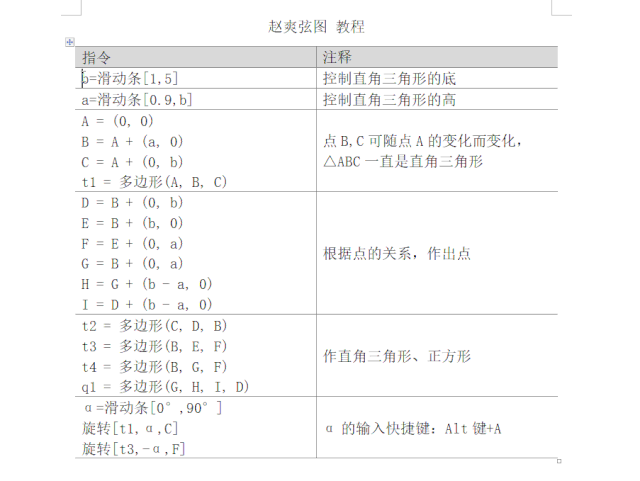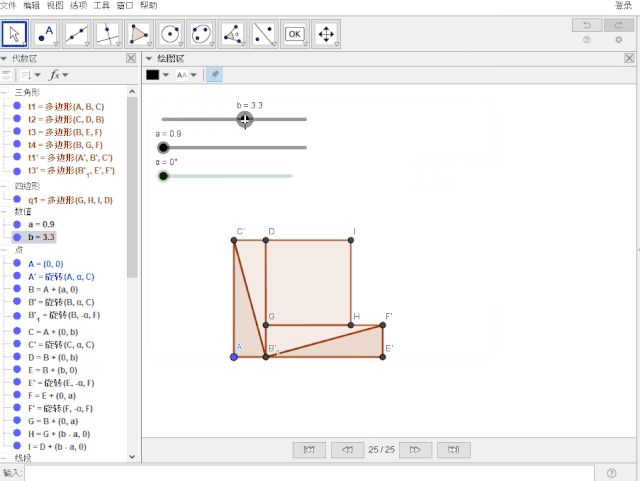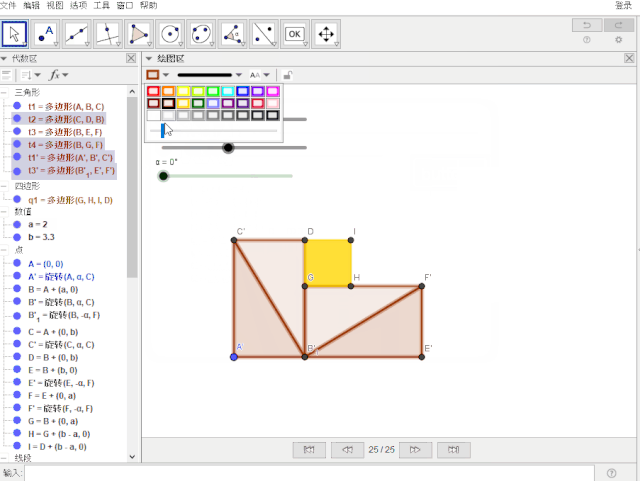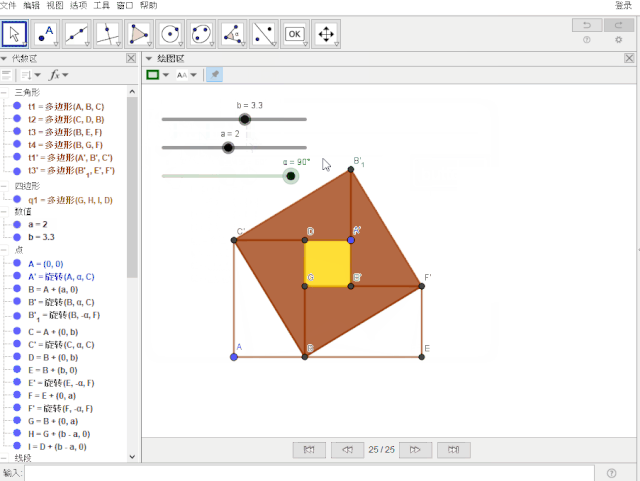
-----------------------啊K的手动分割线--------------------

• 这一操作是走了捷径的。
• 具体的分步操作请见动态的赵爽弦图（简易版）。

温馨提示：需输入的内容，可复制粘贴。

-------------------手动分割线2：细节修饰-------------------

设置线段颜色、线型、显示条件

进入线段c,b1,f,b3的属性——高级——显示条件，输入：α!= 0° && α != 90°

α!= 0° && α != 90° 即 α ≠0° 且α ≠ 90°

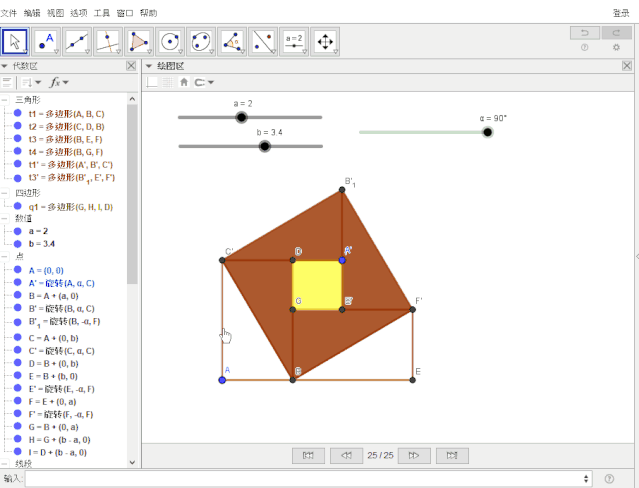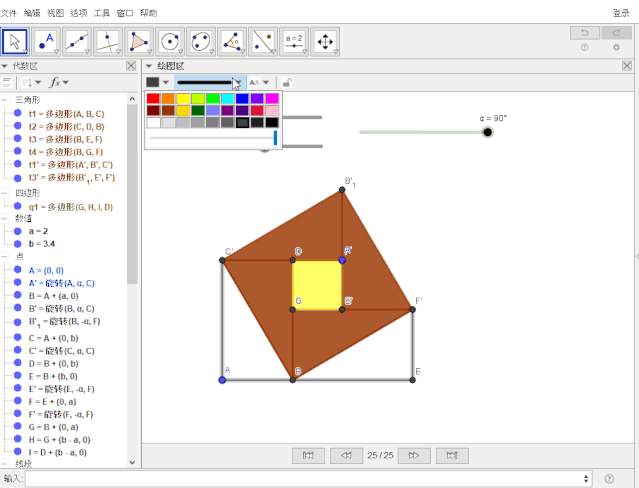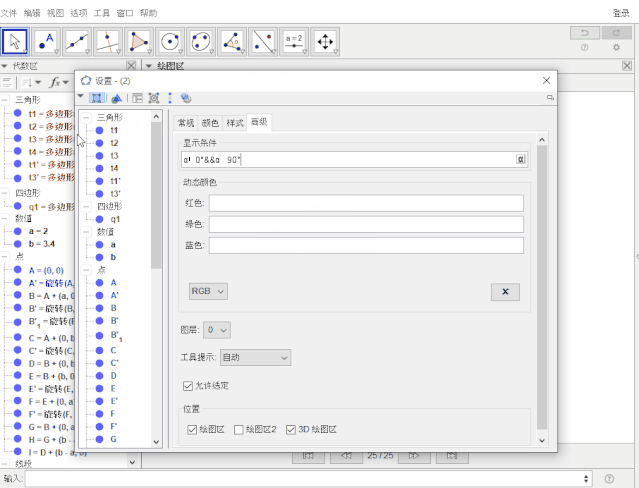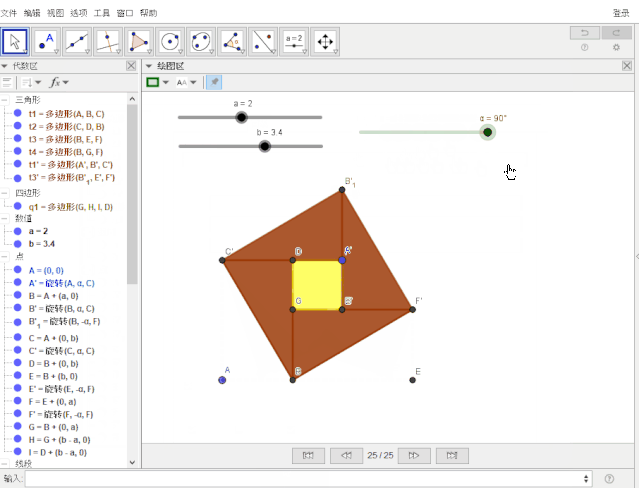
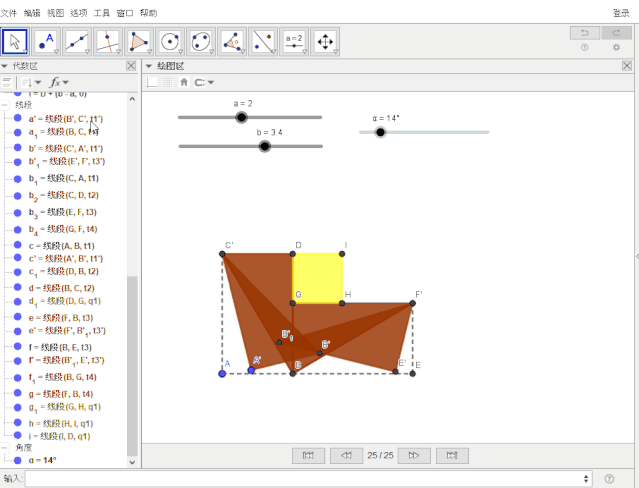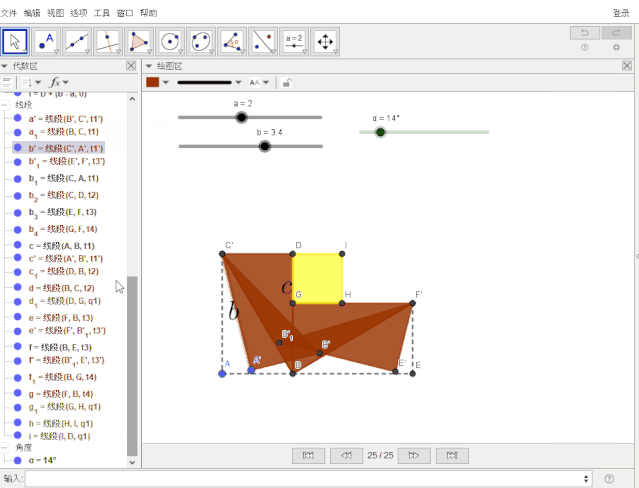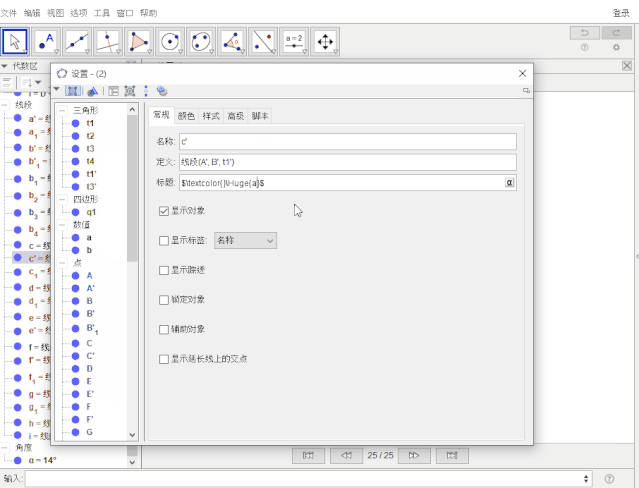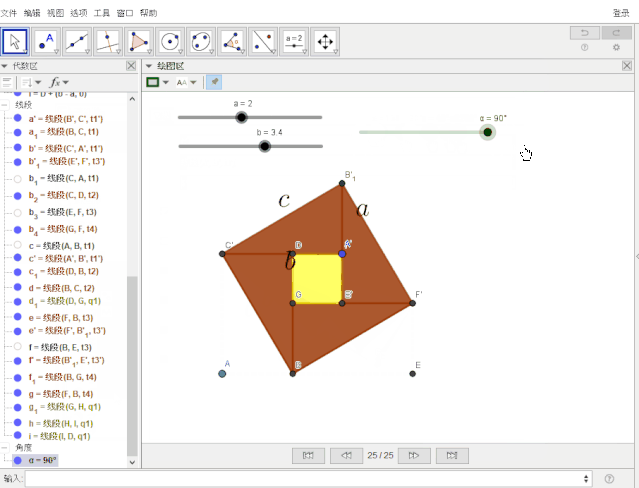
设置t1'三条边的标题：

1. $textcolor{}Huge{a}$
2. $textcolor{}Huge{b}$
3. $textcolor{}Huge{c}$

【快速找t1'三边:线段指令以 t1' ) 结尾】

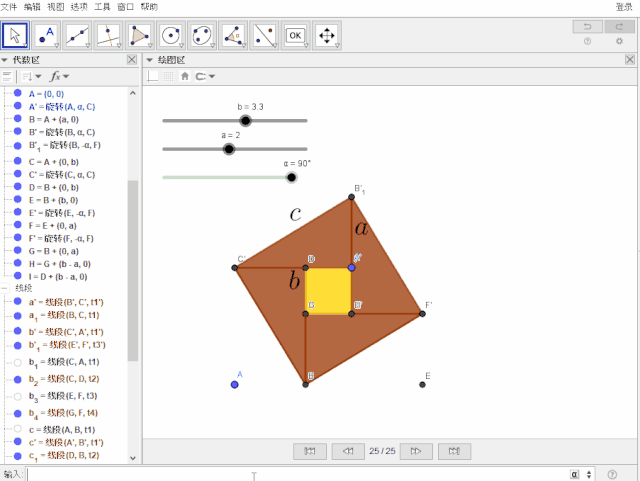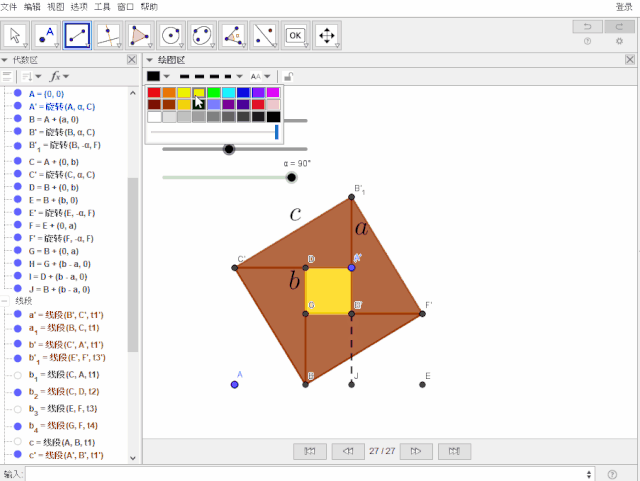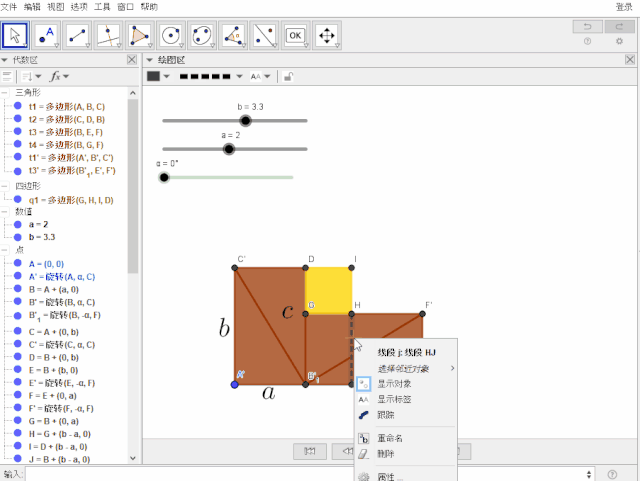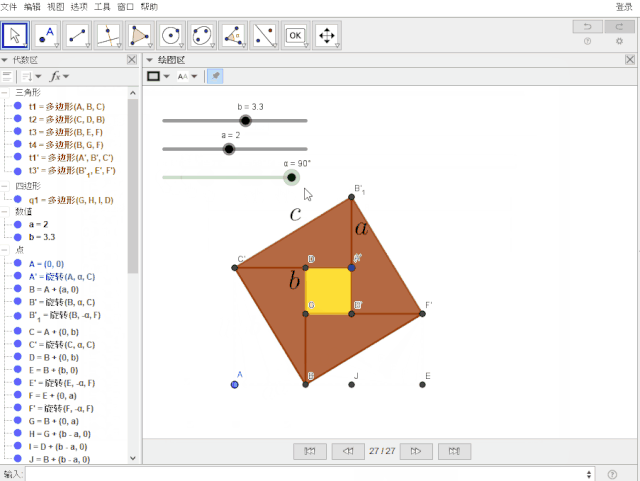
为使两个正方形更明显，作辅助线

J = B + (b - a, 0) , j = 线段(H, J)

设置线段 j为银灰色，线型为短划线，显示条件：α== 0°

简单点，到这里，只要隐藏所有点就行了

可以一步一步显示的重点来啦！

文字与按钮

1.分别输入指令: k = 折线(H, J, E, F, H) , l = 折线(C, A, J, I, C)，且设置线型与颜色

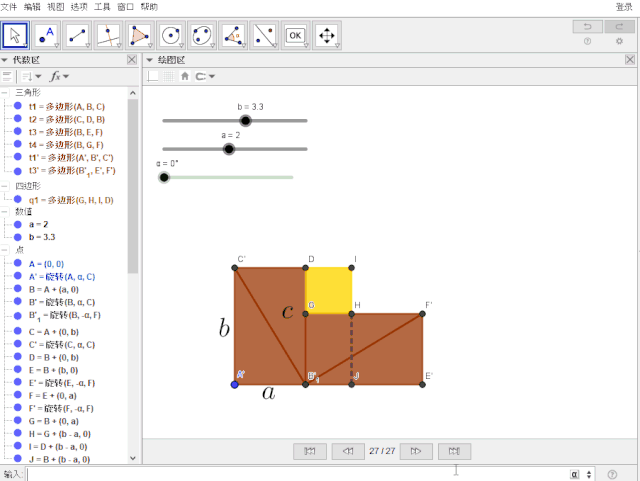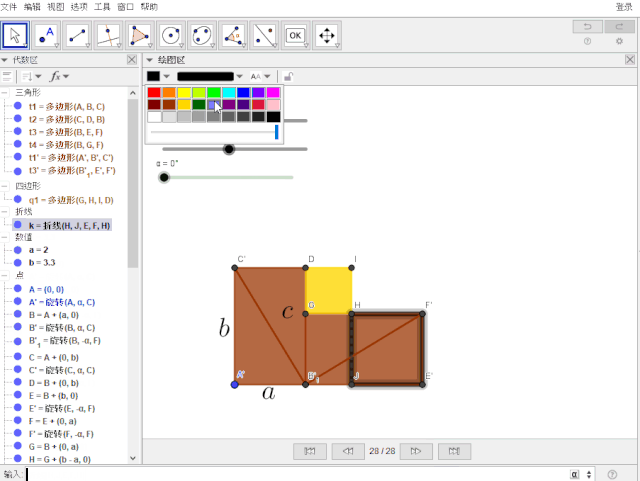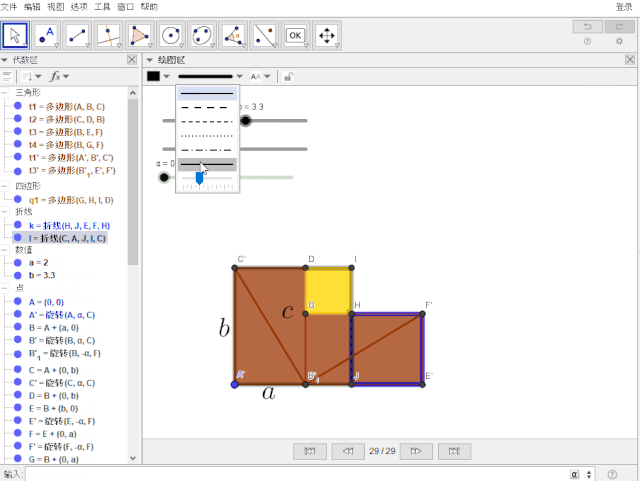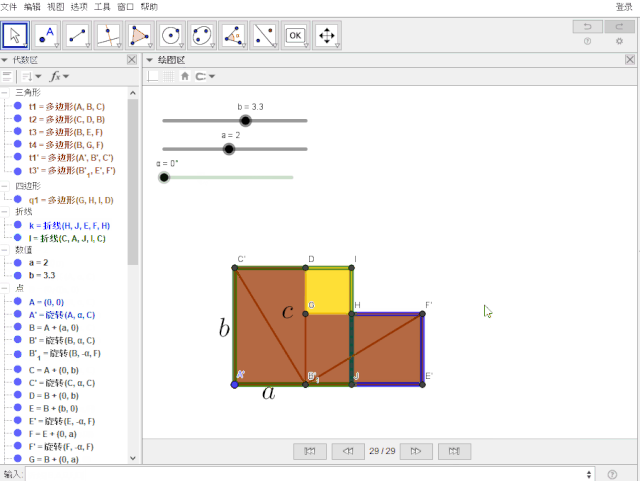
2.“重中之重”：

建立整数滑动条n【用来控制逐步显示】，输入指令【整段复制】：

text1 = 公式文本(如果(3 ≤ n < 5, "textcolor{blue}{a^2}", n ≟ 5, "textcolor{blue}{a^2}+textcolor{#006400}{b^2}", n ≟ 7, "textcolor{red}{c^2}", n ≟ 8, "textcolor{blue}{a^2}+textcolor{#006400}{b^2}=textcolor{red}{c^2}"))

n=滑动条[0,8,1]

n=滑动条[0,8,1]

3.“重中之重”：

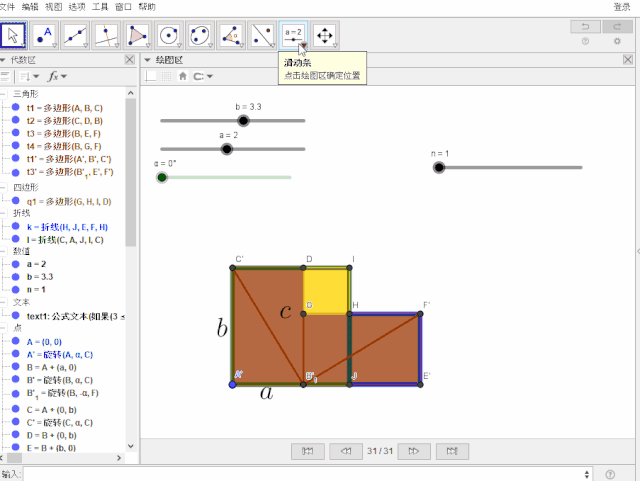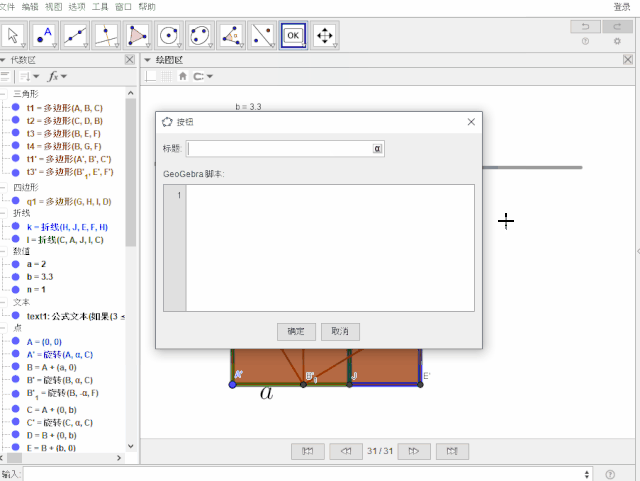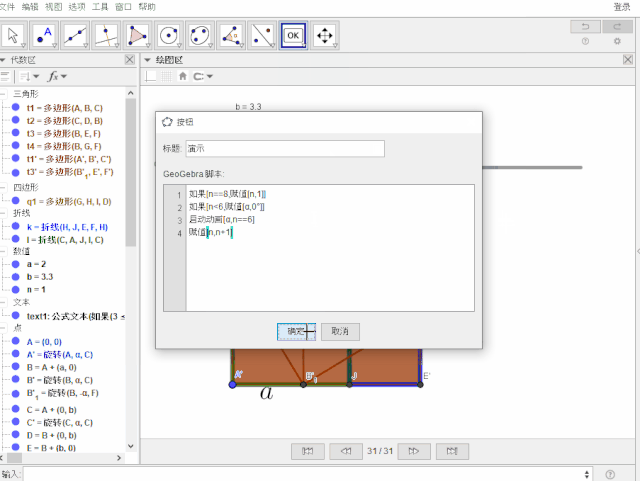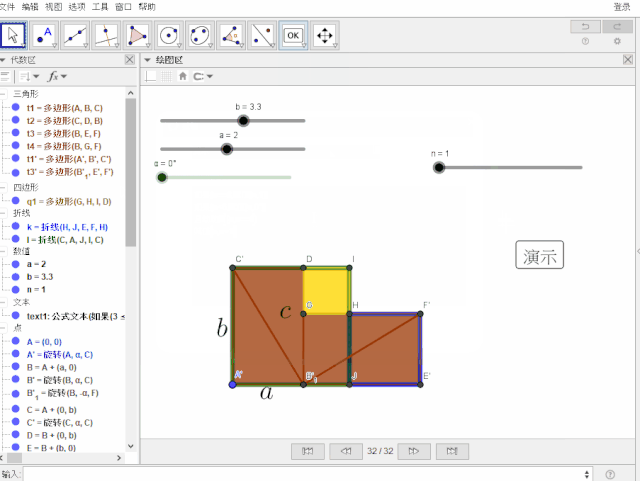
创建按钮，标题为：演示，脚本为【整段复制】：

如果[n==8,赋值[n,0]]

赋值[n,n+1]

如果[n<6,赋值[α,0°]]

启动动画[α,n==6]

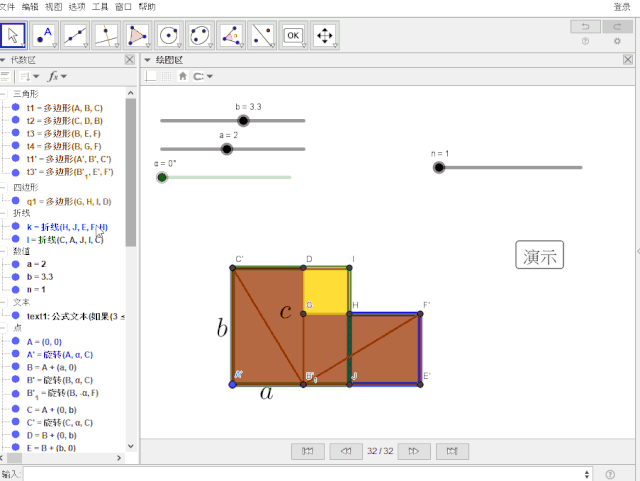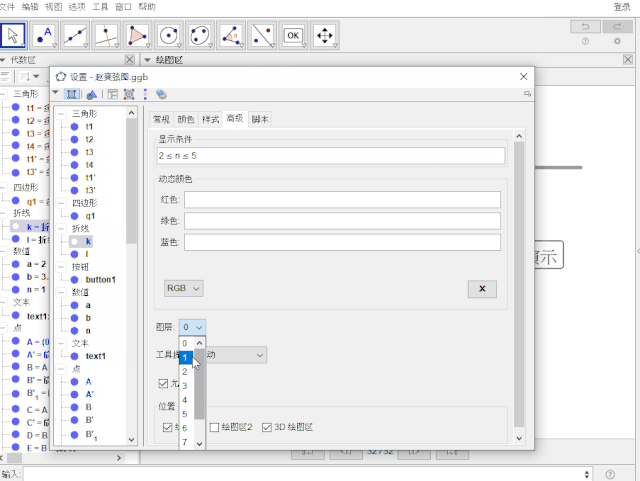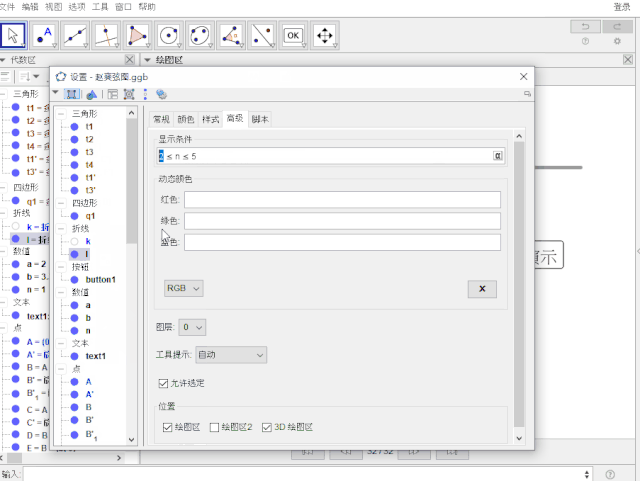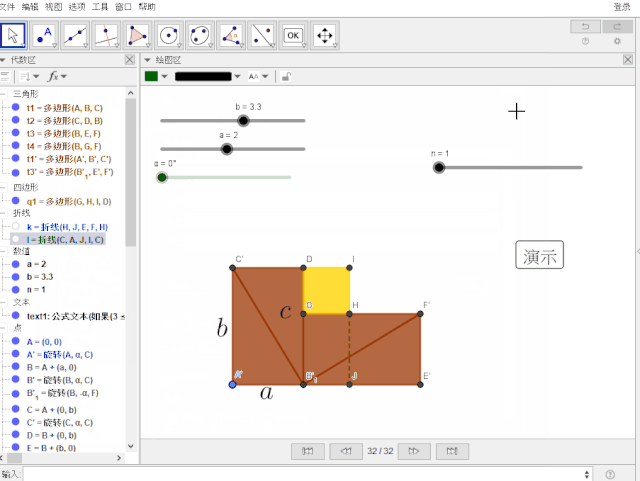
4.“重中之重”：

设置 k , l 的显示条件分别为：2 ≤ n ≤ 5 , 4 ≤ n ≤ 5；图层：都是1

5.设置α的速度为：5 ；隐藏所有点

【隐藏/显示快捷键：Ctrl键+G】

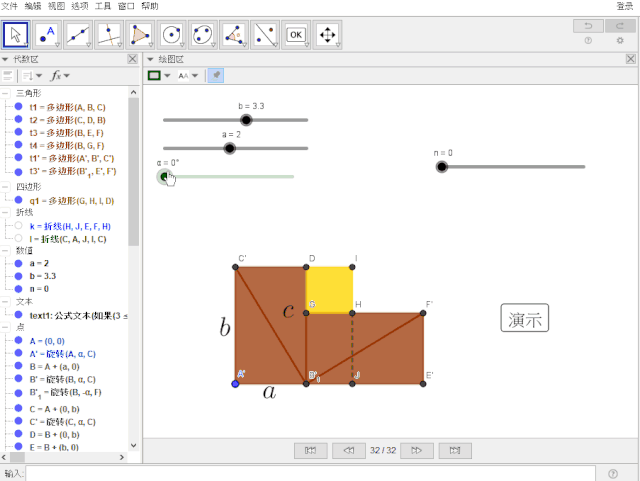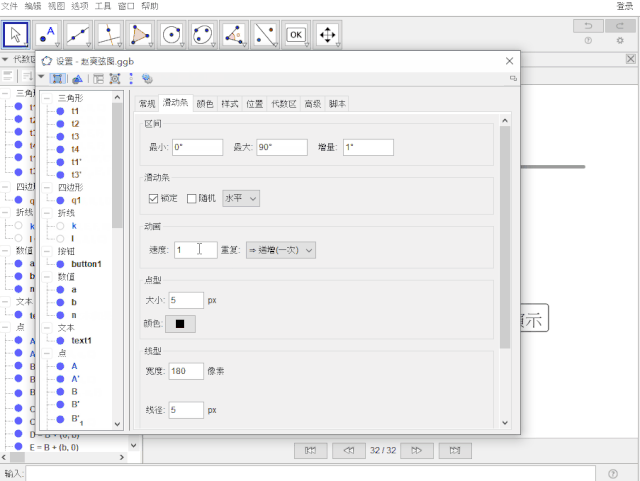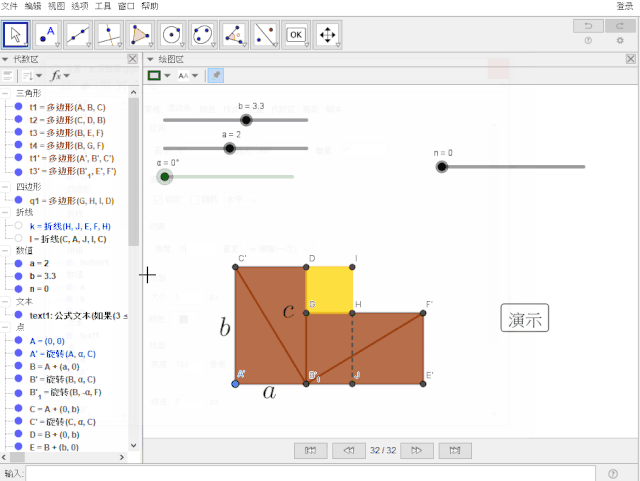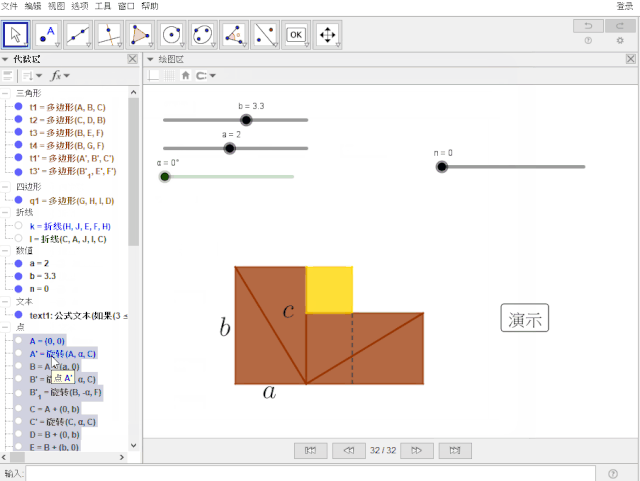
恭喜你！大功告成！

单击演示按钮，看看效果吧！

如需word版教程，请关注公众号GeoGebra数学（回复赵爽弦图即可获取）。

word版教程——部分截图

---

感谢提醒，现给小正方形标示边长。

边长a的显示

创建文本：Huge{a} ，显示条件为：n < 6 ，位置：中点(b_3)