求解出能被5整除的正整数的乘积_关于一个不定方程(特殊丢番图方程)的求解

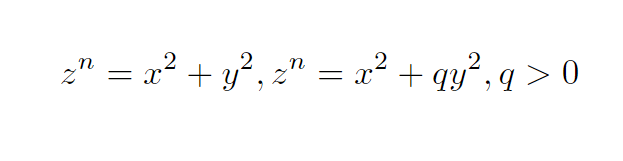
丢番图方程又被称作是不定方程、整系数多项式方程，是变量仅容许是整数的多项式等式；即形式如下的方程

其中所有的a,b,c均是整数，若其中能找到一组整数解使得方程成立，那么就称之有整数解。

本小结是讨论一个非常特殊的丢番图方程。这个问题最初的想法是在求解方程

时候出现的这个方程。在讨论这个方程之前，首先我们复习一下两个基本的概念:

二次剩余:当存在某个

,表达式

成立的时候,称

是模

的二次剩余;当对任意

不成立的时候,,称

是模

的非二次剩余.

Legebdre符号:设奇素数

,定义整变数

的函数

这非常容易理解这两个基本的定义，首先我们给出以下的一些定理

定理1 Legebdre符号有以下的性质

1. ;
2. ;
3. ;
4. 若
   ，则
   ；

这就是Legebdre符号常见的基本性质，容易证明。另外，还有一个重要的性质是

定理2 若

均为奇素数,

,那么就会有

我们基于以上的这些个性质来研究上述的一些定理。

首先我们得到这个引理

引理 设素数

,那么不定方程

有解的充要条件是

,即

是形如

的素数.

证明过程如下,首先证明上述引理的必要性:若上述不定方程有解

,则显然有

使用上述定理可以得到

根据定理1和定理2可以得到

所以这就会得到

,即

满足

.

充分性的证明有些复杂，是这样证明：由

可以得到同余方程

必定有解.

设

为其解.考虑集合

这个集合的元素个数等于

.由抽屉原则可以得到,必定有两组不同的

,使得

即有

这里

,

一定不全为零.由此以及

是上述同余方程的解,即得到

另一方面,由原方程可以得到

所以由上述两式可以得到有以下几种可能:

若

,则原方程必有解;若

,则必有

,所以就会有

,因而得到

,与

是奇质数矛盾;若

,则

,因而就会有

这样原方程也有解.证明完毕.

接下来就是最为重要的求解方程

的基本求解方法.这里我们叙述一下我们即将要求证的内容，即

定理3 设

,那么

成立的充要条件是存在

使得

以及

.

这是一道十足有些难度的证明题目.充分性的证明比较简单一些:

由

.我们使用复数来推导这一个结果.容易得到

所以这样就会得到

所以由这个等式以及

推导出

.由于

可以得到

即证明了充分性的成立.

必要性的证明就有些难度，这里使用到了数学归纳法的方法.主要的思想是从

的质因数分解的个数进行证明.

设等式

成立,这时候必定有

,故而

的任一素因素

一定是满足

进而推出必有

.这样对于

来说就会很容易地联系到上述证明的引理.现在设

表示

的素因素的个数(包括重数)规定

.下面用归纳法证明它的必要性.

初始情况:当

,即

时候,有

,这时候取

.故而必要性成立.

归纳假设:假设对

时候，

，必要性成立.

一般情况:那么当

时候,设

,

是素数,则

,所以这里就归结于对于

归纳假设的一般性质的证明.由于

满足

,由引理可以得到

并且满足条件

.由充分性证明可以得到

并且有

由此可以得到

下面证明:

和

两个数中有且仅有一个被

整除.容易得到

因而,

至少整除其中的一个数.假设

,则会得到

.由于

,所以

,这与

矛盾,假设错误.由于上式中被

整除必然被

整除.假设

,则可以得到

并且有

下面证明

.可以得到

消去

可以得到

由于

所以得到

,得到我们想要的结论.至此得到

归纳假设 可以得到,必有

使得

所以这样就会得到

这里取

.

为了推证方便，我们这里使用复数的方法来证明这一个问题.由上述的表达式可以得到

三个表达式可以得到

比较两边的虚部就可以推导出上述的表达式.容易得到

,从而推出

,证明完毕.

所以这样就可以得到方程

的正整数解所满足的条件

其中

.这样的一个方程笔者联想到的是一般形式的一个方程，即方程

的正整数解，这里要说明的是

,

.笔者看来

应该取素数最为合适，这样就会更为接近一般性质的解。不过我们可以先考虑方程

的基本解.在以上问题的讨论中，笔者发现复数表达的方法在求解这类不定方程解的问题中起到了至关重要的作用,所以说，对于以上的两个方程也是从复数的方法来求解方程整数解的形式.还是从最为简答的方程考虑，对以下的方程从特殊到一般的方法进行考虑

• n=3情况考虑方程
  .这里
  ,
  是一个质数.对于
  为合数的情形可以由
  为质数的情形所推导.所以我猜想
  满足的条件应该是
  这样为推导方便，使用复数来求解.所以这样就会得到

通过猜想的形式不难得到

对于

所满足的条件应该是

.

• 当s是一个的指数是一个奇数的方程
  .首先想到的是对于
  的解应该是
  的形式.为推导方便，我们依旧使用复数来求解，考虑复数

容易得到

同理有

现在设

所以这样就会得到以下的结果

.所以我们构造的表达式为以下的形式

这里的

应该满足的条件是

• 当s指数是一个奇数并且包含有系数q的方程
  .当然这里
  为了凸显一般的性质,这里选择质数的情况.依然使用复数的方式进行推导证明.这里的方法就是上一个方程中的
  替成为
  .那么构造以下的结果

构造

这样就会得到

,

应该满足的条件是

综合上述的三个归纳猜想，这样的几个猜想成立的话必须满足一定的前提条件.对于第一个和第三个猜想，则必须满足的条件是，对于特定的质数

，方程

存在正整数解.第二猜想来说，就是对于正整数

可以写成

的形式(不太严谨的说法).这些结论有待笔者进一步证明和探讨.

[1] 参考文献：《初等数论》，潘承洞，潘承彪