密码学原理与实践_【译】椭圆曲线密码学介绍之三：ECDH和ECDSA

原文：

Elliptic Curve Cryptography: ECDH and ECDSA​andrea.corbellini.name

本文是系列文章 ECC: a gentle introduction的第三篇。本文将会介绍两种具体的ECC算法：ECDH和ECDSA

领域参数（Domain parameters）

为了让我们的椭圆曲线算法能够真正的运行起来，首先我们需要一个定义在有限域中的椭圆曲线的循环子群，需要的参数如下：

• 一个质数
  用于描述有限域的大小
• 椭圆曲线方程的参数
  和
• 一个用于生成循环子群的基点
• 子群的阶数
• 子群的协因子
  （
  ，其中
  是椭圆曲线群的阶数）

这六个参数

联合起来定义了一种ECC算法所用到的椭圆曲线。

随机曲线（Random curves）

离散对数问题是“困难”的，这一陈述并不总是正确。事实上一些特定参数的椭圆曲线上的离散对数问题是很“容易”的，这使得一些带有特殊目的的算法可以有效地解决这些离散对数问题。举例来说，所有满足

（这意味着有限域的阶数和椭圆曲线群的阶数相等）的椭圆曲线都是不安全的，存在一种算法可以在多项式时间内解开这类椭圆曲线上的离散对数问题。

现在假设提供我提供了一组椭圆曲线的领域参数，那么这就存在一种可能：我私下里发现了一类新的安全性较差的曲线，这类曲线从未被公开过，我还自己实现了一种针对这类曲线的离散对数问题的快速解法。那么我该如何让其他人相信，我不是有意地构造出这条曲线呢？我该如何向你保证，我给出的这条曲线是安全的呢？

为了解决上述问题，我们需要一个额外的参数

，我们称之为随机种子。这是一个随机的数字，用于生成参数

或者基点

。这些参数都是由

的哈希值生成的，我们知道，哈希函数的计算很简单，但是我们很难通过哈希值反推出函数输入。

如何从S生成随机曲线：S的哈希值用于计算曲线的不同参数。

如果我们想作弊，并试图从特定的参数中构造一个S，我们必须解决一个“难题”：逆哈希

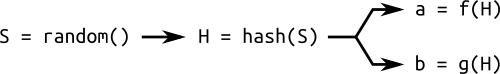
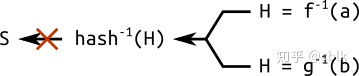
一条通过随机种子生成的椭圆曲线被认为是可验证随机的。这种基于哈希函数来生成参数的原则通常称之为"nothing up my sleeve"，这在密码学中是十分常用的方法。

这个技巧可以为椭圆曲线的安全性给与一定的保证，至少这条曲线不是有人特意构造出来，然后在其中隐藏了什么不为人知的漏洞。事实上，如果我提供了一个随机种子和对应的参数，这意味着我不能随意地选择参数

，那么其他人就应该

比较确定这条曲线不能被我用于”特殊目的“的攻击。在下一篇文章中，作者将介绍为什么这里要说是”比较确定“，而不是完全保证。

ANSI X9.62中描述了一种用于生成和检查随机曲线的标准化算法，该算法基于SHA-1。如果你还想了解得更多，你可以看一下这个算法（请在文档中查找"Verifiably Random Curves and Base Point Generators"这一节）

作者写了一个Python脚本用来检验OpenSSL当前附带的所有随机曲线。读者可以自己运行一下。

椭圆曲线密码学（Elliptic Curve Cryptography）

用了这么多篇幅，现在终于要到我们的正题了，我们开始正式介绍ECC算法的细节：

1. 从
   中随机选择一个整数
   作为私钥（
   是循环子群的阶数）
2. 计算公钥