均值滤波计算_快速掌握卡尔曼滤波器 - 边学边用

卡尔曼滤波器 (Kalman Filter) 是一种常见又高效的滤波器，可以用在控制、滤波、信号融合等方面，是热门行业里必备的一个工具，例如自动驾驶，计算机视觉等领域。这期文章不是来推导卡尔曼滤波，而是帮助大家快速学会卡尔曼滤波器并了解其在目标追踪或数据融合领域的应用。

---

在我之前的文章中有介绍过贝叶斯理论和贝叶斯递归滤波(可以参考一下链接），

缪天磊：贝叶斯递归滤波​zhuanlan.zhihu.com

而卡尔曼滤波器其实就是一种特殊的贝叶斯递归滤波器，因此也具有和贝叶斯递归滤波器一样的作用，就是用来迭代地估计一些不容易被直接计算或者测量到的参数，例如目标追踪里目标的真实状态。

这里我先介绍两个参数，

是目标的真实状态，

是测量结果。我举一个具体的例子大家肯定就明白，一辆汽车在路上匀速直线行驶，限速50，而汽车的速度就刚好是50码（在危险的边缘试探），假设路上有测速监控，并且随时都能测出速度，测出的结果是52码。这里50码就是汽车的真实状态，52码就是用监控测出来的测量结果。我们目的就是在只有52码这个测量结果的时候去估计汽车到底开的多少码，如果直接根据这个52码就说它超速显然结果是错了。

这个时候就抛出了我们遇到的问题，如果监控测到52码，这个汽车到底超没超速？或者说监控测到多少码的时候才能说明汽车超速了？这其实就是一个典型可以应用贝叶斯理论的例子，用我们已知的测量去估计真实状态。假设我们知道测量模型，例如这个监控测到速度常年高于真实速度2码，我们又把司机抓来了盘问，司机说了他真的开的50码，那么我们是不是可以推测得到他确实没有超速。

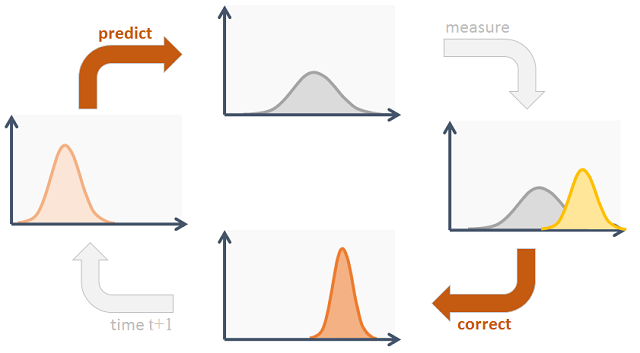
上面这个例子其实是忽略了时序的，而大多数时候目标的状态和测量的结果都会随着时间的变化而变化。这也是为什么要用贝叶斯递归滤波，回顾一下贝叶斯滤波器的两个步骤：

预测步：根据运动模型和之前的信息来预测新的时刻目标的状态

更新步：根据测量模型和刚刚的预测结果来更新目标的状态

公式虽然看着复杂，但是让我们套用之前测车速的例子看看：假设上一秒我们知道车速刚好是50码，并且司机告诉你，他一个老司机开了20年车，绝对开的是匀速（这就是运动模型），分毫不差，那么我们就根据这两个信息预测出这一秒车速还是50码；同时，测速监控测到车速这一秒车速是52码，而且我们也知道这个测速监控测量结果常常高2码(这就是测量模型)，那么根据测量模型，这一秒的测量结果和之前的预测，我们得出结论，车速确实是50码。当然这里的结论车速也只是一个估计值，但已经算是比较准确了。

有了上面的例子做支撑以后，下面开始正题：卡尔曼滤波器。观察预测步的公式，我们会发现里面有个积分，而在实际计算中，积分运算其实没有这么容易，而且会增长运算时间。而卡尔曼滤波器第一个作用就是给出了处理这个积分的一种方法。当然使用卡尔曼滤波器有个前提，即模型都必须是线性高斯模型(不了解高斯分布的同学可以参考这篇文章：https://zhuanlan.zhihu.com/p/50738318)，因为它的推导都是基于这个假设的。我们先跳过推导，直接看结论：

假设我们有以下运动和测量模型：

A叫做转移矩阵，有了它我们就可以根据上个时刻的状态推导此时的状态，q是运动模型里的误差（更广义的情况下叫做过程噪声）且服从均值为

，方差为Q的高斯分布。类似的，H是测量矩阵，用来从真实状态推出测量结果，当然也可以用来反推，r是测量噪声且服从均值为

方差为R的高斯分布。

根据上面的例子，目标状态只考虑速度，且假设A和H都等于1，为了帮助理解，运动和测量模型改写为以下：

这样运动模型就是这一秒的速度等于上一秒速度加上噪声(即一些不确定性，司机告诉你匀速就真的匀速吗？)，测量模型等于这一秒的速度加上测量噪声(这个传感器本身就有一些问题)。问题可以转变为我们知道了z，那么真实速度v到底是多少？这里直接先给出结论：卡尔曼滤波直接根据假设模型都是线性高斯分布，把上面的预测和更新步骤改成了均值和方差的预测和更新，这样不用再积分求概率密度了，直接得到高斯分布的均值和方差，从而得到了完整的分布情况。公式如下：

预测步：

更新步

其中

这样，之前的积分运算，现在就变成了一个简单的矩阵运算，程序上非常容易实现。而卡尔曼滤波的厉害之处不单单只是这样，观察更新步的公式，新的时刻的均值等于预测均值加上卡尔曼增益与更新量的积，而预测均值是根据运动模型得到，更新量是更根据测量结果和测量模型计算得到的，那么我们可以发现，新的均值其实就是结合了运动模型和预测模型。并且如果测量结果更接近真实值，那么卡尔曼增益的值就会变大，如果预测结果更接近真实值，那么卡尔曼增益就减少，换句话说，哪个模型更准确就分配更多的重量给这个模型。这就让迭代过程变成了自回归过程，因此卡尔曼滤波器是一个自回归滤波器，它会根据测量值和预测值哪个更接近真实值，来调整运动和测量模型的权重。

根据上面的车速的例子，带入各项到卡尔曼滤波的计算过程中(此处更新量为0)，我们最终得到真实车速是一个均值为50码，方差为(Q x R)/(Q+R)，假设Q =1, R =4, 方差为0.8，我们就可以算出真实车速的分布。

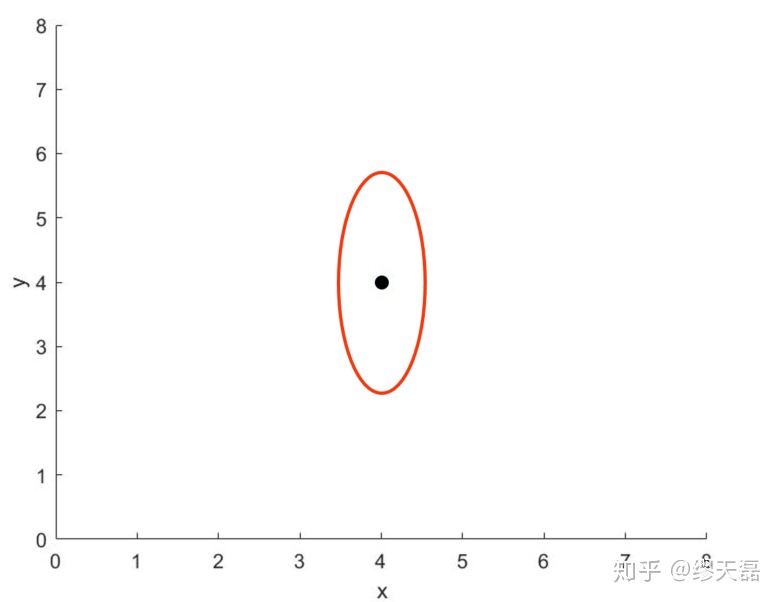
下面我用一个2d坐标的例子来帮助大家更好理解，这次考虑一个机器人，初始的位置是高斯分布且如图，均值在[4, 4]，协方差为红圈，用来描述位置的不确定性，即有可能在这个范围里变化，越靠近均值概率越大

然后运用卡尔曼滤波方法，第一步根据运动模型预测，这里我们简单假设运动模型是横向速度为1m/s，纵向为0的简单运动模型

预测步结果变成了均值为[5, 4]，协方差如绿圈，比原来更大了，说明不确定性比原来更大了，因为运动模型有噪声，两者相加变得更大了。

第二步，根据测量到的结果再次更新，假设测量到结果为[5.7, 5.4]：

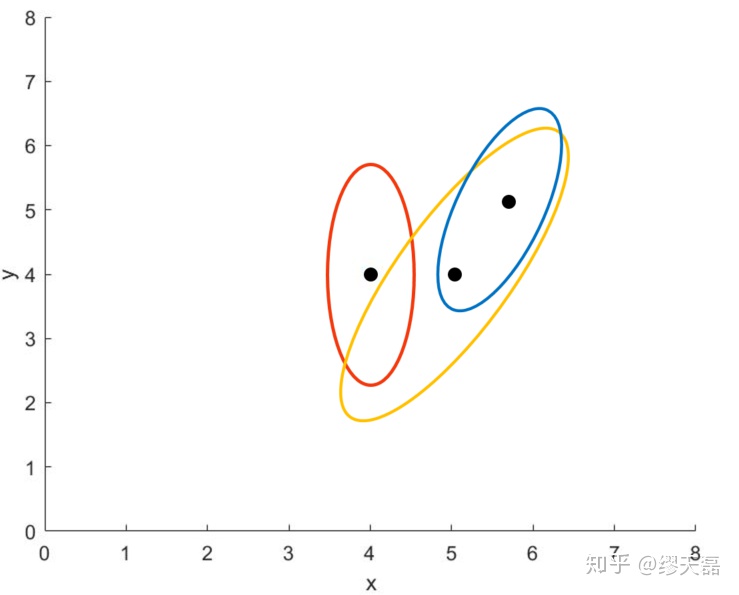
更新结果为均值为[5.5, 5.2]，协方差为蓝圈。以此我们就完成一次卡尔曼滤波的计算了，新的结果就是更新结果。这样随着时间，对于目标状态的估计始终能根据新的测量值和基于运动模型的预测值，调整我们对两个模型的信任程度，自动达到一种相对最优的状态，这就是卡尔曼滤波器的作用了。

到这里我相信大家对于卡尔曼滤波器的作用和特点已经有了大致的了解，有兴趣也可以自己看一下卡尔曼滤波器的推导。