目前较为常见的参数估计方法有极大似然估计、最大后验概率估计、贝叶斯估计。以下以抛硬币为例比较三种参数估计方法。

极大似然估计:根据样本的概率分布,写出样本的联合概率似然函数,通过最大化似然函数,得到参数估计值。只基于样本信息。
步骤:(1)确定似然函数
(2)将似然函数转换为对数似然函数
(3)求对数似然函数的最大值(求导,解似然方程)
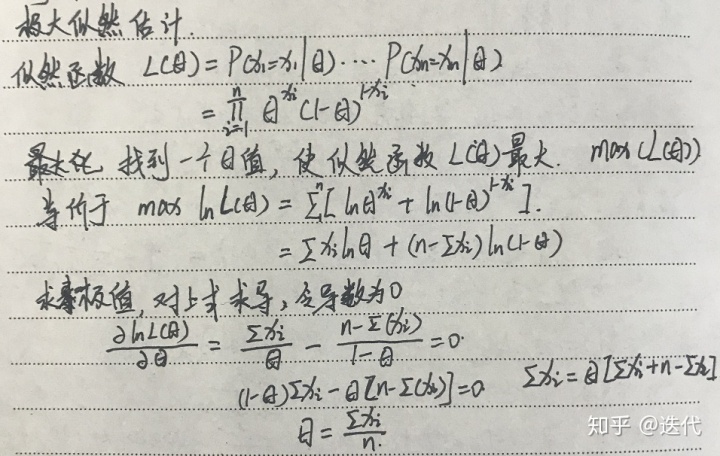
最大后验概率估计与贝叶斯估计都需要用到先验概率,两者的区别在于:最大后验概率分布认为
 本文介绍了参数估计的三种方法:极大似然估计、最大后验概率估计和贝叶斯估计。通过抛硬币的例子,展示了如何运用这些方法进行参数估计。最大后验概率估计在考虑先验概率的同时,比极大似然估计更稳健,尤其在小样本情况下。而贝叶斯估计则进一步结合了先验信息,当样本数量增加时,其结果趋向于极大似然估计。
本文介绍了参数估计的三种方法:极大似然估计、最大后验概率估计和贝叶斯估计。通过抛硬币的例子,展示了如何运用这些方法进行参数估计。最大后验概率估计在考虑先验概率的同时,比极大似然估计更稳健,尤其在小样本情况下。而贝叶斯估计则进一步结合了先验信息,当样本数量增加时,其结果趋向于极大似然估计。
目前较为常见的参数估计方法有极大似然估计、最大后验概率估计、贝叶斯估计。以下以抛硬币为例比较三种参数估计方法。

极大似然估计:根据样本的概率分布,写出样本的联合概率似然函数,通过最大化似然函数,得到参数估计值。只基于样本信息。
步骤:(1)确定似然函数
(2)将似然函数转换为对数似然函数
(3)求对数似然函数的最大值(求导,解似然方程)
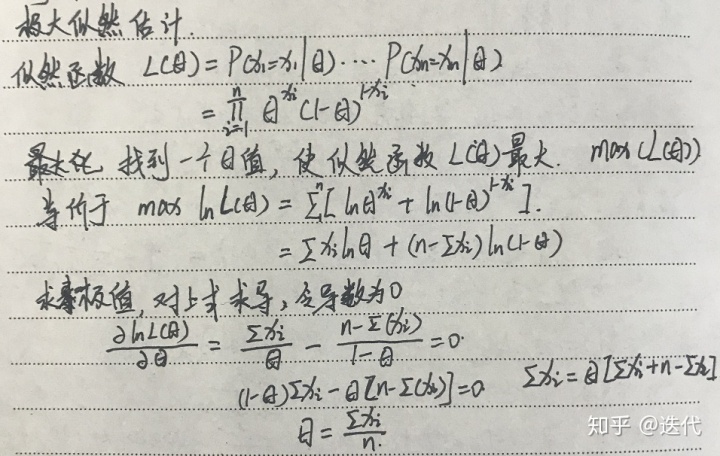
最大后验概率估计与贝叶斯估计都需要用到先验概率,两者的区别在于:最大后验概率分布认为











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


