概率论g是什么分布_概率论3「学生成绩转化」为正态分布和偏态分布的方法

来自我的概率论课程项目3，由于是小组作业，我在这里主要分享我个人做的工作（其实也很完整）

这个项目3分为成绩计算和统计分析两部分，本文是第一部分成绩计算，第二部分传送门：

低薪小明：概率论3「学生成绩分析」​zhuanlan.zhihu.com

老师的任务要求：

老师在临近期末时对全班学生平时表现进行了量化评分，评分标准如下：

由于我校有要求最终的成绩成类似正态分布，所以需要进行这一步转化。所以老师同时布置给学生们一个大作业（就是本项目）：将全班学生平时成绩计算出并找合适的分布模型拟合，并在excel中实现自动计算和转化。

本文使用了了3种拟合模型：正态分布、正偏态分布、负偏态分布。根据学生成绩分布情况的不同和老师希望学生成绩修正后的结果选择不同的模型。

一、正偏态分布

平均值在最高值左侧（小）

来自百度百科

正偏态_百度百科

1. 合理性

将原始成绩在其总体成绩中的相对位次比率当作从负无穷到量化成绩之间的 累积概率，通过相对位次比率间接对原始成绩进行处理，以非线性的方式调 整原始成绩的分布状态.因为位次比率是个纯量，所以这些纯量间具有可比 性，由位次比率转换后得到的量化成绩也具有可比性。

2. 计算方法

参考文献：考试成绩转换成偏态分布量化成绩的算法.李光兴,余洪琼. [J].高师理科刊,2020,40(01):22-26+31.

来自我组的ppt展示

3. 以本班同学为例计算（全部excel实现）

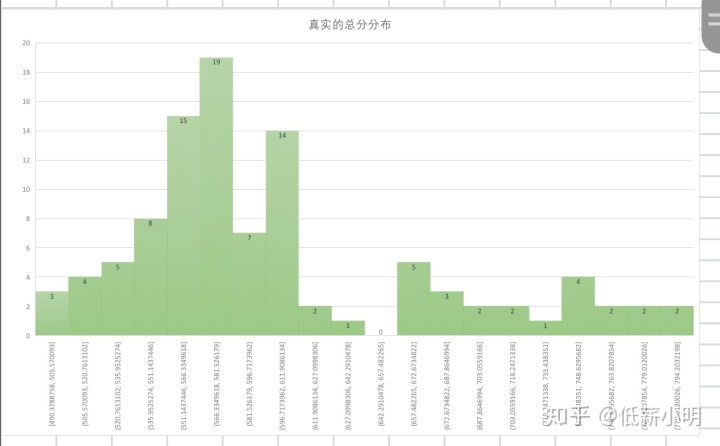
转化前成绩分布图：

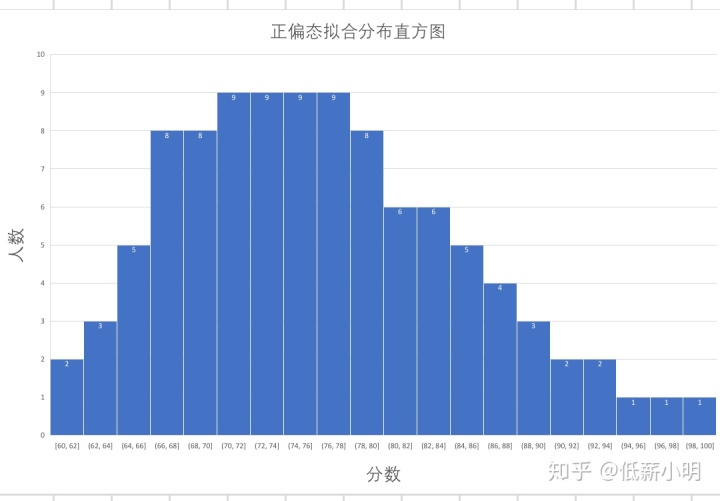
转化后成绩分布图：

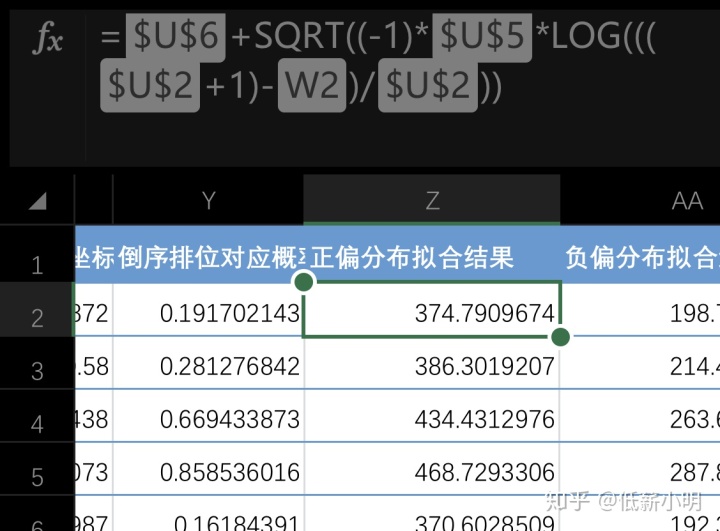
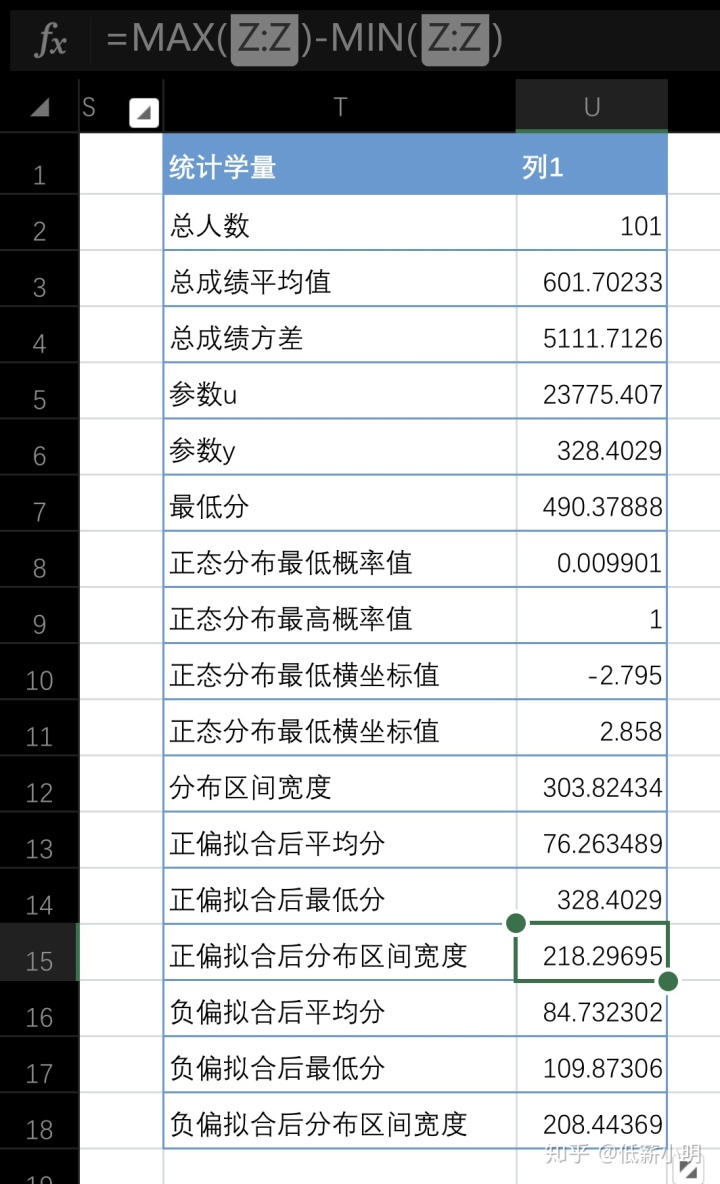
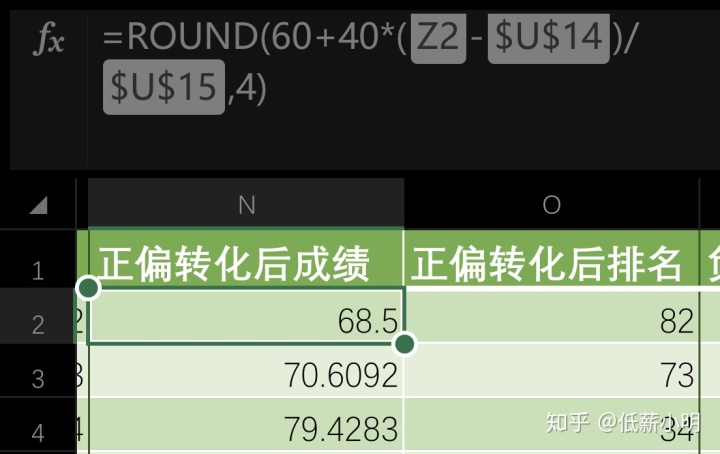
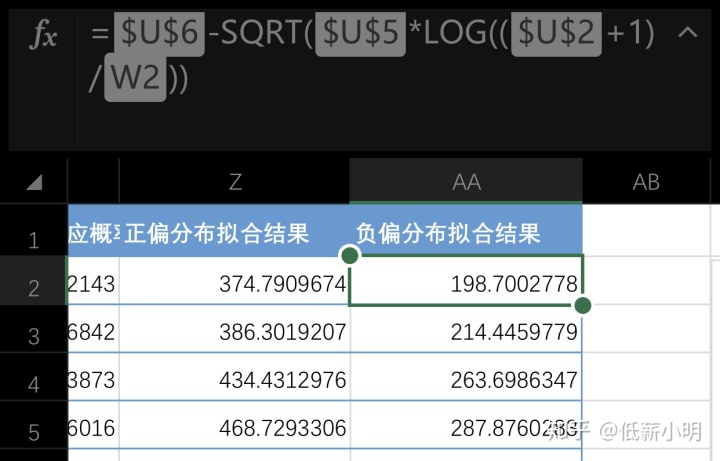
excel计算重点公式：

二、负偏态分布

负偏态_百度百科

1. 合理性

除非学生成绩真长这样，没什么合理性。如果老师希望高分的学生多一些可以采取这种转化。

2. 计算方法：几乎完全同上

3. 举例（excel实现）

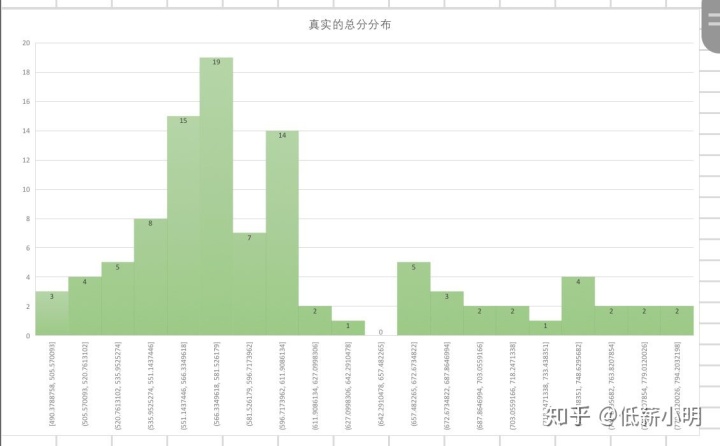
转换前：

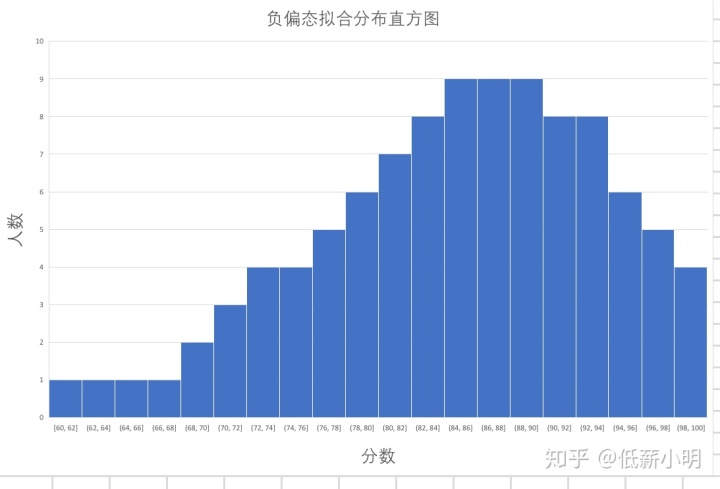
转换后：

excel重点计算公式：

三、正态分布

1. 合理性：

一般的考分换算方法为比例插值法，即将原始分 数由小到大排列，而后在设定好的区间内用数学 插值法转换分数。然而为了让转换后的分数符合 正态分布，我们引入了累积百分位，先将由原始 分数标准化成百分位，然后将百分位转化成一系 列“正态百分位”，最后再进行数学插值。

2. 计算方法

来自我组展示ppt

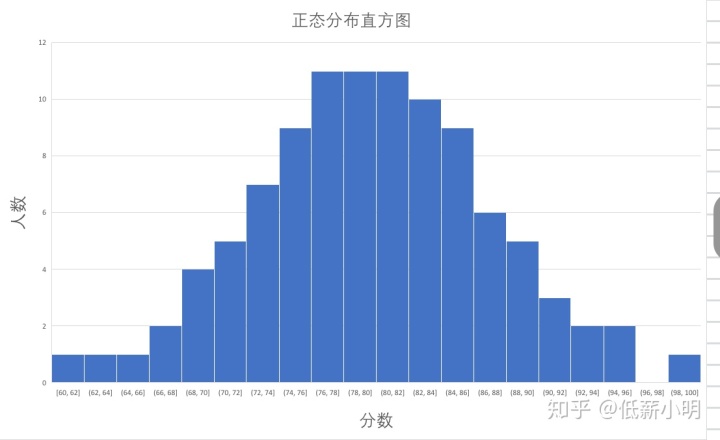
3. 举例展示

转化前：

转化后：

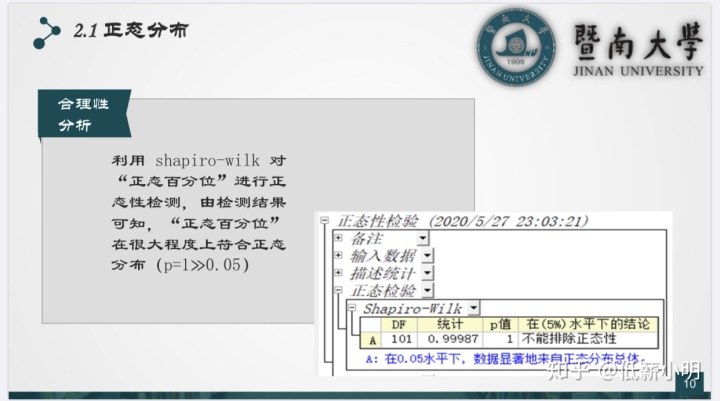
4. 正态检验

matlab代码

用于展示，方便理解，最后的实现是在excel中。

Excel关键公式

具体excel实现可以见下篇

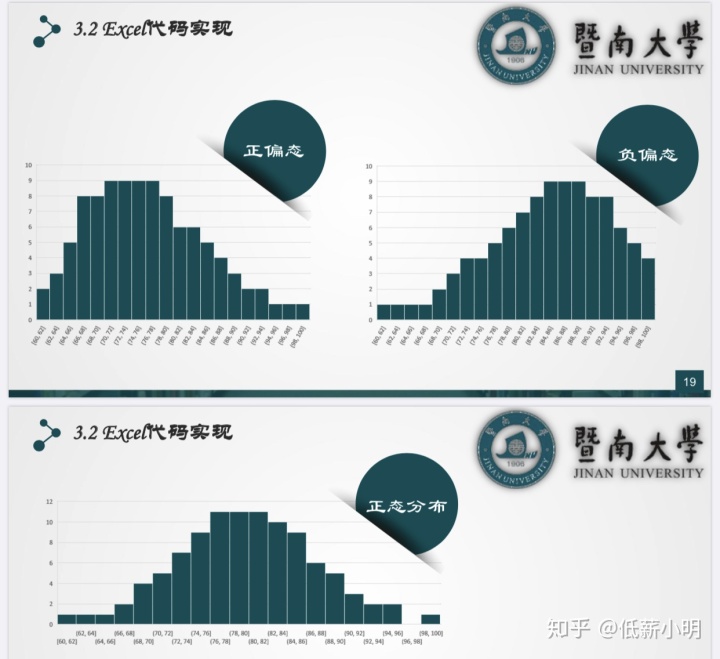
总结展示