世界上最难的视觉图_1+1=2的证明方法，为什么称为世界上最难的数学题？

1+1等于几，这几乎小学一年级都可以脱口而出的数学题，为什么证明这个关系成立，耗尽所有数学家的毕生心血，都无法去证明呢？

我们都知道，1+1=2，是最简单的数学公式，其次才有1+2=3，1+3=4.....，种种数学等式出来。可见1+1=2是所有数学公式的基础，也是数学这么学科的根本，关于这条等式，你知道？到现在都没人能够证明。

接下来为大家讲解下，这个公式有何难解之处。

1. 都说陈景润证明了(1+2)但是还没人能证明(1+1)。总觉得好奇。。
1+1＝2不是我们小学就知道的吗？
没经过证明我们怎么就在用了呢？
1+1＝2不是和1+2＝3一样的证明方法吗？

2. 首先你要知道。陈景润证明的是“哥德巴赫猜想”相关的问题。
哥德巴赫猜想是一个叫哥德巴赫的数学家提出的，大概是说：任何一个大于2的偶数都能分解成两个素数之和。
比方说8＝3+5，26＝19+5……
素数是指该数只能被1和它本身除尽。比方7，11，19。
现在这个命题还没有得到证明。但是通过计算机的高速运算，人们可以计算出直到很大很大的数字上，这个命题都是正确的。它应该就是正确的。
很早以前，外国人就证明了任何一个大于X(X应该不会很大)的偶数都能分解成一个素数与7个素数乘积的和。人们把这个表示成(1+7)
后来慢慢有人能证明一个大偶数能分解成一个素数与6个素数乘积的和(1+6)；一个素数与5个素数乘积的和(1+5)……。
再后来，我国的陈景润证明了任何一个大偶数都能分解成一个素数与2个素数乘积的和，这就是人们常说的(1+2)。比方18＝3(3*5)；30＝5+(5*5)。

3. 同理可证，要证明1+1=2，要用到要用皮亚诺公理才能证明，关于0的定义和1的定义。

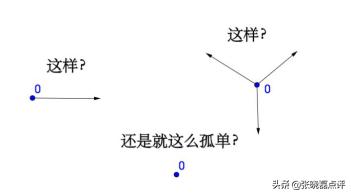
关于这一点的思考要充分，这本是一个非常自然的数，但在数学强调逻辑的里面，数字的开端无疑像宇宙大爆炸的基点一样。

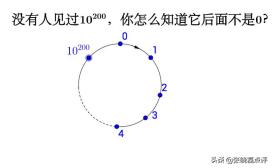
皮亚诺公理基本上雏形是有了：数字的开端都为零，两个零相加按照数学逻辑也会等于2。

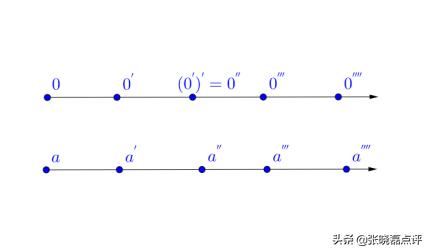
公理1：0是自然数。

公理2：每一个确定的自然数 ，都有一个确定的后继数 , 也是自然数。

公理3：0不是任何自然数的后继数。

公理4：不同的自然数有不同的后继数。

先证明这4条公理成立。

接下来开始证明1+1=2

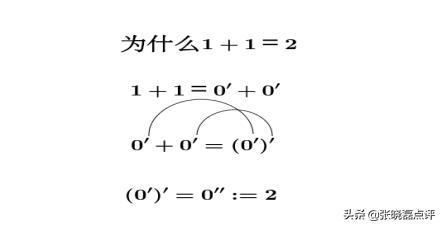
但是，此结果，并不能证明1+1=2，只能证明另两个自然数相加，满足前4条公理的情况下，等式才成立。

不知道各位怎么看待这个问题，欢迎大家留言讨论。