r语言 随机森林_用R语言模拟M / M / 1随机服务排队系统

原文链接：

http://tecdat.cn/?p=8199​tecdat.cn

本文中我在R中构造一个简单的M / M / 1队列的离散事件模拟 。

模拟变量
像往常一样，我们从模拟及其检测所需的变量 开始。

2. 
   t.end <- 10^5 # duration of sim
3. 
   t.clock <- 0 # sim time
4. 
   Ta <- 1.3333 # interarrival period
5. 
   Ts <- 1.0000 # service period
6. 
   t1 <- 0 # time for next arrival
7. 
   t2 <- t.end # time for next departure
8. 
   tn <- t.clock # tmp var for last event time
9. 
   tb <- 0 # tmp var for last busy-time start
10. 
    n <- 0 # number in system
11. 
    s <- 0 # cumulative number-time product
12. 
    b <- 0 # total busy time
13. 
    c <- 0 # total completions
14. 
    qc <- 0 # plot instantaneous q size
15. 
    tc <- 0 # plot time delta
16. 
    plotSamples <- 100
17. 
    set.seed(1)

接下来，我们需要编写R代码以对进入队列和从队列离开进行实际的M / M / 1模拟。

仿真循环

1. 
   while (t.clock < t.end) {
2. 
   if (t1 < t2) { # arrival event
3. 
   t.clock <- t1
4. 
   s <- s + n * (t.clock - tn) # delta time-weighted number in queue
6. 
   ...
8. 
   else {
9. 
   t2 <- t.end
10. 
    b <- b + t.clock - tb
11. 
    }
12. 
    }
13. 
    }

检测指标
在这里，我们 检测数据以形成一些众所周知的性能指标。

队列长度
这是瞬时队列长度- 平均负载数据的曲线图。这就是排队波动的样子。

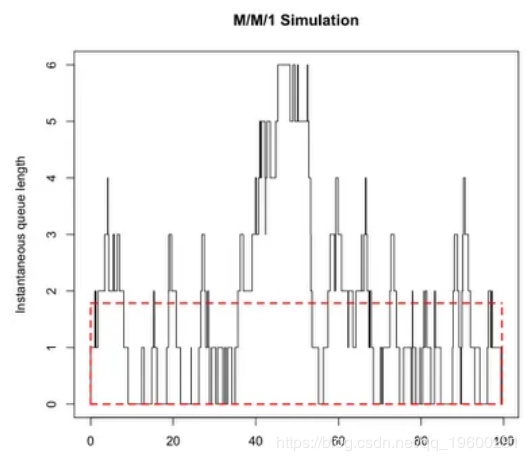
显示为红色虚线的框具有与阶梯曲线下方相同的面积。

PDQ模型
为了进行分析比较，我们还使用 PDQ-R模型。

是的，这几行代码与上面带工具的仿真代码等效，并且可以保证处于稳定状态。即使在R中运行PDQ本质上也是瞬时的。模拟将花费更长的时间，

结果
最后，我们可以将模拟的M / M / 1队列与相应的PDQ结果进行比较。像往常一样，最好将它们分解为输入和输出。

1. 输入：
   1. 
      Tsim：1.00e + 05
   2. 
      Ta：1.3333，Ts：1.0000＃次
   3. 
      Ar：0.7500，Sr：1.0000＃

1. 输出：
   1. 
      Usim：0.7477，Updq：0.75
   2. 
      Xsim：0.7495，Xpdq：0.75
   3. 
      Rsim：4.0316，Rpdq：4.00
   4. 
      Qsim：3.0219，Qpdq：3.00

我们可以得出结论，仿真在指定的10 5个时间步长内达到了稳态。