正态分布某一点的概率怎么算_概率分布知识总结

随机变量

随机变量分为离散型随机变量与连续型随机变量

离散型随机变量的概率计算公式为概率质量函数（PMF），统计图中的形状为离散概率分布

连续型随机变量的概率计算公式为概率密度函数（PDF），统计图中的形状为连续概率分布

离散概率分布

离散随机变量（概率质量函数PMF），其中常见的包括伯努利分布、二项分布、几何分布和泊松分布

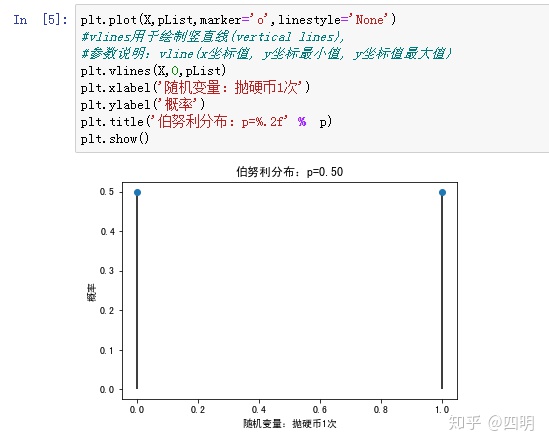
一、伯努利分布（0-1分布）

单次随机试验，只有"成功（值为1）"或"失败（值为0）"这两种结果，记成功概率为p(0≤p≤1)，则失败概率为q=1-p。

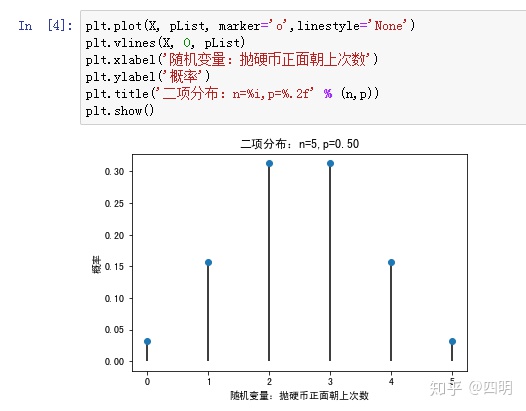
二、二项分布

二项分布即重复N次独立的伯努利分布，二项分布求出的结果即某事件发生x次的概率

p表示成功的概率；k表示想知道成功的次数。P（X=k)=C(n,k)（p^k）*(1-p)^(n-k)。

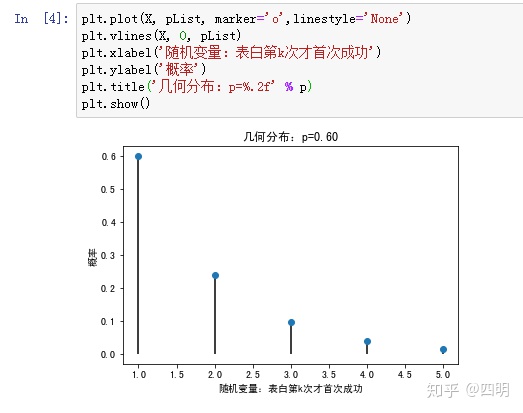
三、几何分布

几何分布同样以伯努利分布为基础，即在N次伯努利分布试验中，试验k次才第一次获得成功的概率

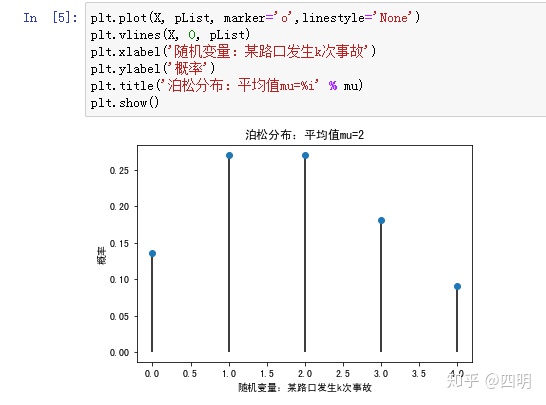
四、泊松分布

一个事件在一段时间内随机发生，其服从泊松分布的条件为：

（1）将该时间段无限分隔成很多个小的时间段，在这个小的时间段内，事件发生的概率非常小，不发生的概率非常大。

（2）在每个小的时间段内，事件发生的概率是稳定的，且与小的时间段的长度成正比。

（3）该事件在不同的小时间段里，发生与否相互独立。

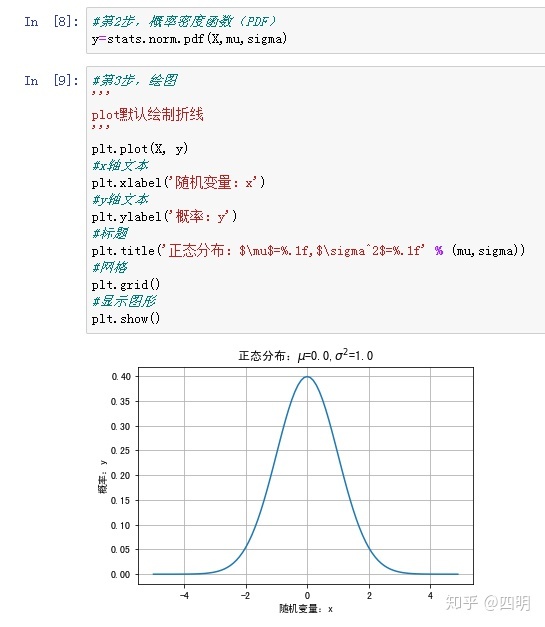
二、正态分布

正态分布属于连续型随机变量，若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

因为是连续性随机变量，求概率函数为概率密度函数（PDF）

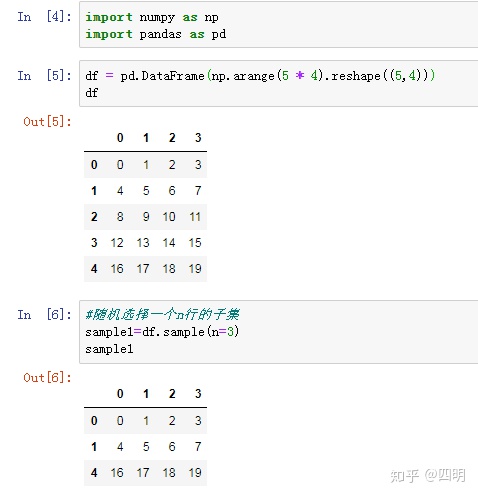
三、总体和样本

导入随机数random模块，抽奖案例以及数据框抽样方法

四、中心极限定理

1、样本的平均值约等于总体平均值；不管总体是什么分布，任意总体的样本平均值都会围绕在总体的平均值周围，并且呈正态分布。

2、用样本估计总体标准差

公式总结：

1. 伯努利分布：stats.bernoulli.pmf(随机变量X，单次概率p)
2. 二项分布：stats.binom.pmf(随机变量X，做事情的次数n，单次概率p)
3. 几何分布：stats.geom.pmf(随机变量X，单次概率p)
4. 泊松分布：stats.poisson.pmf(随机变量X，平均发生次数mu)
5. 正态分布：stats.norm.pdf(随机变量X，平均值mu，标准差sigma)