实数系的基本定理_一个看似极其显然，证明却极其困难的数学定理

网上曾经流行过一个关于数学的段子：

这个段子真真切切地道出了数学系学生的日常，的确，专业数学里面到处充斥着看起来非常显然，但是又需要用复杂的数学工具才能证明的命题，今天我们就来看一个非常典型的例子。

高中时我们都学过所谓的零点定理或叫介值定理，它叙述起来是这个风格的：

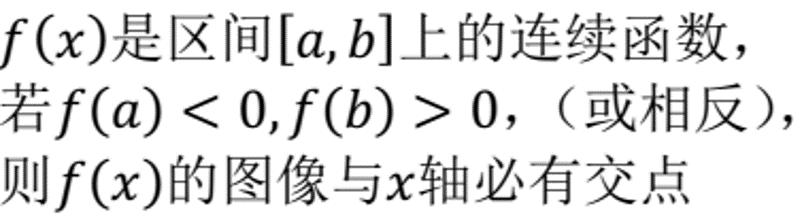
它画出图来是这个风格的：

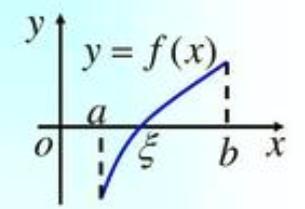
这个定理是如此的简单、直白且明显，以至于当我说它也需要证明时，很多人也会像上图中的哈利波特一样惊呼：天呐，我们为什么还要证它，以及我们该如何证它？

事实上，数学就是一个环环相扣，逻辑严密的推导体系，任何一个定理的产生都不是空穴来风，都需要有先前的定理或公理作为保证。即使是它看起来如此的显然，我们也不能天然地认为它就是正确的。

零点定理的证明从理论上来讲有6种，我选择其中一种写法最简洁的来介绍，即使如此，要完整的叙述也要写好长一段，并且需要一些预备的概念和预备的定理。

预备概念：上确界

若一个数集中所有的数都小于等于某一个实数，那么这个数集称为有上界的，这个实数称为数集的一个上界。

显然一个有上界的数集，它的上界不止一个，例如开区间(0，1)，1、2、3、4、5...，都是它的上界。但在这么多的上界中，有一个最小的就是1，那么就把1称之为它的上确界。

定义：一个有上界的数集，它的所有上界中最小的那一个，称为该数集的上确界。

预备定理：实数集的任何一个有上界的非空子集都有一个实数作为它的上确界。

这个定理看起来毫不起眼，但事实上，实数在这里起着决定性的作用。如果换成其它的数比如有理数：有理数集的任何一个有上界的非空子集，都有一个有理数作为它的上确界，这句话就是错误的。比如考虑这样一个由有理数组成的集合：

｛1，1.4，1.41，1.414，1.4142...｝，这个集合的上确界是根号2，但根号2并不是有理数。

事实上，上述定理被称为确界原理，确界原理是实数集合的一个本质刻化，整个微积分的大厦，就是建立在实数集的这种特征之上的。

好了，有了上述准备工作，就可以进行零点定理的证明了。

至此证明完毕，相信肯定会有很多小伙伴再一次被数学的这种严谨性所震撼。当然，本证明过程中所使用的确界原理也是需要证明的，而它的证明则又需要利用实数的定义，例如康托尔(Cantor，德国数学家)曾将提出了用有理数基本序列来定义实数，以及更广泛被人们所采用的戴德金(Dedekind，德国数学家)分割来定义实数，这又是另外一番故事了。其实本文标题中说证明极其困难，主要指的是确界原理的证明及其困难，要想完整证明它，文章将长度将数倍于本文。

这个定理还有更高形式的推广——若尔当曲线定理，这个定理简单地说就是，平面上有一个闭合的圈，在圈内取一点，在圈外取一点，那么连接这两个点的任意一条连续曲线一定和圈有交点。

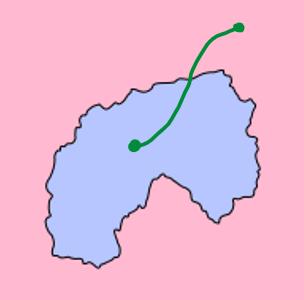
若尔当曲线定理的一个简单图解

这个定理看起来同样是简单得令人可笑，但是其证明过程却极其复杂，它的困难之处在于如何描述一个“闭合的圈”，这需要使用到代数拓扑学的知识，那将是以后的话题了。