Mathematics->Fourier series(real number field)
非完备性证明,逻辑自洽,深入浅出,构建光通信数学观。
光通信与数学 - 基础1
光通信与数学 - 泰勒展开式与欧拉公式
 创造一个属于你自己的变换
微积分
创造一个属于你自己的变换
微积分
透支一部分微积分基础知识,但不会涉及梯度,偏微分等复杂概念。
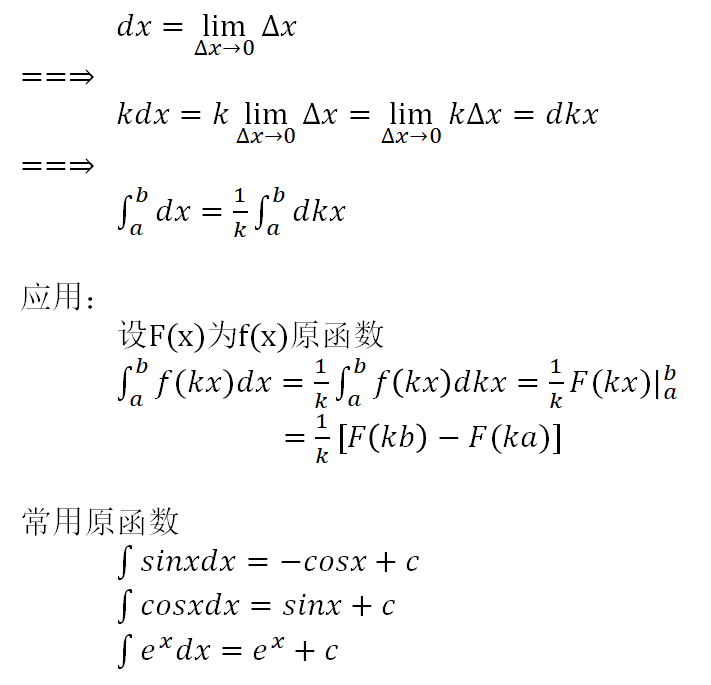
三角函数补充
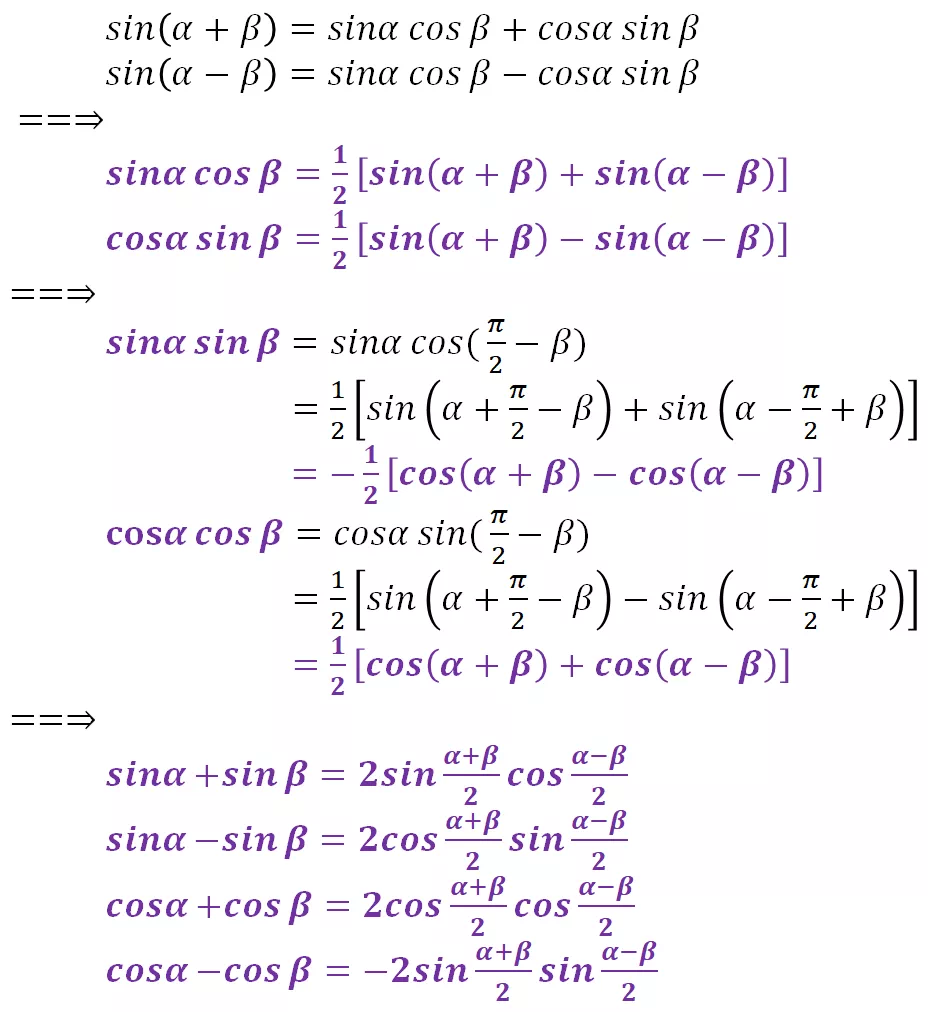
内积补充
内积即两个元素点乘,是元素之间的投影计算,若内积为0,表示两个元素正交,即两个元素之间无关系。
向量内积
基础1篇说明了向量内积概念,并给出了几何定义推导。
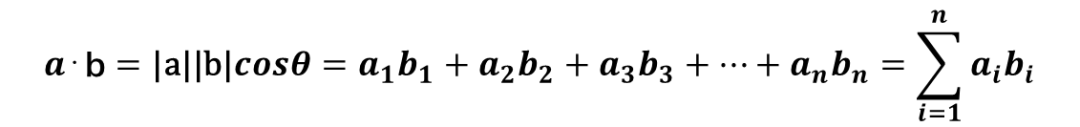
关于代数定义推导以及如何从代数定义推导出几何定义,如下:

将向量从2维空间扩展到多维空间即对应完整定义。
函数内积(实数域)
内积可以从向量扩充到函数。
实数域内,函数内积定义:
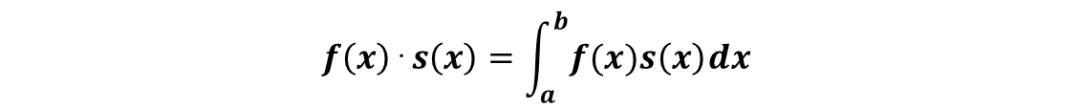
向量由离散的点表示:
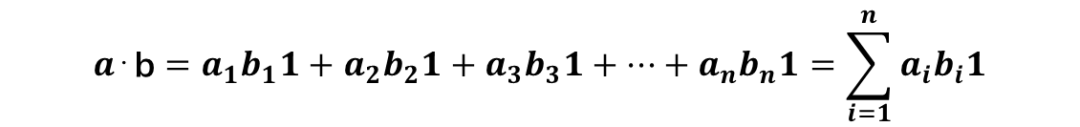
每项乘积的系数1理解为离散点的计数或权重。
函数由连续不可计数的点表示,函数内积:
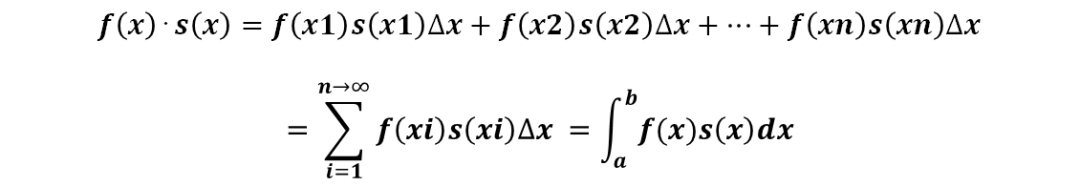
每项乘积的系数Δx理解为不可计数点的计数或权重。
正交基&变换
正交基由一组元素两两内积为0(即两两正交)组成,构建一个内积空间。
如果基内所有元素同自己内积都为1,则该正交基为标准正交基。
如果在内积空间内找不到另外一个元素与正交基内所有元素都两两正交,则该正交基为对应内积空间的完备正交基。
2维空间变换
构建一个2维直角坐标系,任何一个坐标轴上向量称为该轴的基,(1, 0)为x轴的基,(0, 1)为y轴的基。(1, 0)和(0, 1)是对应2维空间的完备标准正交基。
对于空间中的任意一个向量s,构建的2维平面空间与s共面,通过内积计算s在该2维坐标系中的坐标表达s(sx, sy)。
将s和x轴上标准基做内积,s⋅(1, 0)等于x轴上的投影值a,得到sx = a
将s和y轴上标准基做内积,s⋅(0, 1)等于y轴上的投影值b,得到sy = b
s(sx, sy) = sx⋅(1, 0)+sy⋅(0, 1) = s(a, b),即向量V可以用2维空间的正交基变换而来,坐标值sx、sy为变换系数。
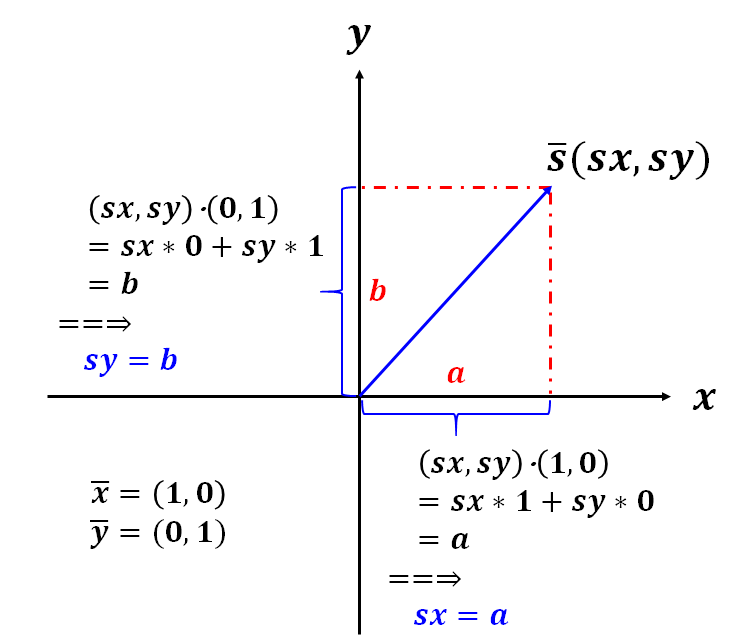
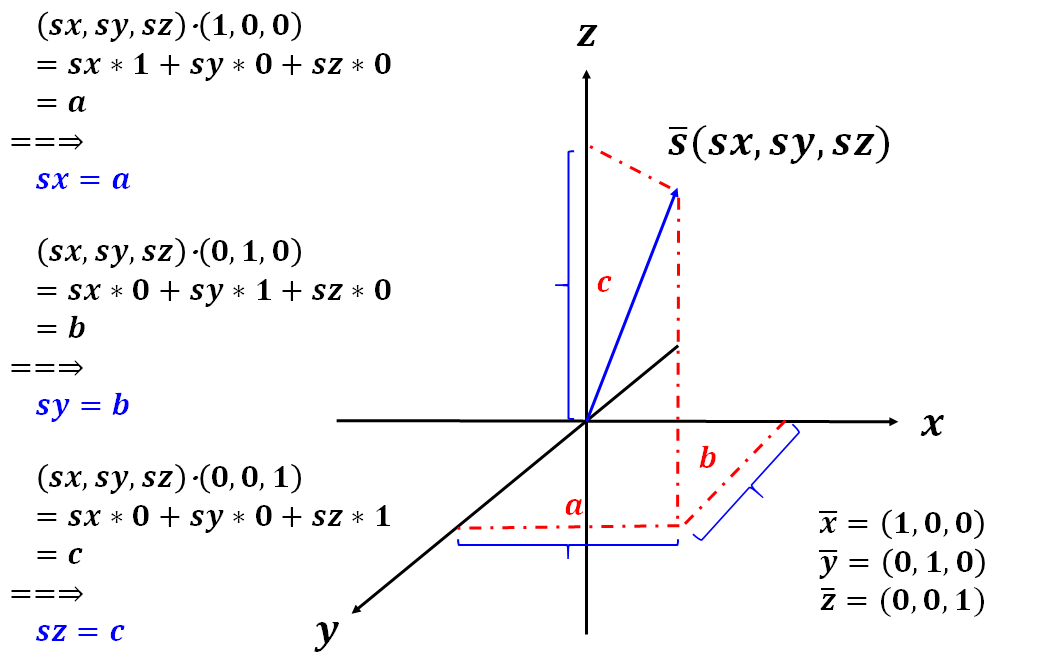
3维空间变换
向量(1, 0, 0),(0, 1, 0),(0, 0, 1)构成3维直角坐标轴,是对应3维空间的完备标准正交基。
同样的空间向量s变换到3维坐标系中,通过内积计算s在该3维坐标系中坐标表达s(sx, sy, sz)。
将s和x轴上标准基做内积,s⋅(1, 0, 0)等于x轴上的投影值a,得到sx = a
将s和y轴上标准基做内积,s⋅(0, 1, 0)等于y轴上的投影值b,得到sy = b
将s和z轴上标准基做内积,s⋅(0, 0, 1)等于z轴上的投影值c,得到sz = c
s(sx, sy, sz) = sx⋅(1, 0, 0)+sy⋅(0, 1, 0)+sz⋅(0, 0, 1)= s(a, b, c),即向量s可以用3维空间的正交基变换而来,坐标值sx、sy、sz为变换系数。
n维空间变换
空间向量s可以变换到2维空间和3维空间,类推也可以变换到n维空间,变换方式推导:

在变换过程中,正交基需要是完备的,但不需要是标准的,因为可以通过调节变换系数来平衡。
正余弦空间
向量可以组成向量内积空间,函数是否能组成函数内积空间呢,三角函数系{1, sinnx, cosnx | n=1,2,3,...} 是一组在[-π,π]区间上的完备正交基,该正交基构成了正余弦空间,对其完备性暂不做证明。
用元素两两内积是否为0来证明正交性:

上述证明过程可知,三角函数系是[-π,π]区间内正交基,但不是标准正交基。
分析:
sinkx的周期为P=2π/k。
{sinnx, cosnx | n=1,2,3,...}内所有函数最大的周期为2π,与区间[-π,π]大小一致。
区间是[-π,π],也可以是[0,2π],只要是[a, b]满足b-a=2π均可。
扩展:
{sinnkx, cosnkx | n=1,2,3,...}内所有函数最大的周期为2π/k,推断三角函数系{1, sinnkx, cosnkx | n=1,2,3,...} 是一组在[-π/k, π/k]区间内的完备正交基,证明类似上述过程。
问题:
Q:n一定要是整数吗,能不能取小数?
A:取小数时函数与正交基内其它函数两两内积不等于0,不满足正交性。
Q:n能不能等于0,为什么正交基会有一个1?
A:如果n=0,则sin0=0,cos0=1。sin0与其他正余弦函数内积等于0,sin0自我内积也等于0,是一个没意义的基。cos0与其他正余弦函数内积等于0,cos0自我内积等于2π,是一个有意义的基。因此n不取0,但是保留cos0=1做为正交基的组成。
Q:n能不能是负数?
A:对于cosnx,cos(-nx)=cosnx,实际都是同一个基,取负数无意义。对于sinnx,sin(-nx)⋅sinnx=-sinnx⋅sinnx=-π,不满足正交性。因此n不取负数。
Q:空间向量能变换到n维空间内,函数变换到正余弦空间会发生什么?
A:后续做推导来揭晓答案。
Q:周期P无限大会发生什么?
A:后续做推导来揭晓答案。
傅里叶级数推导(实数域)
正余弦空间变换
空间向量s可以变换到n维空间,函数s(x)在区间[-π,π]内是否可以变换到正余弦空间呢,正余弦空间的正交基为{1, sinnx, cosnx | n=1,2,3,...} ,假设该变换存在,则表达式为每个维度的基乘以变换系数再求和:
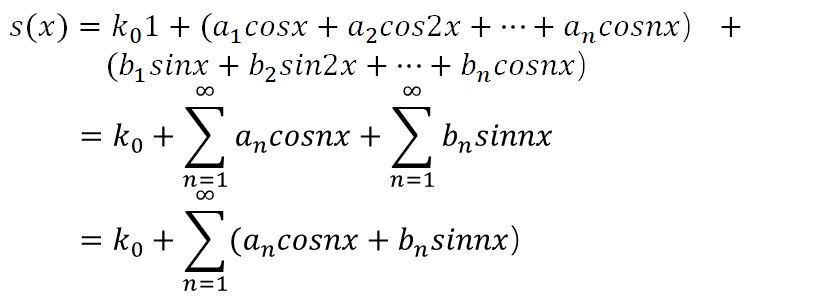
将s(x)与每个基内积,计算对应基的变换系数:

从上述推导过程可知,如果s(x)在区间内绝对可积,则变换系数就存在,即s(x)能在区间[-π,π]内变换到正余弦空间。
如果s(x)是以2π为周期的函数,即s(x+2kπ)=s(x),那么s(x)在[-∞, ∞]上都能变换到正余弦空间,变换表达式如下:
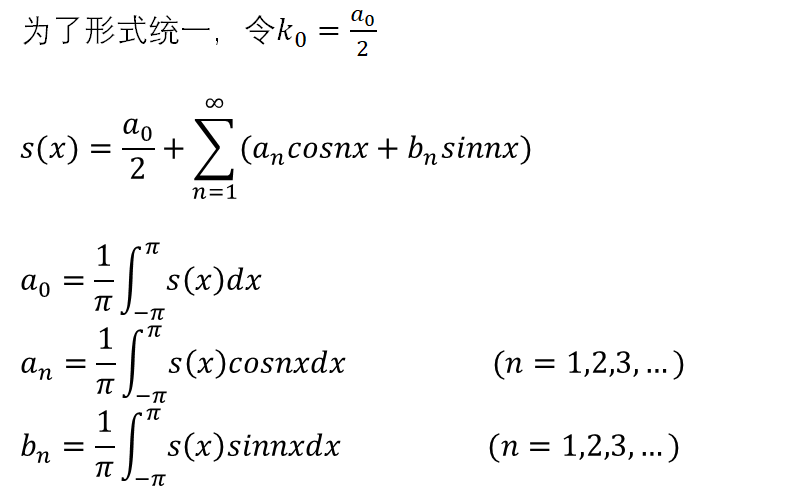
如果s(x)是以P为周期的函数,即s(x+P)=s(x),需要调整正余弦空间正交基以适配周期P。

将周期函数s(x)在正余弦空间的变换表达式展开是一个无穷级数,被称为傅里叶级数,类似于泰勒级数(泰勒展开式),是对于原函数s(x)的一种近似表达,当级数无穷大时,认为无限逼近于原函数。
函数空间变换
上述变换推导是专门针对正余弦函数空间进行的,对于一般性的函数空间是否存在通用性的函数泛型变换算法呢,做以下推导。

用函数泛型变换算法来重新推导验证傅里叶级数。

推导可知,函数泛型变换算法结果与前面特定推导保持一致!
傅里叶级数意义(实数域)
正余弦变换几何意义
通过三角函数变换,可以将相位为0的正余弦合并成初始相位不为0的正弦。
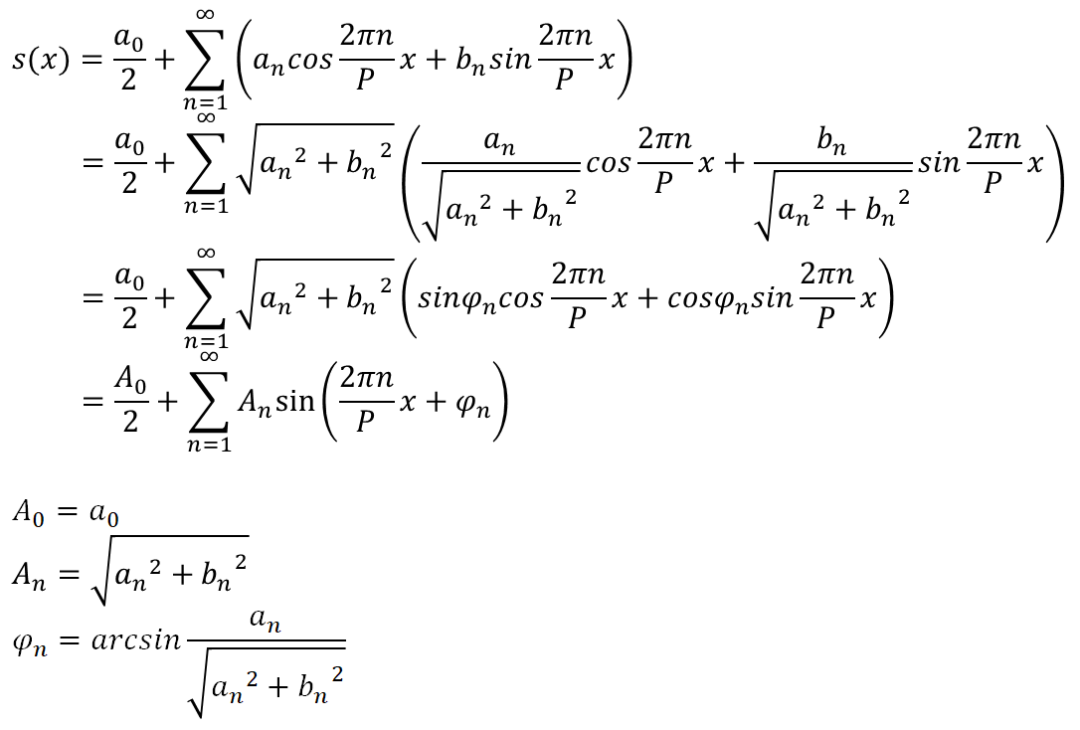
综合归纳,周期函数s(x)可以变换为一系列的初始0相位的正余弦波组成,也可以为一系列的带初始相位的正弦波组成。
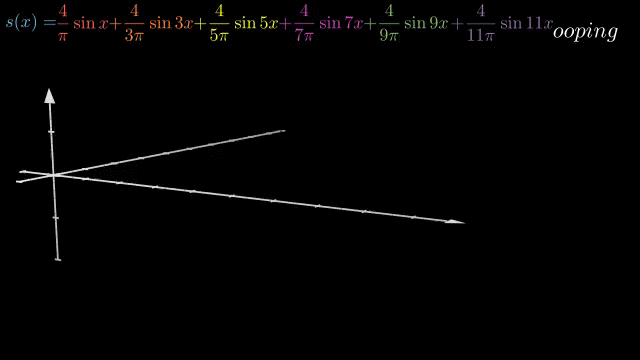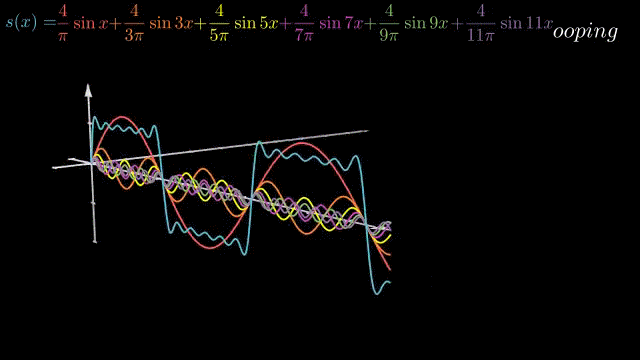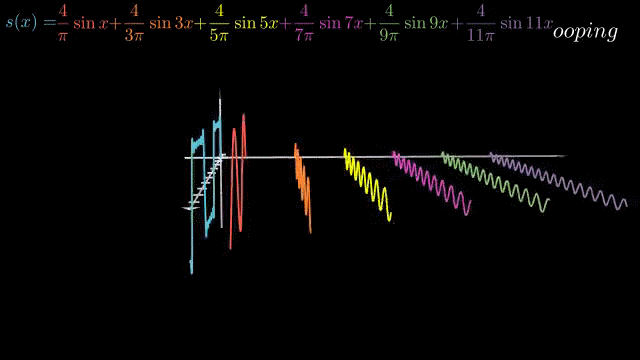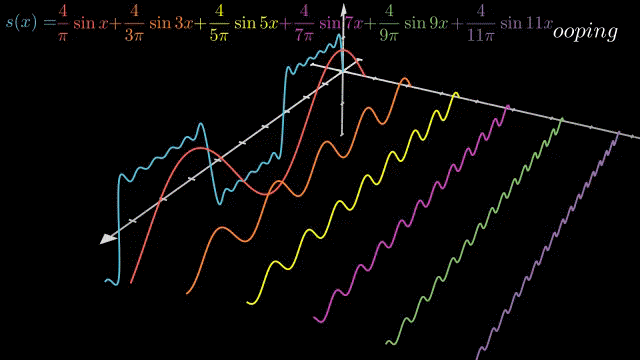
矩形波的傅里叶级数
周期为2π的方波,计算其傅里叶级数。

进行python数学模拟,随着结果级数的增多,合成图形越来越接近周期方波,如果级数无穷大,则无限逼近方波。

奇葩问题
周期为2π的方波,也可以理解为周期为4π或6π的周期波,是否会影响傅里叶级数变换呢,以4π为例进行说明:

推导显示结果一致,但计算过程变复杂,所以变换系数的计算需采取最小的周期。
时域变换到频域
对于函数或信号s(x),如果自变量x代表时间t(以秒为单位),则称s(x)为时域函数或信号。
如果s(x)的傅里叶级数存在,则s(x)可以展开为一系列的正余弦函数,每个正余弦函数都有振幅A和频率ε,如sinkx的频率ε=k(以赫兹为单位)。
以方波函数为例,增加一个频率轴,将不同频率的正余弦波分开,可从频域的角度观察s(x)。
角频率形态

光通信与数学剩余内容
傅里叶级数(复指数域)
傅里叶变换
离散傅里叶变换与卷积
微积分
OOPING
18171226206 (WeChat)
ooping@amazelink.cn
每周不超过50%的几率随机更新,专注光通信与数学、物理、软件的交集!
 创造一个属于你自己的变换
微积分
透支一部分微积分基础知识,但不会涉及梯度,偏微分等复杂概念。
创造一个属于你自己的变换
微积分
透支一部分微积分基础知识,但不会涉及梯度,偏微分等复杂概念。
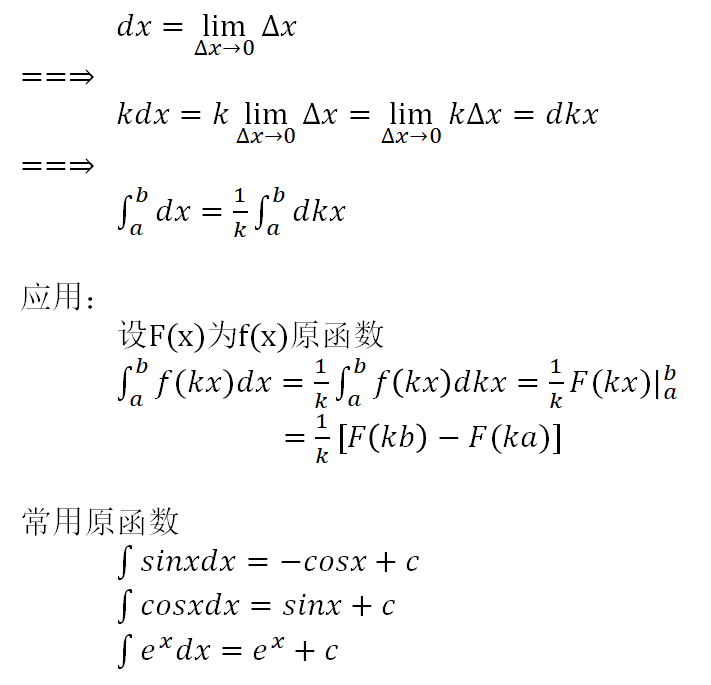
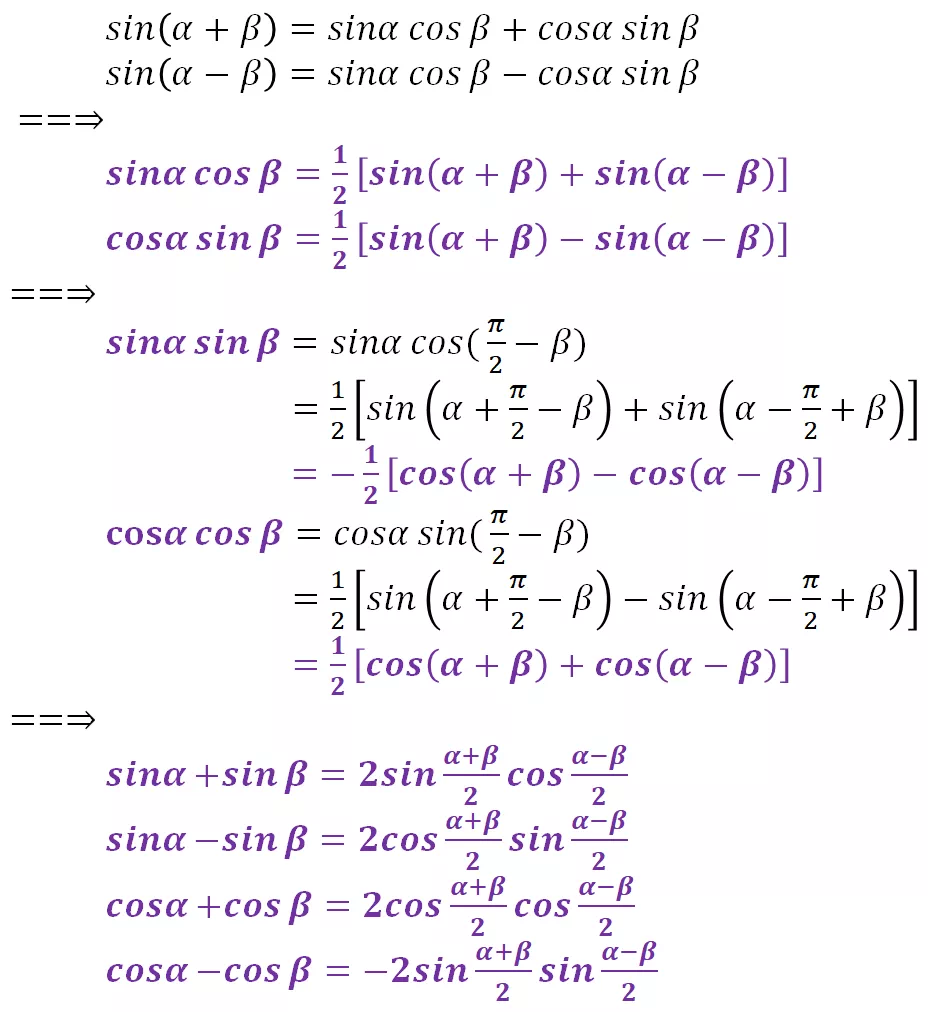
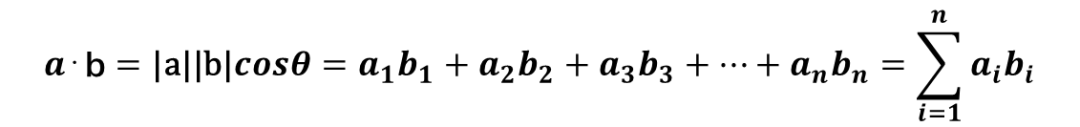

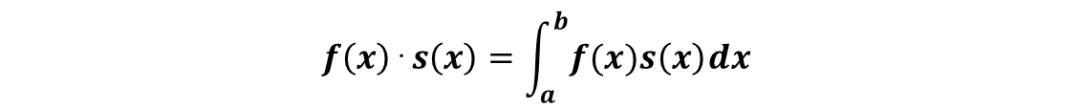
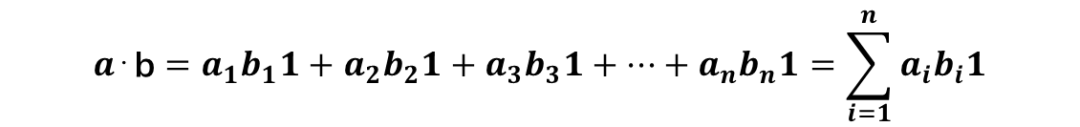
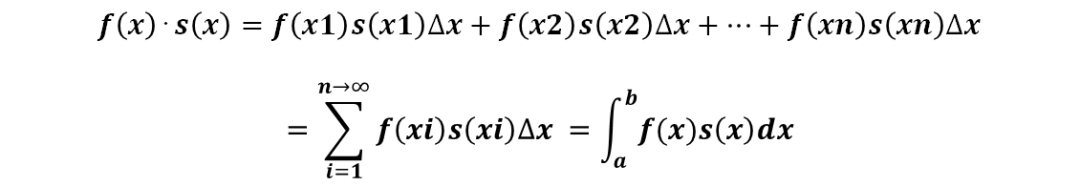
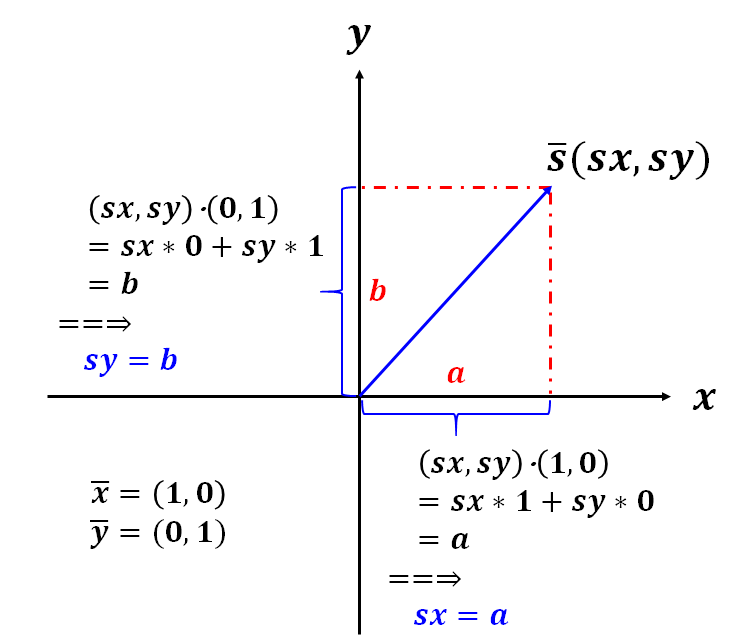



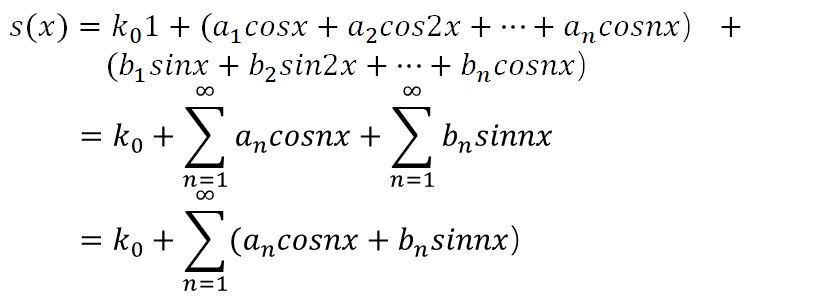

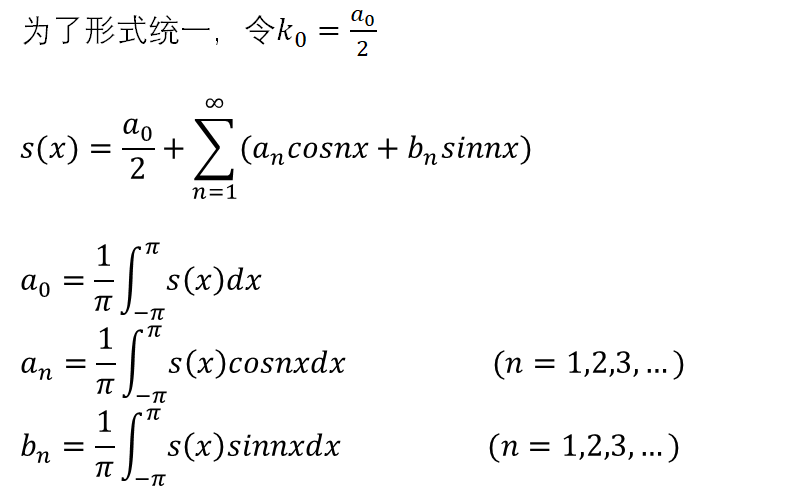



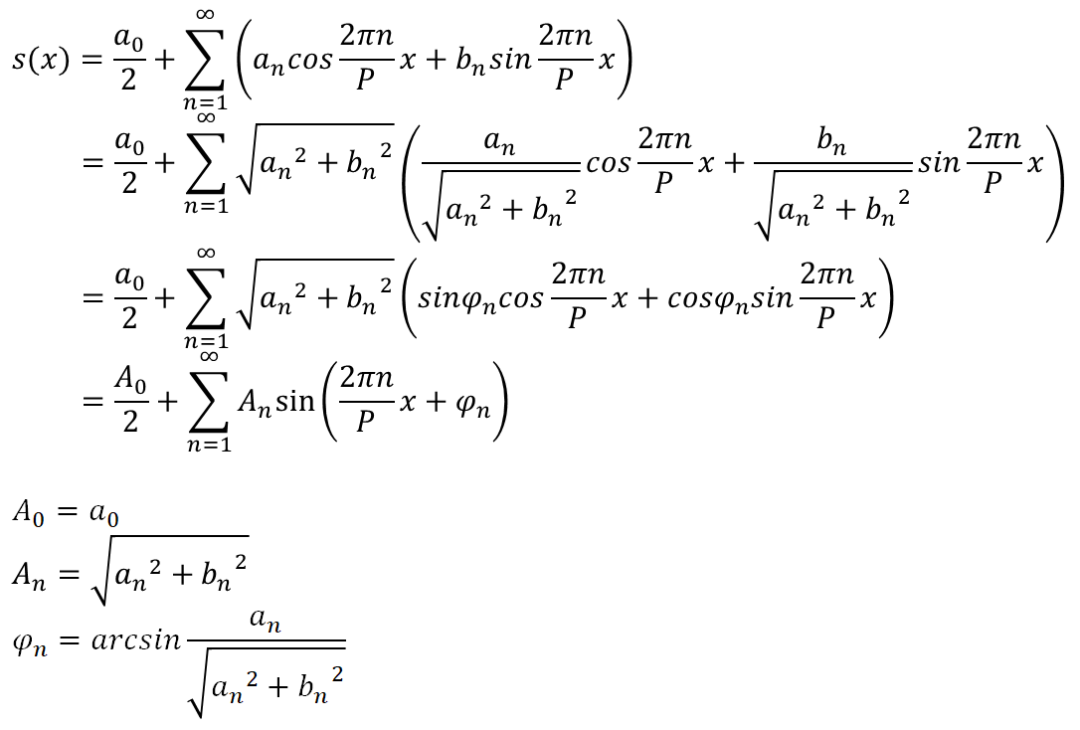

 奇葩问题
周期为2π的方波,也可以理解为周期为4π或6π的周期波,是否会影响傅里叶级数变换呢,以4π为例进行说明:
奇葩问题
周期为2π的方波,也可以理解为周期为4π或6π的周期波,是否会影响傅里叶级数变换呢,以4π为例进行说明:























 1745
1745











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








