 关注↑↑↑获得更多精彩内容!
关注↑↑↑获得更多精彩内容!
教育意味着获得不同的视角,理解不同的人、经历和历史。
接受教育,但不要让你的教育僵化成傲慢。
教育应该是思想的拓展,同理心的深化,视野的开阔。
它不应该使你的偏见变得更顽固。
如果人们受过教育,他们应该变得不那么确定,而不是更确定。
他们应该多听,少说,对差异满怀激情,热爱那些不同于他们的想法。
——塔拉·韦斯特弗

一、知识要点
(一)圆柱、圆锥、圆台的侧面积 将侧面沿母线展开在平面上,则其侧面展开图的面积即为侧面面积。 1、圆柱的侧面展开图——矩形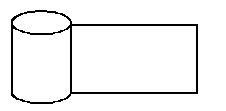 圆柱的侧面积
圆柱的侧面积
 2、圆锥的侧面展开图——扇形
2、圆锥的侧面展开图——扇形
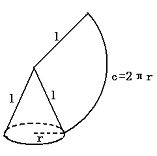 圆锥的侧面积
圆锥的侧面积
 3、圆台的侧面展开图——扇环
3、圆台的侧面展开图——扇环
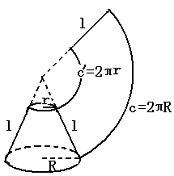 圆台的侧面积
圆台的侧面积
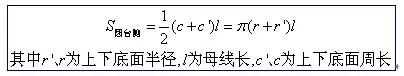 (二)直棱柱、正棱锥、正棱台的侧面积
把侧面沿一条侧棱展开在一个平面上,则侧面展开图的面积就是侧面的面积。
1、柱的侧面展开图——矩形
(二)直棱柱、正棱锥、正棱台的侧面积
把侧面沿一条侧棱展开在一个平面上,则侧面展开图的面积就是侧面的面积。
1、柱的侧面展开图——矩形
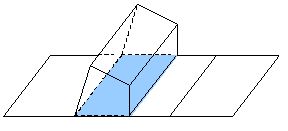 直棱柱的侧面积
直棱柱的侧面积
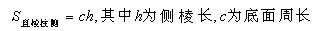 2、锥的侧面展开图——多个共点三角形
2、锥的侧面展开图——多个共点三角形
 正棱锥的侧面积
正棱锥的侧面积
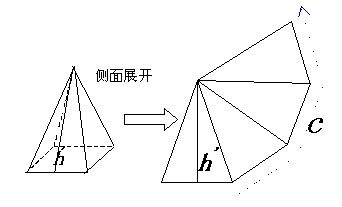
 3、正棱台的侧面展开图——多个等腰梯形
3、正棱台的侧面展开图——多个等腰梯形
 正棱台的侧面积
正棱台的侧面积
 说明:这个公式实际上是柱体、锥体和台体的侧面积公式的统一形式
①即锥体的侧面积公式;
②c'=c时即柱体的侧面积公式;
(三)棱柱和圆柱的体积
说明:这个公式实际上是柱体、锥体和台体的侧面积公式的统一形式
①即锥体的侧面积公式;
②c'=c时即柱体的侧面积公式;
(三)棱柱和圆柱的体积
 斜棱柱的体积=直截面的面积×侧棱长
(四)棱锥和圆锥的体积
斜棱柱的体积=直截面的面积×侧棱长
(四)棱锥和圆锥的体积
 (五)棱台和圆台的体积
(五)棱台和圆台的体积
 说明:这个公式实际上是柱、锥、台体的体积公式的统一形式:
①
说明:这个公式实际上是柱、锥、台体的体积公式的统一形式:
①
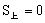 时即为锥体的体积公式;
②S上=S下时即为柱体的体积公式。
(六)球的表面积和体积公式
时即为锥体的体积公式;
②S上=S下时即为柱体的体积公式。
(六)球的表面积和体积公式
 (七)简单的组合几何体的表面积和体积——割补法的应用
割——把不规则的组合几何体分割为若干个规则的几何体;
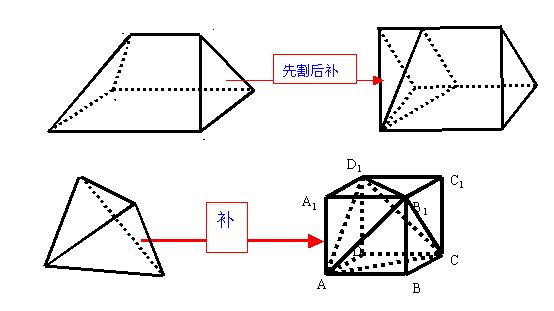
补——把不规则的几何体通过添补一个或若干个几何体构造出一个规则的新几何体,如正四面体可以补成一个正方体,如图:
(七)简单的组合几何体的表面积和体积——割补法的应用
割——把不规则的组合几何体分割为若干个规则的几何体;
补——把不规则的几何体通过添补一个或若干个几何体构造出一个规则的新几何体,如正四面体可以补成一个正方体,如图:
二、考点与典型例题
考点一 几何体的侧面展开图 【例1】有一根长为5cm,底面半径为1cm的圆柱形铁管,用一段铁丝在铁管上缠绕4圈,并使铁丝的两个端点落在圆柱的同一母线的两端A、D,则铁丝的最短长度为多少厘米?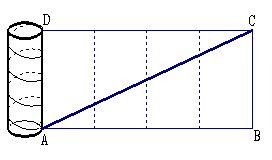 解:展开后使其成一线段AC=
解:展开后使其成一线段AC=
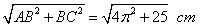 考点二 求几何体的面积
【例2】设计一个正四棱锥形的冷水塔顶,高是0.85m,底面的边长是1.5m,制造这种塔顶需要多少平方米铁板?(保留两位有效数字)
考点二 求几何体的面积
【例2】设计一个正四棱锥形的冷水塔顶,高是0.85m,底面的边长是1.5m,制造这种塔顶需要多少平方米铁板?(保留两位有效数字)
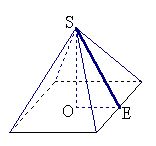 解:
解:
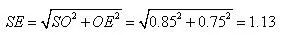
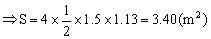 答:略。
考点三 求几何体的体积
【例3】求棱长为
答:略。
考点三 求几何体的体积
【例3】求棱长为
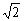 的正四面体的体积。
的正四面体的体积。
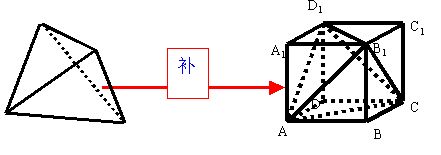 分析:将正四面体通过补形使其成为正方体,然后将正方体的体积减去四个易求体积的小三棱锥的体积。
解:如图,将正四面体补形成一个正方体,则正方体的棱长为1,则:V正四面体=V正方体-4V三棱锥=1-
分析:将正四面体通过补形使其成为正方体,然后将正方体的体积减去四个易求体积的小三棱锥的体积。
解:如图,将正四面体补形成一个正方体,则正方体的棱长为1,则:V正四面体=V正方体-4V三棱锥=1-
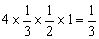 。
考点四 求不规则几何体的体积
【例4】证明四面体的体积
。
考点四 求不规则几何体的体积
【例4】证明四面体的体积
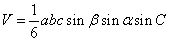 ,其中a,b,c为自同一顶点S出发的三条棱SA、SB、SC的长,α,β为点S处的两个面角∠BSC、∠ASC,C为这两个面所夹二面角的大小。
,其中a,b,c为自同一顶点S出发的三条棱SA、SB、SC的长,α,β为点S处的两个面角∠BSC、∠ASC,C为这两个面所夹二面角的大小。
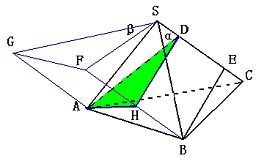 证明:通过补形,可将此三棱锥补成一个三棱柱,如图。则该三棱柱的体积可以利用“直截面面积×侧棱长”来进行求解,若设过A点的直截面为AHD,则由题意知:∠ADH=C;
又AD⊥SC,故AD=SA×sinβ=a·sinβ;
若过B作BE⊥SC于E,则BE=HD=BC×sinα=b·sinα.所以,
证明:通过补形,可将此三棱锥补成一个三棱柱,如图。则该三棱柱的体积可以利用“直截面面积×侧棱长”来进行求解,若设过A点的直截面为AHD,则由题意知:∠ADH=C;
又AD⊥SC,故AD=SA×sinβ=a·sinβ;
若过B作BE⊥SC于E,则BE=HD=BC×sinα=b·sinα.所以,
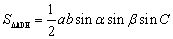 从而有
从而有
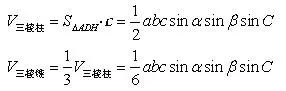 。
考点五 球的表面积和体积
【例5】 在球心的同侧有相距为9的两个平行截面,它们的面积分别为49π和400π,求球的表面积和体积。
分析:画出球的轴截面,利用球的截面性质求球的半径
解:设球的半径为R,O为球心,O1、O2分别是截面圆的圆心,如图。
。
考点五 球的表面积和体积
【例5】 在球心的同侧有相距为9的两个平行截面,它们的面积分别为49π和400π,求球的表面积和体积。
分析:画出球的轴截面,利用球的截面性质求球的半径
解:设球的半径为R,O为球心,O1、O2分别是截面圆的圆心,如图。
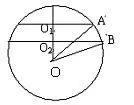 则O1A=7,O2B=20,OA=OB=R,从而分别解三角形OO2B和三角形OO1A得到OO1和OO2,由OO1-OO2=9解得R=25,从而
球的表面积为2500π,球的体积为
则O1A=7,O2B=20,OA=OB=R,从而分别解三角形OO2B和三角形OO1A得到OO1和OO2,由OO1-OO2=9解得R=25,从而
球的表面积为2500π,球的体积为
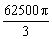 。
考点六 求点到平面的距离——等积法的应用
【例6】在正方体ABCD-A’B’C’D’中,已知棱长为a,求B到平面AB’C的距离。
。
考点六 求点到平面的距离——等积法的应用
【例6】在正方体ABCD-A’B’C’D’中,已知棱长为a,求B到平面AB’C的距离。
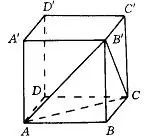 解:设B到面AB’C的距离为h,因为AB’=B’C=CA=
解:设B到面AB’C的距离为h,因为AB’=B’C=CA=
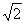 a,
所以SΔAB’C=
a,
所以SΔAB’C=
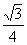 (
(
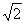 a)
a)
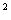 =
=
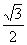 a
a
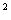 ,
因此
,
因此
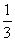 ·
·
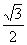 a
a
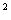 ·h=VB-AB′C= VB′-ABC =
·h=VB-AB′C= VB′-ABC =
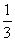 ·
·
 a
a
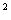 ·a=
·a=
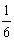 a
a
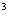 ,
故h=
,
故h=
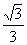 a,即B到面AB′C的距离为
a,即B到面AB′C的距离为
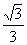 a。
考点七 拟柱体通用体积公式
拟柱体:所有的顶点都在两个平行平面内的多面体叫做拟柱体.它在这两个平面内的面叫做拟柱体的底面.其余各面叫做拟柱体的侧面,两底面之间的距离叫做拟柱体的高。
a。
考点七 拟柱体通用体积公式
拟柱体:所有的顶点都在两个平行平面内的多面体叫做拟柱体.它在这两个平面内的面叫做拟柱体的底面.其余各面叫做拟柱体的侧面,两底面之间的距离叫做拟柱体的高。
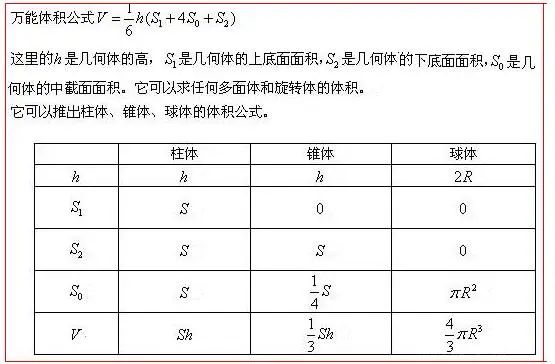
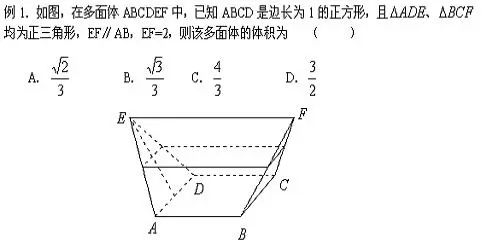
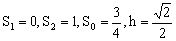
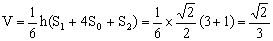 ,选A。
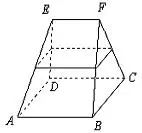
【例2】 如图所示,在多面体ABCDEF中,已知ABCD是边长为3的正方形,EF//AB,
,选A。
【例2】 如图所示,在多面体ABCDEF中,已知ABCD是边长为3的正方形,EF//AB,
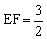 ,EF与面AC的距离为2,则该多面体的体积为( )
A.
,EF与面AC的距离为2,则该多面体的体积为( )
A.
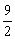 B. 5
C. 6
D.
B. 5
C. 6
D.
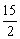

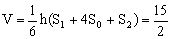 ,选D。
,选D。
三、涉及的主要数学思想方法
计算能力是中学生要掌握的最基本的能力之一。 立体几何的题型从内容上可分为两大类,一是空间位置关系的研究,二是空间量度(主要是角度与距离)的求解,也是高考命题中立体几何的两类基本题型。 本讲主要考查空间图形的面积与体积的计算能力,对空间想象能力的要求也比较高,因为在运用公式求解之前,必须先求相关的角度与距离。 要通过对几种特殊几何体的面积和体积公式的推导,掌握割补法、等积变换法等重要数学方法在解决面积与体积求解问题中的应用。 所以,对空间图形的变换能力的要求较高,要通过一些典型的空间图形变换的例子,掌握变换技巧,从而化难为易,化不规则为规则,达到快速求解的目的。 — END — 本文来源于
数学好老师
。版权归原作者所有,若侵删。
本文来源于
数学好老师
。版权归原作者所有,若侵删。
小知识分享
数学中,新课改提出的“三会”:会用数学的眼光观察世界、会用数学的思维思考世界、会用数学的语言表达世界。
四有好老师:“有理想信念,有道德情操,有扎实学识,有仁爱之心”。
数学学科核心素养:数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析。
“四基”:数学基础知识、数学基本技能、数学基本思想、数学基本活动经验。
“四能”:提高从数学角度发现和提出问题得能力、分析和解决问题得能力
扩展阅读: 高数 向量代数与空间解析几何【练习】同角三角函数的基本关系及诱导公式如何理解一致连续性高中数学思维导图整理高中数学资源大全100G网盘下载链接【线性代数】经典题目讲解 求正交矩阵方法技巧|立体几何中添加辅助线的方法搞定外接球八种模型高中数学导数高考命题回顾高中数学公式整理!!高中数学公式以及概念正弦定理的五种证明方法浅谈教师的备课观数学之美——图形王国简单线性规划知识总结锐角三角函数知识点总结 数学故事——三次数学危机史上最短数学论文:关于欧拉猜想的反例【高中数学】空间向量知识点总结以及题目练习新课标下高中数学课程基本理念与学科核心素养新课改下高中数学的“四基”“四能”高中数学50个二级结论【常考】高中数学课程结构以及课程内容 好文荐读 | 黄翔:从“四基”“四能”到“三会”——一条培养学生数学核心素养的主线中考数学常用公式及性质【总结】教学反思 中学生数学思维障碍成因及突破 高中数学 特殊函数图像汇总高中数学 函数模块全解析 高中数学 圆锥曲线精选试题初中数学 重难点汇总 高中数学 重难点常考点 高中数学知识点归纳总结【精华版】 高中数学 排列组合21中解题方法 中值定理三天王的关系——拉格朗日中值定理、柯西中值定理、罗尔中值定理 【线性代数】 克拉默法则 【高中数学】 导数及其应用小结【高中数学】 解题方法归纳及经典例题解析 【高等数学】Maple Pascal's Triangle 高考数学二轮复习讲义 高考数学三轮复习讲义 上帝掷骰子吗?| 概率统计基础 新青年论文选读|胡晋宾等:从美国《身边的数学》编写看高中课标教材修订 GeoGebra在高中数学的应用 GeoGebra快捷键介绍【高中数学】讨论集合、邻域、区间【高中数学】圆锥曲线11大常考题型【数学】为什么圆是360度? 【高中数学】八种三角函数中的数学思想方法 【高中数学】必修选修重难点 【一个数学难题】:20以内究竟包不包括20? 【高中数学】52种快速做题方法【中考数学】解题中常见的“漏解”情况分析 【高中数学】29条经典考前指导! 如何理解施密特正交化麻省理工牛人解说数学体系 数列研究工具介绍--整数数列在线大全OEIS【高考数学】审题的八大环节【高中数学】圆锥曲线中的最值与范围问题 如何学好高中数学 【高等数学】常用泰勒公式及展开 阿贝尔的坚持 Riemann与Lebesgue积分 什么是“教育教学”(上)【张景中】什么是“教育数学”(中) 【张景中】什么是“教育数学”(下) 【张景中】【数学之美】数学与艺术完美邂逅!改变世界的 17 个数学公式高中数学课程结构与学科核心素养课堂教学改革与教师职业素养的最大公约数——对“课堂教学改革的10大追问”的追加阐述【高中数学】4大思想涉及的20种高频考点全梳理几何画板和勾股定理【高等数学】搞定贝叶斯公式,只需记住这5个字我们为什么要学数学欧拉恒等式,上帝创造的公式非欧几何简介罗增儒:数学解题的四个水平老师,学数学没用!孩子,这篇文章告诉你,学好数学,受用一生!教你用几何画板画繁花曲线 【高中数学】空间向量与立体几何知识点大总结 对于初中数学板书设计的两个启发 分享 解析几何“三步曲”,名师教你用“坐标法”解决三大类常考难题! 分享 小学数学“求图形面积”的10种方法 分享 初中数学必须掌握的几何辅助线技巧! 李永乐:让科学知识成为流行 软件推荐——一款被称为“数学家的软件”的软件 Maple 【初中数学】分享 2020中考函数综合压轴题整理汇总! 【分享】2020年高考数学模拟检测卷附答案,冲刺必备! 【分享】 法向量夹角与二面角大小何时相等?何时互补? 【高中数学】必修1-5常考重难点【高考前的冲刺】高中数学12组答题模板 【高中数学】高考数学如何逆袭 【高中数学·圆锥曲线】(七)再论焦半径【高中数学】易错点整理【分享】【初中数学】中考重难点 【高中数学】9个技巧解决基本不等式问题 前方高能,中考数学考前指导(强烈建议收藏) 【高等数学】2020高考数学最可能考的50道题 分享 【高中数学】初中数学必考公式定律整理 分享【高中数学】近三年高考重难点试题分析(转) 【高中数学】近9年考点分析(转) 【高等数学】近9年考点分析 文科 (转) 【高等数学】立体几何考点(转) 【高等数学】50个公式,50个快速解题法【高等数学】九个技巧解决基本不等式(转)【中考数学】阴影部分面积计算模型大总结 【高考数学】2020高考数学"评分细则"参考发布(转) 【高中数学】高中圆锥曲线重点知识归纳和常用结论 教师教学常用的10个软件 【高中数学】高中圆锥曲线重点知识归纳和常用结论 【高中数学】选做题——极坐标与不等式 【高中数学】23个经典不等式 【初中数学】公式表 【高中数学】知识点表格总结 【高中数学】三角形中的21条结论汇总 【初中数学】压轴题答题技巧与解题切入点分析 【初中数学】数学公式定理总结【高中数学】导数知识总结和导数七大题型答题技巧【初中数学】12张表汇齐初中数学重点知识 2020年深圳中考数学真题解析 【高中数学】解题公式汇总 行是知之始,知是行之成。好的先生不是教书,不是教学生,乃是教学生学。我们要能够做,做的最高境界就是创造。只知学而不知做,就不是真的教育。有行动之勇敢,才有真知的收获。 学习没有白走的路,每一步都算数。
匠心,就是在重复的岁月里,对得起每一寸光阴。
大家共勉。
学习没有白走的路,每一步都算数。
匠心,就是在重复的岁月里,对得起每一寸光阴。
大家共勉。








 本文详细介绍了多种几何体的侧面积与体积计算方法,包括圆柱、圆锥、圆台、棱柱、棱锥、棱台等,并通过典型例题进行解析。此外,还介绍了球体的表面积和体积公式,以及如何应用割补法解决不规则几何体的问题。
本文详细介绍了多种几何体的侧面积与体积计算方法,包括圆柱、圆锥、圆台、棱柱、棱锥、棱台等,并通过典型例题进行解析。此外,还介绍了球体的表面积和体积公式,以及如何应用割补法解决不规则几何体的问题。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








