lingo纳什均衡代码_传统的战略式博弈求解纳什均衡方法——虚拟博弈(Fictitious Play)讲解及其代码...-CSDN博客

本文链接：https://blog.csdn.net/weixin_39895167/article/details/111669796

本文介绍了博弈论中的虚拟博弈（Fictitious Play）方法，这是一种用于求解纳什均衡的传统策略。内容包括虚拟博弈的基本思想，即智能体根据对手历史平均策略选择最优策略，并逐步收敛到纳什均衡。通过石头剪刀布的例子进行解释，指出虚拟博弈仅适用于零和或包含纯策略纳什均衡的常和博弈，且收敛结果可能依赖于初始策略和收益矩阵。文章最后提供了虚拟博弈的Lingo代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

虚拟博弈是博弈论中一种传统的方法，其历史真的非常久远，于1951年被Brown, George W 提出。

其核心思想非常简单，就是利用博弈论中常用的反应函数思想。使每个智能体拥有两个策略集。一个是最优策略集，一个是历史平均策略集。在每一轮博弈的开始，每个均智能体根据对手的历史平均策略集，找到一个最优的针对策略。然后根据历史平均策略和本轮最优策略更新自己的历史平均策略。

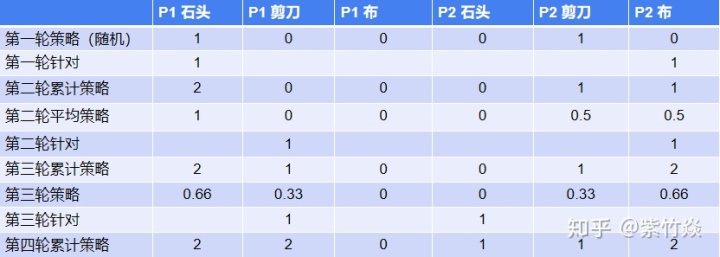
拿石头剪刀布举例子：首先第一轮随机出拳，如果P1石头，P2剪刀。在第二轮时，P1根据P2的历史数据（P2只出了剪刀）得出自己应该出石头，则P1还是出石头，P2根据P1历史数据（P1只出了石头）得出自己应该出布。所以第二轮P1石头，P2布；玩家更新自己的历史策略集P1还是只出了石头，P2有50%的情况出了剪刀，50%的情况出布，以此类推。。。随着迭代的继续，策略会慢慢收敛到纳什均衡。

但是，虚拟博弈并不能解决所有问题。虚拟博弈只能解决零和博弈，或者是包含纯策略纳什均衡解的常和博弈。在常和博弈中如果存在多个纳什均衡，则虚拟博弈收敛的结果会由收益矩阵和初始策略有关，并不能保证收敛到“最优均衡”。此外，虚拟博弈依赖于问题是战略式描述，如果要求扩展式的问题，则一直等到2015年FSP (Fictitious Self-Play) 虚拟自我博弈出现才能处理&#x