重叠面积_初中数学动点难题：数轴上两长方形面积重叠问题再探究

数轴上的动点问题难不难？动点变式题确实特别难？对，特别难，难在要求学生具有超丰富的空间想象力和严谨的思维逻辑力，笔者就在数轴上的动点问题探究变式题二(数据有所修改)继续进行分享，还是用几何图形和代数方法来解题。

如图，长方形OABC的边OA在数轴上，O为原点，长方形OABC的面积为14cm2. OC边长为4cm.

将长方形OABC沿OA所在直线水平移动，移动后的长方形记为O'A'B'C'.若D为线段AA' 的中点，点E在线段OO'上，且OE=1/3OO',求当长方形OABC移动的距离为多少时，D、E两点到原点O的距离相等？

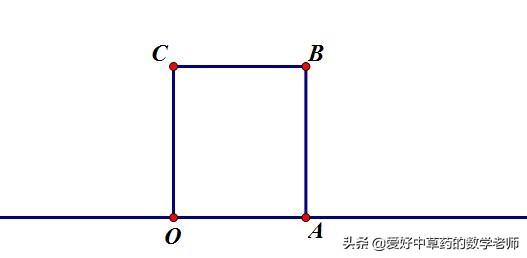
解：由题意可知：

OA=14=3.5cm

题目要求：若D为线段AA' 的中点，点E在线段OO'上，且OE=OO',求当长方形OABC移动的距离为多少时，D、E两点到原点O的距离相等？

一、首先用几何画板进行图形轨迹分析，解决问题：

⑴首先，让长方形OABC向数轴的正方向移动，如图2：

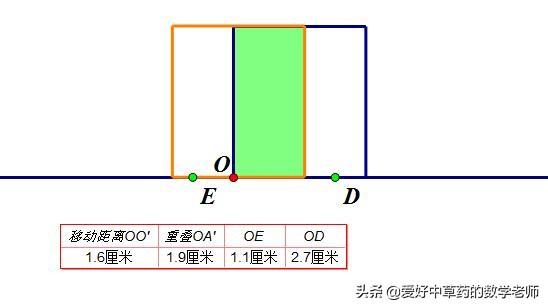
∵ 发现越往右移动，始终OD>OE，∴移动长方形OABC向右移动，得不到OD=OE

⑵要使 D、E两点到原点O的距离相等，我们只有向左移动长方形，得到如下图形：

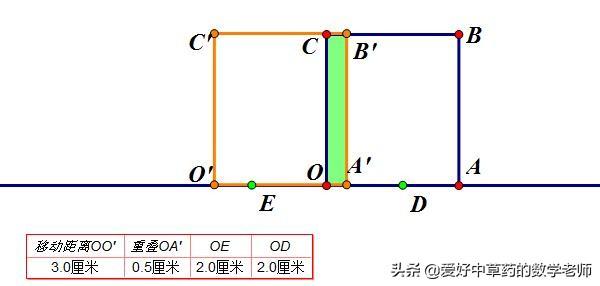
从图表中，我们发现OE=OD时，长方形向左移动3个单位，重叠距离为0.5个单位，相等的距离为2个单位。

∴当长方形OABC移动的距离为3个单位时，D、E两点到原点O的距离相等。

二、使用完几何画板解题，我们用代数形式验证答案的正确性？

解：设移动的距离为x，由题意得

x*2/3=3.5-x+x/2

化简整理得：

7/6*x=3.5

解之得：

x=3

答：略

总结：用代数解题，需要使用分类讨论，分析得到只有长方形OABC向数轴左边移动，才能得到我们需要的结果。

三、探究数轴动点问题三(供读者自行解答)：

如图，已知数轴上A、B两点所表示的数分别为-2和8．(1)求线段AB的长；

(2)若P为射线BA上的一点(点P不与A、B两点重合)，M为PA的中点，N为PB的中点，当点P在射线BA上运动时，线段MN的长度是否发生改变？若不变，请你画出图形，并求出线段MN的长；若改变，请说明理由．(3)若有理数a、b、c在数轴上的位置如图所示：

且d=|a+b|-|-2-b|-|a-2c|-5，试求7(d+2c)2+2(d+2c)-5(d+2c)2-3(d+2c)的值．

PS:

码字不易，欢迎读者在评论区进行评论，您的建议和评论对我创作大于裨益，欢迎转发与关注，谢谢！----爱好中草药的数学老师。