回溯法基本思想_LeetCode刷题笔记（三）--回溯法（DFS）

回溯法，又称深度优先搜索，Deepth-First-Search; 先递归下去，至最深一层，从最深层次开始遍历回溯至第一层;
还有一个叫做广度优先搜索（BFS），先压着不在这阐述了。
既然叫做回溯法，那肯定是步骤中有回溯这一步，说起来简单，代码里是怎么递归至最深一层，然后又怎么回溯上来,两个大大的问号在我这个小菜鸡头上。
上几道题，直接题里找找感觉。

39.组合总和

39.组合总和 给定一个**无重复元素**的数组 candidates 和一个目标数 target ， 找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。
说明： 所有数字（包括 target）都是正整数。解集不能包含重复的组合。
示例 1：
输入：candidates = [2,3,6,7], target = 7,
所求解集为： [ [7], [2,2,3] ]
示例 2：
输入：candidates = [2,3,5], target = 8,
所求解集为： [ [2,2,2,2], [2,3,3], [3,5] ]

class Solution:
    def combinationSum(self, candidates, target):
        '''
        tag:回溯法,选取一个值（append），进行循环比较操作后，pop出去（回到上一步）
        Python3 的 [1, 2] + [3] 语法生成了新的列表，一层一层传到根结点   
        以后，直接 res.append(path) 就可以了；
        基本类型变量在传参的时候，是复制，因此变量值的变化在参数里体现就行，
        所以 Python3 的代码看起来没有「回溯」这个步骤。
        '''
        def dfs(candidates, begin, size, path, res, target):
            if target < 0:
                return
            if target == 0:
                res.append(path)
                return

            for index in range(begin, size):
                # path  =path + [candidates[index]] //思想 
                # path[-1].pop() // （这一步实现需要更多的逻辑判断），直接融合到参数这体现更简洁
                dfs(candidates, index, size, path + [candidates[index]], res, target - candidates[index])

        size = len(candidates)
        if size == 0:
            return []
        path = []
        res = []
        dfs(candidates, 0, size, path, res, target)
        return res

从数组的第一个点，开始挨个遍历，同时并判断target = target-sum大小，小于0，则回溯上一层，重复操作，附个图解释一下。逻辑思路

Analyze:
    Func:
        判断target：
            等于0， res.append(path)
            小于0，返回上一层
            大于0：继续往下遍历
        从第一个元素i=0 in (0,len)开始搜索：
            path = path.append(cand[i])
            设置 target = target - cand[i],回溯调Func
            path.remove(cand[i])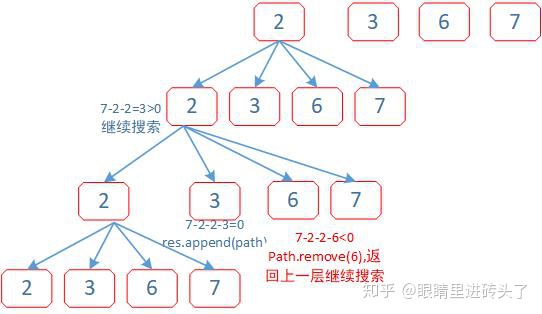

回溯图解：由第一个数开始，逐个往下搜索。大于target，则回溯上来=一层，继续搜索

再附一段JAVA，更清楚的体现了回溯这一步，看完JAVA的代码，小脑袋瓜一下子有了回溯的大体印象

// Java Code  --Java更容易理清回溯法的逻辑
    private void dfs(int[] candidates, int begin, int len, int target,
        Deque<Integer> path, List<List<Integer>> res) {
        // target 为负数和 0 的时候不再产生新的孩子结点
        if (target < 0) {
            return;
        }
        if (target == 0) {
            res.add(new ArrayList<>(path));
            return;
        }

        // 重点理解这里从 begin 开始搜索的语意
        for (int i = begin; i < len; i++) {
            path.addLast(candidates[i]);

            // 注意：由于每一个元素可以重复使用，下一轮搜索的起点依然是 i，这里非常容易弄错
            dfs(candidates, i, len, target - candidates[i], path, res);

            // 状态重置
            path.removeLast();
        }
    }

40 数组总和II

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的每个数字在每个组合中只能使用一次。
说明： 所有数字（包括目标数）都是正整数。 解集不能包含重复的组合。
示例 1: 输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为: [ [1, 7], [1, 2, 5], [2, 6], [1, 1, 6] ]
示例 2: 输入: candidates = [2,5,2,1,2], target = 5,
所求解集为: [ [1,2,2], [5] ]

class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        '''这个题与上面不同，给的数组是包含重复数的，故会出现重复解，需去重。
        '''
        def dfs(cand, tar, path, res):
            if tar <0:
                return
            if tar == 0:
                res.append(path)
                return
            n = len(cand)
            for i in range(n):   # 排序完之后避免在同一层中使用相同的元素
    # tar小于下一个数或(i不是第一个数且前后数相等)时，跳过不执行搜索句，其他条件都执行
                if target >=cand[i] and not(i>0 and cand[i]==cand[i-1]):
                    # candidates[i+1:]从第i+1个数开始搜索
                    dfs(cand[i+1:], tar-cand[i], path+[cand[i]], res)

        candidates.sort() # 先排序（因为需要比较前后一个值是否相同）
        res,path = [], []
        dfs(candidates,target, path, res)
        return res

这一题与上一题不同的点在于，这给的数组是包含重复数的，故会出现重复解，需去重。这里每个数字只能选一次，不能重复选。逻辑思路思考一下i的值。每次dfs回溯传进去的是cand[i+1:]，表示每次都是从i=0开始搜索。

回溯图解：因为不能重复，故排序后，从自己的后一位开始搜索，其他类似上一题

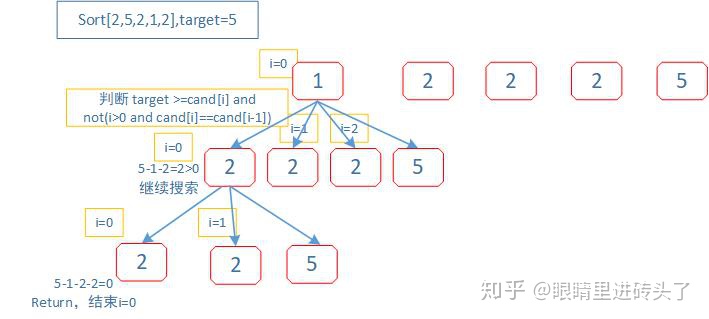
逻辑代码：

Analyze:
    1.因为需要数字去重，故先排序
    2.每次在选择下一个数字时，多进行一步逻辑判断target >=cand[i] and not(i>0 and cand[i]==cand[i-1]):
    DFSFunc:
        判断target：
            等于0， res.append(path)
            小于0，return (返回上一层)
            大于0：继续往下遍历
        从第一个元素i=0 in (0,len)开始搜索：
            path = path.append(cand[i])
            设置 target = target - cand[i],回溯调DFSFunc,此时每次传进来的数组为cand[i:](去重很关键，体会一下)
            path.remove(cand[i])

79. 单词搜索 【回溯】

给定一个二维网格和一个单词，找出该单词是否存在于网格中。
单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些 水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例: board = [ ['A','B','C','E'], ['S','F','C','S'], ['A','D','E','E'] ]
给定 word = "ABCCED", 返回 true
给定 word = "SEE", 返回 true
给定 word = "ABCB", 返回 false
提示： board 和 word 中只包含大写和小写英文字母。

class Solution:
    # 建立一个网格，
    def exist(self, board: List[List[str]], word: str) -> bool:
        m = len(board) # row
        n = len(board[0])  # column

        visited = [[False] * n for _ in range(m)]

        rows = [-1, 0, 1, 0]
        cols = [0, 1, 0, -1] # 上下左右四个方向

        def dfs(x, y, idx):
            """搜索单词
            Args:
                x: 行索引
                y: 列索引
                idx: 单词对应的字母索引
            """
            if board[x][y] != word[idx]:
                return False
            if idx == len(word) - 1:
                return True

            # 先标记
            visited[x][y] = True

            # 找到符合的字母[x,y]处开始向四个方向扩散搜索
            for i in range(4):
                nx = x + rows[i]
                ny = y + cols[i]
            # 新的坐标nx，ny没有越界，且[nx][ny]没有被使用过且在board查找到word[idx+1](回溯在这里)
                if 0 <= nx < m and 0 <= ny < n and not visited[nx][ny] and dfs(nx, ny, idx+1):
                        return True
            # 扩散未搜索对应的字母，释放标记
            # 继续往其他方位搜索
            visited[x][y] = False
            return False

        for x in range(m):
            for y in range(n):
                if dfs(x, y, 0):
                    return True
        return False

逻辑思路

Analyze:
    从给的board中挨个搜索，找到word中第一个字母word[0]在board中的位置：
        if找到,则回溯：
            (假设坐标[1,1,]):则在坐标[1,1]上下左右四方向依次搜寻下一个word[1]的位置（回溯含在搜寻条件中，主要是用于回溯上一个位置。
            ：比如坐标[1,1]上方board[1,2]==word[1],则继续在[1,2]位置往下寻找，否则回溯到[1,1]下方位继续搜寻）

78.子集

【位运算+回溯】
给定一组不含重复元素的整数数组nums，返回该数组所有可能的子集（幂集）。
说明：解集不能包含重复的子集。
示例: 输入: nums = [1,2,3]
输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]

class Solution:
    # 方法一
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = [[]]
        for i in nums:
            res = res + [[i] + num for num in res]
        return res

    # 方法二
    def subsets(self, nums: List[int]):
        res = []
        n = len(nums)

        def helper(i, n, tmp):
            res.append(tmp)
            # print(f"{i},,{tmp},,{res}")
            for j in range(i, n):
                helper(j + 1, n, tmp + [nums[j]])
        helper(0, n, [])
        return res

逻辑分析
这里的回溯指的是每次回到tmp=[]或tmp的上一个状态。

方法二：
Analyze: 这题直接把输出放出来，一下就看明白了
    # 第一层循环helper(0,n,[]), j=0:
    0,,[],,[[]]
    1,,[1],,[[], [1]]
    2,,[1, 2],,[[], [1], [1, 2]]
    3,,[1, 2, 3],,[[], [1], [1, 2], [1, 2, 3]]
    # 第一层中的第二层循环helper(0, n=2, [1]), j=1
    3,,[1, 3],,[[], [1], [1, 2], [1, 2, 3], [1, 3]]  # j=2, heper(2+1,2,[1,3])这里第二层循环结束
    #第一层循环helper(0, n, []), j=1
    2,,[2],,[[], [1], [1, 2], [1, 2, 3], [1, 3], [2]]
    3,,[2, 3],,[[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3]]
    #第一层循环helper(0, n, []), j=2  (第一层循环结束)
    3,,[3],,[[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3], [3]]

90.子集II
同样是不含重复子集，这一题与上一题不同的是给定数组包含重复元素

给定一个可能包含重复元素的整数数组 nums，
返回该数组所有可能的子集（幂集）。
说明：解集不能包含重复的子集。
示例: 输入: [1,2,2]
输出: [ [2], [1], [1,2,2], [2,2], [1,2], [] ] '''

class Solution:
    def subsetsWithDup(self, nums):
        if not nums:
            return []
        n = len(nums)
        res = []
        nums.sort()
        # 思路1
        def helper1(idx, n, temp_list):
            if temp_list not in res: # 判断一下有没有，不够优雅
                res.append(temp_list)
            for i in range(idx, n):
                helper1(i + 1, n, temp_list + [nums[i]])
        # 思路2，这个思路是优雅的
        def helper2(idx, n, temp_list):
            res.append(temp_list)
            for i in range(idx, n):
                # 这个i>idx条件很重要，
                if i > idx and  nums[i] == nums[i - 1]:
                    continue
                helper2(i + 1, n, temp_list + [nums[i]])
        helper2(0, n, [])
        return res

分析: 当涉及到重复元素时,子集要求不重复，那必定是需要先排序，然后再比较前后位元素是否相同,重点就是在if条件判断，其他的思路就与上一题无差别了。

经过这几道题以及基本思想和套路总结，对回溯法有那么点感觉了，你上你也行！

后续持续更新，待续~