平行四边形面积_平行四边形里阴影部分的面积与平行四边形的面积之比是多少？...

如图，平行四边形ABCD的一边AB=12厘米，AB上的高等于8厘米，四边形EFOG的面积等于8平方厘米，则阴影部分的面积与平行四边形的面积之比是多少？

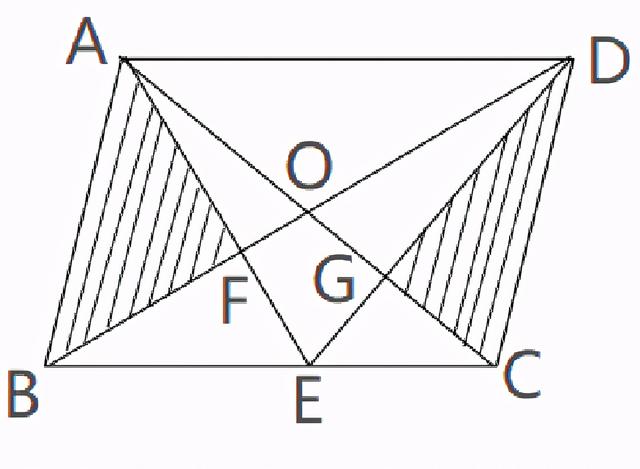
解析：首先我们要知道平行四边形对角线互相平分这个定理，平行四边形两条对角线相交，交点为两条线段的中点。可推出平行四边形里由2条对角线形成的四个三角形面积相等。

平行四边形的面积等于底乘以高，我们可求得S=AB*h=96平方厘米，BOC的面积S1=96除以4=24平方厘米.

我们可以看到阴影三角形ABF和DCG各自处于三角形ABE和DEC内，EFOG就是三角形BOC减去空白三角形BFE和EGC的面积，面积为8平方厘米。

三角形ADE和平行四边形等底等高，所以三角形ADE的面积是平行四边形的面积的一半，三角形ABE和DEC的面积和为四边形面积的2分之1即48平方厘米。

S阴影=SABE+SDEC-(SBFE+SEGC)=48-(24-8)=32平方厘米

即S阴影：S平行四边形=32:96=1:3