前面我们从数值积分的角度推导出龙格库塔法 数值积分公式的推广:龙格库塔法(一)。
这次详细讨论各类龙格库塔法。
4. 龙格库塔法
标准教科书里通常会直接给出如下数值格式:


称  为在节点
为在节点  处的级值,由于共有 s 个级值,故称之为 s 级的龙格库塔 (Runge-Kutta) 法,其系数可以写成下面布切尔表的形式
处的级值,由于共有 s 个级值,故称之为 s 级的龙格库塔 (Runge-Kutta) 法,其系数可以写成下面布切尔表的形式

如果系数满足条件  ,即表格主对角线及其右上角的元素全为 0 时,称相应的方法为显式的龙格库塔法,否则称为隐式龙格库塔法。
,即表格主对角线及其右上角的元素全为 0 时,称相应的方法为显式的龙格库塔法,否则称为隐式龙格库塔法。
现在看来,龙格库塔法其实就是对前面我们用数值积分公式推导的单步法的一种自然推广而已!只是将系数作了进一步的抽象化罢了。科学研究经常干这种抽象假设归纳总结的事情,不是么?
这里顺便插一句,龙格库塔生活的那个年代,由于没有计算机,人们基本靠手算,对于提出像前面那样的隐式格式是无法想象甚至是从内心感到害怕的(注:布切尔在其综述论文【1】中使用了``frightening"这个词)。
实际上,前面提到的显式欧拉法就是最简单的龙格库塔法。历史上,大数学家欧拉构造显欧拉法的想法其实非常简单,就是用分片的直线段来逼近真解(细究起来,个人感觉有限元法的最原始思想其实应归功于老祖宗欧拉,哈哈)。可惜精度只有一阶,因此人们希望构造新的精度更高的数值方法。
继欧拉之后,龙格和库塔,分别于1895年及1901年构造了精度更高(2阶到5阶)的显式数值格式,采用了对不同节点处切线斜率的某种加权平均作为下一步“前进方向”(“切线斜率”本质上刻划了方向)的逼近思想。这种精度更高的格式可以看成是对显式欧拉法的升级推广,“龙格库塔法”的名字也由此而来。龙格和库塔给人们提供了构造高精度数值格式的新思路,这个意义是相当重大的。
从欧拉1768年提出折线法到这一想法出现,竟然用了127年!如今看来,从数值积分公式推广和应用的角度,结合对系数的抽象化理解, 岂不是显得更自然、更易于接受么?
阶条件
通常为了便于分析数值方法的阶(特指局部截断误差的阶),我们还需假定: 对 

注意,上述假定条件并非必须。但有了上述假定,所有代数阶条件可以用一个统一的简洁而优美的根树公式来表达。而如果没有上述假定,在研究较高阶局部截断误差项时 -- 正如布切尔在文献【1】中所指出的那样 -- 一旦考虑的误差阶数超过4阶,就算是一维方程组(即 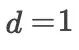 )情形,泰勒展开式的高阶项也会使人困惑 (get confused) 且前面的能够用统一公式表达的阶条件已显得不够充分(注:胡塔考虑过直到6阶的情形)。笔者推测,他的意思可能是问题太复杂了,理不清头绪。
)情形,泰勒展开式的高阶项也会使人困惑 (get confused) 且前面的能够用统一公式表达的阶条件已显得不够充分(注:胡塔考虑过直到6阶的情形)。笔者推测,他的意思可能是问题太复杂了,理不清头绪。
另一个合理的解释是,任何一个非自治方程组(注:这里的“非自治”是指右端函数 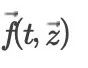 显式地依赖于时间变量)均可以先转化成一个自治方程组再来求解。转化的方法如下:我们可以在原微分方程组的基础上添加一个显而易见的方程
显式地依赖于时间变量)均可以先转化成一个自治方程组再来求解。转化的方法如下:我们可以在原微分方程组的基础上添加一个显而易见的方程 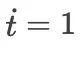 ,使得原微分方程组(非自治的)升维成
,使得原微分方程组(非自治的)升维成 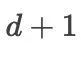 维的新的微分方程组(此时可看成自治的)。将龙格库塔法用于新的方程组。此时,要求精确积分刚添加进来的简单方程是合理的(因为右端函数为常数1,恰好是可以求出解析解的情况)。具体地讲,
维的新的微分方程组(此时可看成自治的)。将龙格库塔法用于新的方程组。此时,要求精确积分刚添加进来的简单方程是合理的(因为右端函数为常数1,恰好是可以求出解析解的情况)。具体地讲, 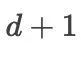 维的龙格库塔数值格式中含有下面的式子
维的龙格库塔数值格式中含有下面的式子
 比较两边后即得到上述条件。
比较两边后即得到上述条件。
通过将 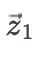 在
在  处作泰勒展开,并与精确解的泰勒展开式作比较,易知
处作泰勒展开,并与精确解的泰勒展开式作比较,易知

是龙格库塔法具有1阶精度(即局部截断误差为 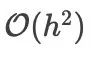 )的充分必要条件。欲使方法达到二阶精度,则需要另外加上下面的约束条件
)的充分必要条件。欲使方法达到二阶精度,则需要另外加上下面的约束条件

更高阶的阶条件可以继续进行泰勒展开得到,比较繁琐。布切尔发现了泰勒展开式的一般性规律,将展开式与根树图一一对应,从而可以方便地利用根树图直接写出所有的代数阶条件,这里不再详细介绍。
显式龙格库塔法
显式的最大好处主要还是计算快,不需作迭代,它主要适用于非刚性问题的数值计算,但对于刚性问题不合适,数值稳定性很差。
关于稳定性,针对不同程度的刚性问题提出了很多概念,A稳定,L稳定,B稳定,代数稳定…… 一般显式格式表现都很差。舒其望等人提出了强稳定性的显式龙格库塔法 (布切尔曾在一些论文里也提到过舒老师的工作),比一般的显式龙格库塔法稳定性要好。
前面介绍过1阶-2阶的显式法:
ODE 数值方法(1):方法简介
ODE 数值方法 (2) :截断误差和二阶方法
ODE 数值方法(3):截断误差分析
最常用的显式 4 阶龙格库塔法是库塔 1901 年构造的。下面是方法和其示意图

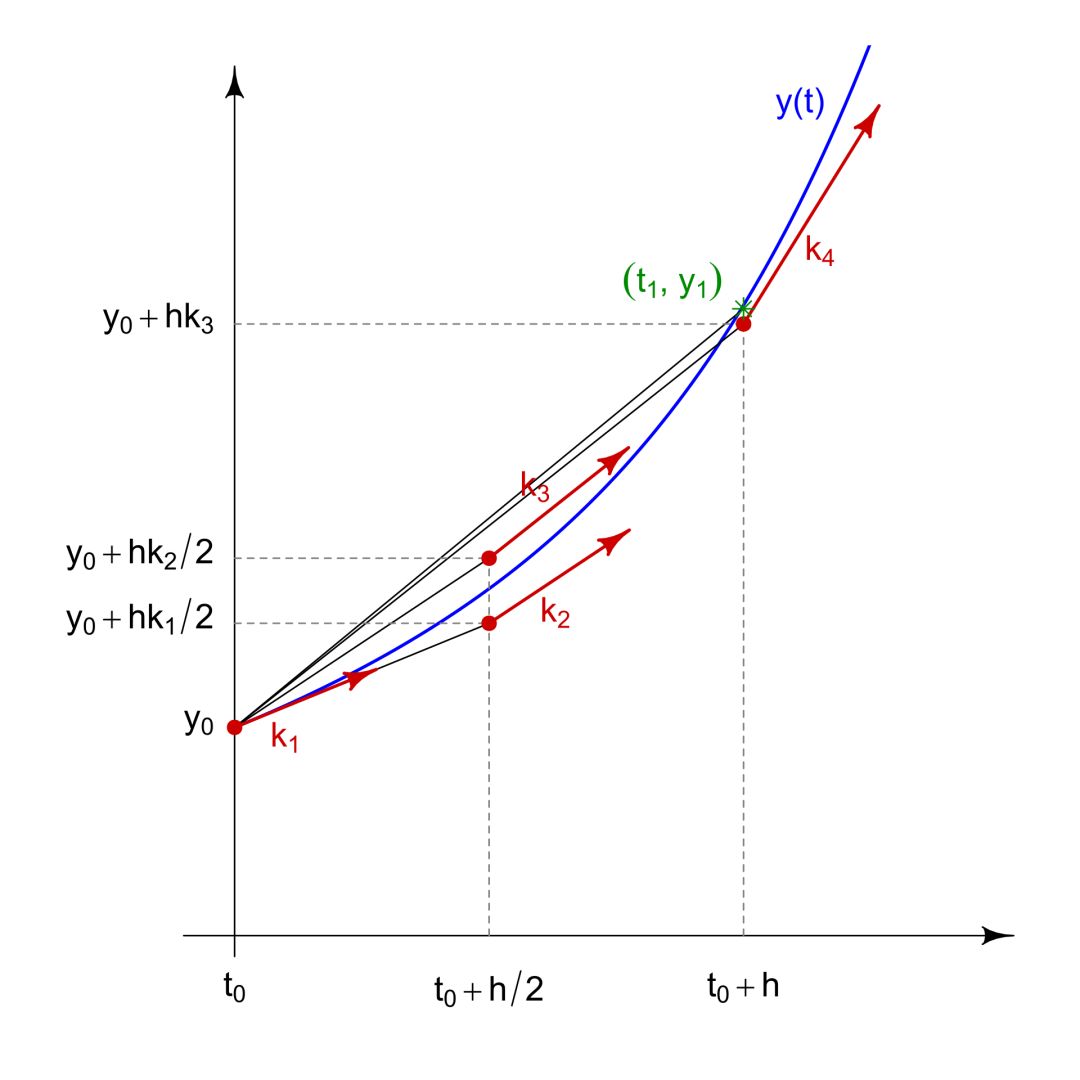
关于显式格式,布切尔、库珀等人利用代数方法深入研究了格式构造过程中存在的阶障碍现象【1,2】,但至今没有彻底解决。
研究表明,对于构造阶为 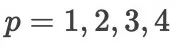 的显式格式,需要的最少级数为
的显式格式,需要的最少级数为 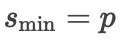 ,而当
,而当 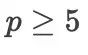 时,
时,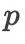 级
级 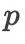 阶精度的显式龙格库塔法是不存在的.
阶精度的显式龙格库塔法是不存在的.
高于 4 阶精度的格式需要数目更多的级值 (即 s 要足够大) 才行。随着 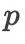 的增大,所需的最少级数
的增大,所需的最少级数 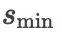 呈现毫无规律的现象。
呈现毫无规律的现象。
比如
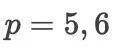 时,需要的最少级数为
时,需要的最少级数为 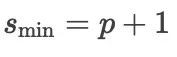 ,
,当
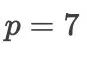 时,
时, 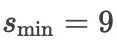 ,
,而当
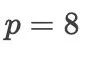 时,
时, 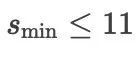 ,
,而
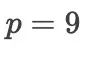 的情况,目前没人考虑。
的情况,目前没人考虑。
海尔(他的儿子曾于2014年获得菲尔兹奖,虎父无犬子啊)考虑了阶 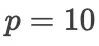 的显式格式,他绕过了1205个非线性代数联立方程组的直接求解,构造了一个
的显式格式,他绕过了1205个非线性代数联立方程组的直接求解,构造了一个 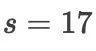 级的显式格式(是不是用的最少级数,目前还不能确定)。
级的显式格式(是不是用的最少级数,目前还不能确定)。
对于构造一般的 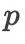 阶精度的显式格式,最少的级数
阶精度的显式格式,最少的级数 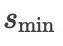 应该是多少?至今没有答案,连猜想都无人提出。
应该是多少?至今没有答案,连猜想都无人提出。
不过,对于 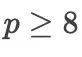 ,库珀(Cooper)与弗纳(Verner)于1972年得到了一个上界估计
,库珀(Cooper)与弗纳(Verner)于1972年得到了一个上界估计 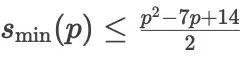 . 布切尔则于1975年给出了一个关于下界的估计式(较复杂,从略)。
. 布切尔则于1975年给出了一个关于下界的估计式(较复杂,从略)。
实践表明,它们都不是最优的上下界估计(从 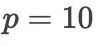 的情形即可看出这一点)。这应该算是在计算数学领域中出现的一个极其困难的“纯数学”问题,其难度可能并不亚于数论中的任何一个困难猜想——至少连关于其终极结论的猜想都还不存在。当然,如果单从构造算法主要用于实际计算的角度来看,解决这个问题可能并无多大实际意义。
的情形即可看出这一点)。这应该算是在计算数学领域中出现的一个极其困难的“纯数学”问题,其难度可能并不亚于数论中的任何一个困难猜想——至少连关于其终极结论的猜想都还不存在。当然,如果单从构造算法主要用于实际计算的角度来看,解决这个问题可能并无多大实际意义。
由于布切尔的工作,尽管目前我们可以很方便地写出阶条件,但构造高阶精度的显式格式通常需要求解较繁琐的关于阶条件的超定非线性代数系统,令人望而却步。
另一个有趣且值得一提的事实是,龙格库塔法可以构成一个群(布切尔群),相应的布切尔群理论与Hopf代数及量子场论具有着惊人的紧密联系【5】。
隐式龙格库塔法
相对于显式格式,高阶精度的隐式格式比较容易构造,可以借助于布切尔 1964 年提出的简化阶条件或其他方法(比如前面的配置法),绕过繁琐的关于一般性阶条件的非线性代数系统的求解。
一个比较成熟的构造方法是利用海尔和万纳提出的 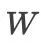 -变换技巧【4】. 另一种巧妙的方法就是我们科研团队的正交多项式展开法【8】(最近又有新的结果待发表,此处给自己顺带插播一个小广告,嘿嘿)。
-变换技巧【4】. 另一种巧妙的方法就是我们科研团队的正交多项式展开法【8】(最近又有新的结果待发表,此处给自己顺带插播一个小广告,嘿嘿)。
此外,很多学者在龙格库塔法解的存在性、收敛性、稳定性 (线性和非线性稳定) 及数值实现方面也作了大量研究工作,这里不再详述。
5. 结尾
时至今日,应该说龙格库塔法已经发展到相当完善的地步了。这里值得一提的是,由于我国著名计算数学家冯康先生自上个世纪八十年代初【3】系统提出了哈密尔顿辛几何算法,龙格库塔法得以在新时期新领域里找到新的价值,并获得了新的发展。
1988年,由桑兹塞尔纳 (Sanz-Serna)、拉萨尼 (Lasagni)、苏里斯(Suris) 三人独立提出并发表了保持辛结构 (symplectic structure) 的龙格库塔法所满足的代数条件【5】,直接推动了辛龙格库塔法的产生和发展。冯康课题组成员孙耿教授在构造辛(分块)龙格库塔法方面有较系统和深入的研究【6,7】,这进一步极大地丰富了龙格库塔法的理论体系。
龙格库塔法在未来是否还会有新的突破和重大发展,值得大家共同向往和猜测。
参考文献
【1】J.C. Butcher, G. Wanner, Runge-Kutta methods: some historical notes, Appl. Numer. Math.22 (1996), 113-151.
【2】J.C. Butcher, The Numerical Analysis of Ordinary Differential Equations: Runge–Kutta and General Linear Methods, John Wiley & Sons, 1987.
【3】K. Feng, On difference schemes and symplectic geometry, in: Proceedings of the 5-th Inter., Symposium of Differential Geometry and Differential Equations, Beijing, 1985, pp.42–58.
【4】E. Hairer, G. Wanner, Solving Ordinary Differential Equations. II: Stiff and Differential-Algebraic Problems, Springer Series in Computational Mathematics, second ed., vol. 14, Springer-Verlag, Berlin, 1996.
【5】E. Hairer, C. Lubich, G. Wanner, Geometric Numerical Integration: Structure-Preserving Algorithms For Ordinary Differential Equations, Springer Series in Computational Mathematics, second ed., vol. 31, Springer-Verlag, Berlin, 2006.
【6】G. Sun, Construction of high order symplectic Runge–Kutta methods, J. Comput. Math.11 (4) (1993), 250–260.
【7】G. Sun, A simple way constructing symplectic Runge–Kutta methods, J. Comput. Math.18(2000), 61–68.
【8】W. Tang, Y. Sun, Construction of Runge–Kutta type methods for solving ordinary differential equations, Appl. Math. Comput.234 (2014), 179–191.
作者简介

唐文生,长沙理工大学数学与统计学院, 讲师
研究兴趣:哈密尔顿辛几何算法.
近年来,基于正交多项式展开技巧发展了连续级算法的较一般性构造理论,并将之用于动力系统保结构算法的研究,提出了构造几类几何积分子的全新方法. 首次发现利用数值通量的不同选取可以构造不同的保持辛结构的间断Galerkin方法,证明了方法的超收敛性,并建立了其与连续级算法的内在联系。主持并完成国家自然科学基金青年项目1项,湖南省教育厅项目1项。
感谢
本人于2018年10月-2019年3月受国家留学基金委资助访问加州大学欧文分校的陈龙教授,此科普短文撰写于访学期间。在此特别感谢陈教授对本文写作的指导和建议。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








