二元函数对xy同时求导_微积分-7.关于三角函数、极坐标系与参数方程

到目前为止，我们都只讨论了平面直角坐标系下的函数。

我们知道，牛顿切入微积分的角度，是为了研究现实世界中的物理运动。假如把函数看作是点

随着时间

的运动轨迹，可以发现，平面直角坐标系，更易于描述平移类的运动；而在涉及到旋转类的运动，直角坐标系就体现出了它的局限性。

比如，当我们想要描述，一个直径为大圆直径四分之一的小圆在大圆内部滚动时，小圆上一点的运动轨迹：

内摆线

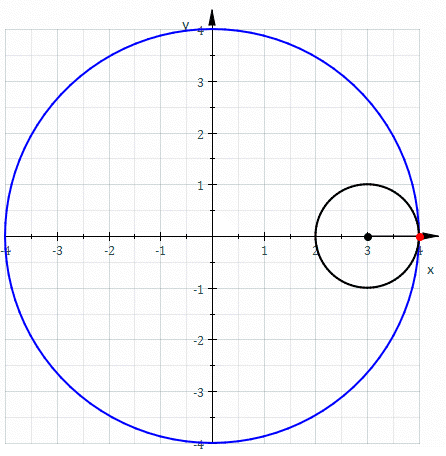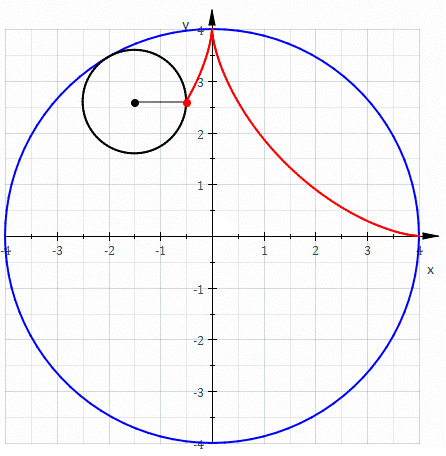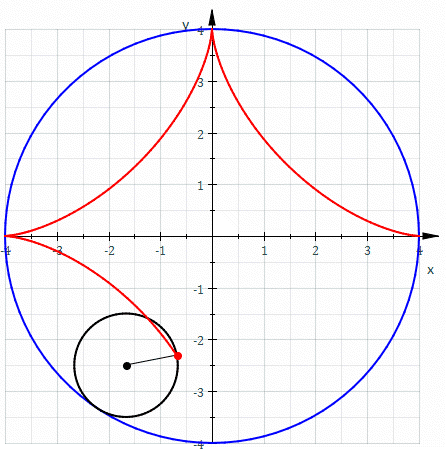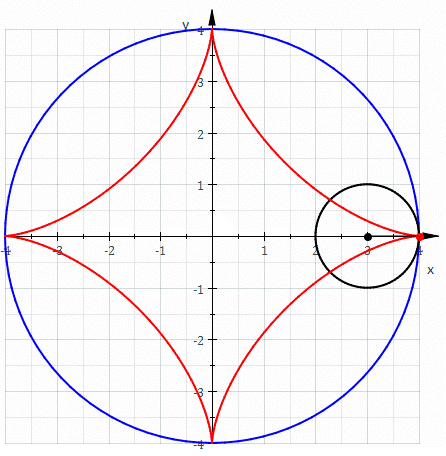
在直角坐标系中，写出该点的运动轨迹，其坐标方程将会是：

首先，它不是一个常规的显函数，对于隐函数，我们无法直接对它的函数性态进行研究；

其次，假如强行的将它解出为

关于

的显函数，由于其特殊的幂次关系，解出后的函数表达式将会异常的复杂，使得我们也几乎难以对它做常规的求导、积分类的运算和研究。

然而，涉及圆、旋转运动以及旋转体等等的这一类问题，在我们的现实世界中却随处可见，比内摆线更为复杂的旋转类相关的坐标方程更是比比皆是。从小小齿轮的转动，到车轮的滚动，再到宇宙天体的运动；从圆柱、圆锥到车削机床对于各种不规则旋转体的高精度加工。

因此，为了解决这一大类关于圆与旋转的问题，我们引入了极坐标系；而三角函数就是架立在直角坐标系与极坐标系之间的桥梁。

---

三角函数系

先从平面直角坐标系上，以原点为圆心的圆，以及圆上一点的坐标与圆心构成的直角三角形开始复习：

若圆上一点

，有圆心角

，则有：

正弦

，余弦

，正切

接着是三个对应的倒函数：

余割

，正割

，余切

以及这六种三角函数对应的反三角函数，在直角坐标系的一个单位圆内构造出所有这些三角函数如下图所示：

三角函数对应的几何意义

正弦函数图像的与圆周运动的对应过程

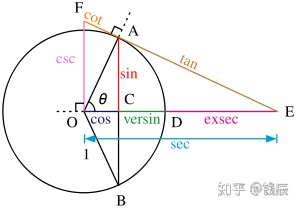
我们可以将一整类在表达式中带有三角函数的函数统称为三角函数系。三角函数系为我们提供了另一个全新的看待函数图像的视角，即将图像看作是点随时间的运动轨迹。

随着学习的深入，我们会逐渐的发现：以多个不同的角度看待分析同一个问题，这样的思维方式是数据学习中建立不同知识点乃至不同领域之间联系的关键。

---

参数方程

现在，回到正弦函数：

将它解出

，则有：

从这个函数表达式中可以看出，我们可以构建出另一个坐标系，在这个新的坐标系中，围绕原点

，以圆心角

与距离圆心的距离

作为坐标参数，则直角坐标系中的纵标轴值

就可以被唯一的映射至这个新的坐标系中。

这个新的坐标系就是极坐标系。

有了极坐标系之后，再来看直角坐标系下的圆方程：

就可以被转化为极坐标系下的一组方程：

在直角坐标系无法直接建立

关于

函数关系，但通过极坐标系的映射，两者可以同时与第三个共同参数（在给定圆的半径

的情况下，即有共同参数

）建立函数关系，从而组成一个方程组，这种方程组就叫

参数方程。

有了参数方程，原本在直角坐标系下难以研究计算的问题，就变得非常简单，例如：

求导

，对分子分母同时除以

，则有：

原本对复杂隐函数的求导计算，就被转化为了对参数方程中对两个简单显函数各自求导的过程：

现在再来试着求解开篇提到的星形线方程：

我们可以先利用圆的方程来进行类比：

则与圆的参数方程相对应的有：

，即可得参数方程：

对其求导，即有：

---

三角函数系区别于普通初等函数，就在于它们两个极其重要的特质：

1. 以轨迹运动角度出发而显现出的周期性；
2. 从极坐标系映射出发而显现出的相互转化性。

也因此，三角函数系的积分在一元函数积分中是极其特殊且重要的一整类问题。这也是我想把它独立出来作为一章来介绍的原因。

周期函数的特性

我们先来研究一下广义的周期函数：

有以

为周期的可积函数

，它在一个完整周期上的积分为：

若求长度为

的任意起止点区间上的积分

首先，依据定积分的区间可拆性，对它进行拆分：

对

部分，使用换元法，令

，则有：

带入积分：

又根据周期函数的特性以及改变变量字母的积分不变性，有：

带回原式，则它与第一部分刚好是被积函数相同、区间相反的定积分，故其和恰为0：

这个结论表明：对于周期函数，只要定积分的区间间隔是一个周期，那么无论区间的起止位置在何处，它总是等于由0开始的一个完整周期内的积分。

这也是一个相当符合我们直觉感受的结论，如图所示：

滑动视窗的宽度只要为一个周期，则其中的部分必然能够拼出一个完整的圆

华里士公式

求

首先，可以将其看作：

根据分部积分公式

，有：

其中

，故有：

又有三角函数的基本性质

，可得：

这时，式子中重新出现了原积分：

若我们设

，则有：

利用这个递推关系，可得：

由此可推：

若

为偶数：

若

为奇数：

这就是华里士公式，用相同的推导方式易推出

与

的计算公式是一致的。

利用三角函数系的转化性进行换元

例1：求

在遇到平方加减带根式的结构，常规的思路就会往三角函数系的方向思考。因为三角函数系中各个三角函数之间的转换易于让我们将根式去除。

令

，在第一象限内，有

由

与

均为偶函数可知

亦为偶函数，故有：

进行换元带入：

即有：

这两部分，就可以各自使用华里士公式：

，答案为：

例2：求

如果使用分部积分法，也可以做，但是过程较为复杂，直接采用上一篇文章最后提到过的区间再现公式

可得：

又因三角函数的性质

，则有：

由此实现了积分的再现，故有：

此时要注意，华里士公式的直接使用必须是在区间

内，而此处的区间为

，故需要对华里士进行区间推广：

令

，则有：

由

为偶函数得知：

于是，便可以使用华里士公式得：

例3：求

在观察函数没有特别明显的变形手段时，尝试直接令

，则有：

故原式变为：

由分部积分公式

可对它进行变换：

这样，我们就将原本不易计算的微元

转换至了被积函数中。

接着，由基本求导公式

以及三角函数性质

，故原式后半部分可转换为：

最终得：

，要记得回带

---

本篇我们对三角函数系、极坐标系做了简单的探讨。至此，在一元函数积分的计算中，我们手里有了定义、性质、区间再现、两类换元法、分部积分、有理函数积分以及华里士公式等工具。

在积分世界的旅程中，有了一个很好的开始。