本文介绍了解决立体几何中外接球问题的高效方法，特别是针对圆柱外接球模型。通过识别模型并应用特定公式，可以简化求解步骤，无需复杂作图。内容涵盖直棱柱、垂棱锥和侧面垂底四棱锥的外接球问题，强调了正弦定理在求解半径中的应用。
题记： 立体几何压轴小题，基本上无论哪个省份，都会十分宠幸“几何体的外接球问题”。那么，倒霉的，看似就是我们这些广大高三狗了。
而这类问题你通常会想到：
❶ 画出球体、标明球心
❷ 画出球的内接几何体
❸ 寻找突破口建立方程。
以上的方法可以说是“通法”，但，并不好用！因为很多人空间感略差，而另外一些人就算空间感不错，最后可能依然面临找不到关系（因为找嘛，考察的是眼力，看走眼总是很正常的）。
那今天我告诉你，这类题80%以上（夸张的说法，确实没统计过，但真的很频繁。）都不用画图，只需要2步搞定：
❶ 识别模型
❷ 代入公式
就可以轻松求出外接球半径
本节教给你的就是这80%中最常用到的第1个模型——圆柱外接球模型。
一、题型描述
几何体的外接球问题： 题目中涉及几何体外接球体，或者球内接几何体，再或者球面上有几个点围成几何体，这类题型称之为几何体的外接球问题。
二、技巧讲解
以下这幅图，大家应该都能看懂：一个底面半径为
这里我要让你明白公式 “
Part 1. 直棱柱的外接球
如果我们对圆柱上下底面对应位置处，取相同数量的点，比如都取三个点，如图所示：
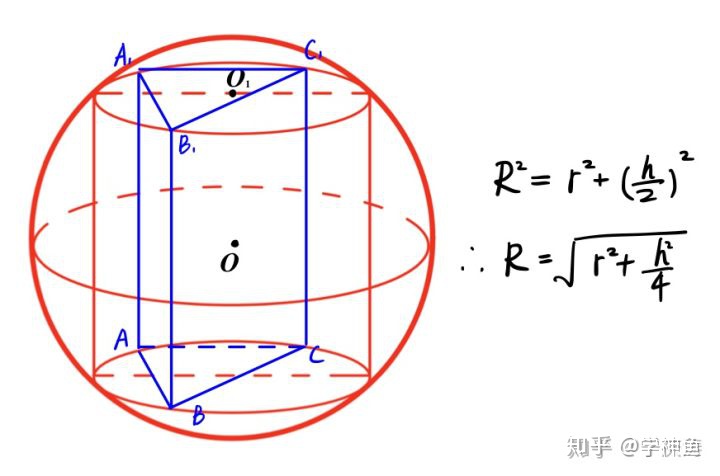
我们可以得到（直）三棱柱，它的外接球其实就是这个圆柱的外接球，所以说直棱柱的“外接球求半径”符合这个模型。
在这里棱柱的高就是公式中的，而棱柱底面外接圆的半径则是公式中的
。
至于怎么求底面外接圆半径
哦对了，斜棱柱怎么办？ 斜棱柱没有外接球，有兴趣的自己尝试找到原因。
Part 2. 垂棱锥的外接球
我们再继续，如果我把刚刚那个三棱柱上面的
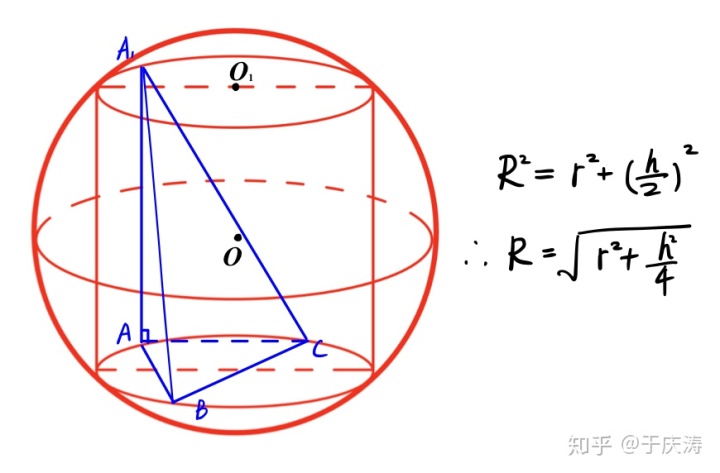
这个三棱锥的特点是
那条竖直棱就是公式中的
，而底面
的外接圆半径是公式中的
。
Part 3. 侧面垂底的四棱锥的外接球
题目还喜欢这么干：
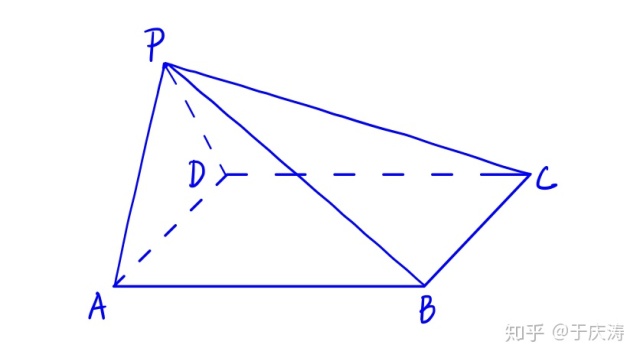
这种类型题目考的够多的了吧！而你，是不是每次都傻傻的画球？其实我告诉你，
它！非！常！符！合！圆！柱！外！接！球！模！型！
接着看，当我对第二幅图中的三棱柱
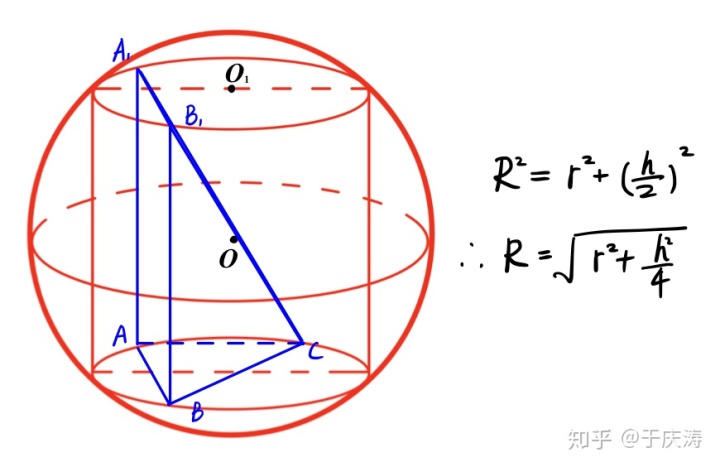
没错！这就是刚刚那个四棱锥放倒了！ 它的特点是：底面
再看这个四棱锥：
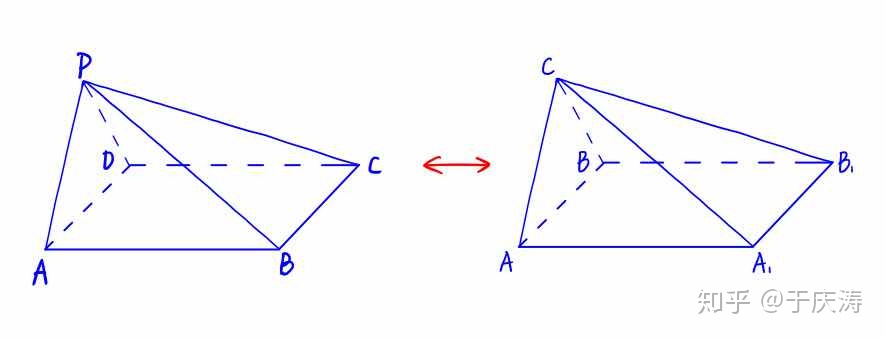
我们知道，这里的为
的外接圆半径，
为
或
的长。
让我们总结一下：
圆柱外接球模型
适用于：
❶ 圆柱——
❷ 直棱柱——
❸ 一根侧棱⊥底面的锥体——
❹ 一个侧面⊥矩形底面的四棱锥——
那么接下来第二步就是找到
正弦定理。正弦定理。正弦定理。
可以说，正弦定理求外接圆半径这种方法，咱们基本上只在高一提及过，后来就很少用到它！其实，几乎整个高考也就此处——「外接球题型」可以用它来求那个
讲解如图：
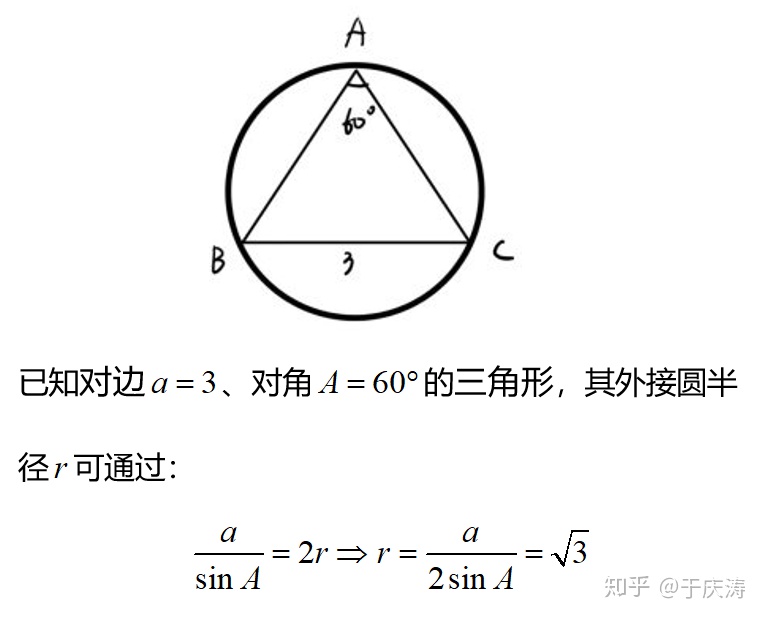
当我们求出
来，我们秒杀几道：
例1. 直三棱柱的六个顶点都在球
的球面上，若
，
，
，则球
的表面积为
A.B.
C.
D.
![]()
学神鱼解析：直棱柱的外接球符合圆柱外接球模型：底面
所以
所以
所以球体表面积：
例2. 点均在同一球面上，其中
是正三角形，
⊥平面
，
，则该球的体积为___________.
学神鱼解析：由题
所以
所以球的体积
例3. 已知四棱锥的顶点都在球
上，底面
是矩形，平面
平面
，
为正三角形，
，则球
的表面积为
A.B.
C.
D.
![]()
学神鱼解析：由题，四棱锥
所以
所以球体表面积
以上，就是本节课程的全部内容。希望能够帮助到你！
<完>
PS：在这里，感谢@烦躁的雅女同学对本节课程的首个赞赏！
如果觉得本文对你有帮助，请点赞收藏，以便你能第一时间找到~~~
更多前往公众号：jslxcn（精师良学）、hitsir（学神鱼）
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
