指数函数中x的取值范围_指数函数和对数函数

1.大纲要求

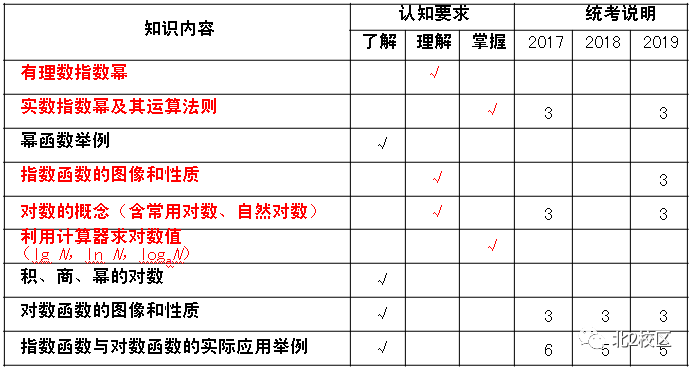
2.应知应会

(1)实数指数幂

①指数幂与根式

 ②实数指数幂及运算法则

        a^m×aⁿ=a^m+n

        (a^m)ⁿ=a^m×n

        (ab)^m =a^m×b^m

(2)指数函数

①指数函数

        y=a^x

②指数函数的图像

        值域：(0， ∞ )

        特殊点：图像过(0，1)点

        函数增减性：当a>1为增函数；0

(3)对数

①对数及性质

        a^b = N 与 b=log_aN 的对应关系。

        b=log_aN  

        特殊情况：log_a1=0；log_aa=1；N>0(0和负数没有对数)

②常用对数(底为10)和自然对数(底为e)

        log₁₀N记为lgN

        log_eN记为lnN

③积、商、幂的对数

        lg(M×N)=lgM+lgN

        lg(M/N)=lgM-lgN

        lgMⁿ =nlgM

(4)对数函数

①对数函数

        y=log_ax

②对数函数的性质

        ◆函数的定义域为(0，+ ∞ )，值域为R；

        ◆当x=1时，y=0 ;

        ◆当a>1，函数为增函数；当0

3.历届统考真题

(1)客观题

序号	题干	参考答案
1	计算4-1=()   A．4    B．3    C．-4    D．1/4	D
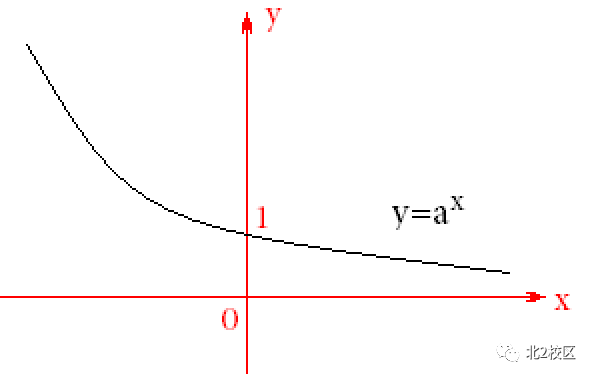
2	右图是指数函数y=ax的图像，则a的取值范围是()。   A.(1，+∞)   B.(0,1)   C.(-∞，0)   D.  R	B
3	将32=9写成对数式是()   A.log32=9   B. log39=2   C. log23=9   D. log29=3	B
4	函数y=log3x的图像必过点()。   A. (0,0)   B. (0,1)   C. (1,0)   D. (1,1)	C
5	“以a为底x的对数等于y”记作()   A. y=logax   B. x=logay   C. x=logya   D. y=logxa	A
6	下列运算中，正确的是()	C
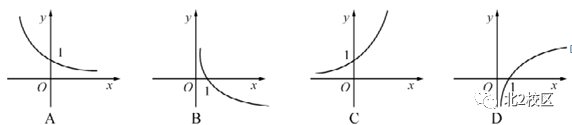
7	函数y=log3x的大致图像为(  )	D
8	若loga2=1，则a的值是(   )	2

(2)主观题

序号	题干	参考答案
1	计算81/3×(√2)2-(√13 -1)0+(lg5+lg2)	原式=2×2 - 1 + lg10 =4 - 1 + 1 =4
2	计算：log22 + (π-1)0 + 3×3-1	原式=1+1+1     =3
3	求值：1/9 × (-3)2 + 2÷(√5 - 1)0 - log39	原式=(1/9)× 9 +2/1 – log332     =1+2-2log33     =3-2     =1

凉山州职业技术学校北2校区