mysql选择投影连接_MySQL入门，第六部分，关系代数

关系代数是一种集合操作为基础过程化查询语言，特点：运算对象是关系，运算结果亦为关系

一、关系代数的特点

运算对象：关系

运算结果：关系

运算符：四类

集合运算符

专门的关系运算符

算术比较符

逻辑运算符

二、关系代数运算符

运算符类型

运算符

含义集合运算符

∪

并

集合运算符

-

差

集合运算符

∩

交

集合运算符

×

广义笛卡尔积

比较运算符

＞

大于

比较运算符

≥

大于等于

比较运算符

＜

小于

比较运算符

≤

小于等于

比较运算符

＝

等于

比较运算符

≠

不等于

专门的关系运算符

σ

选择

专门的关系运算符

π

投影

专门的关系运算符

⋈

连接

专门的关系运算符

÷

除

逻辑运算符

¬

非

逻辑运算符

∧

与

逻辑运算符

∨

或

三、运算规则

1.集合运算规则

将关系R, S看作是元组的集合，进行交、并及差集合运算，必须具备下列条件：

R和S的模式必须相同

R和S的属性顺序也相同表达式

操作类型

含义R ∪ S

并

R、S两者中元组的集合，一个元素在并集中只出现一次

R ∩ S

交

同时存在于R和S中的元组的集合

R – S

差

在R中存在，而在S中不存在的元素的集合

R × S

笛卡尔积

R(n目p元组)，S(m目q元组)；运算得到的新关系中有(n+m)个目(p×q)个元组

解析：

广义笛卡尔积运算：

2.专门的关系运算符

表达式

操作类型

含义

备注

举例σ c (R)

选择

在关系R上选择满足条件C的元组，构成一个新的关系。新关系是R的子集，模式与R相同

条件 c 是一个逻辑表达式，表达式中可以使用比较运算符和逻辑运算符

σ name = '小明' (Student)

π A1,A2,…,An (R)

投影

从关系R产生一个只有R的某些列的新的关系

新的关系中含有旧关系的A1,A2,…,An 列

π name,age (Student)

R⋈ AθB S

θ连接

从两个关系R,S的广义笛卡尔积中选择属性间满足一定条件的元组；记作S⋈R(AθB)

A为包含R中的属性的表达式，B为包含S中的属性的表达式，θ通常为关系比较符；

等效于σ AθB (R×S)

Student ⋈ sGPA≥cGPA Company

R⋈ A=B S

等值连接

当比较运算符θ 为 = 时的θ连接

A为包含R中的属性的表达式，B为包含S中的属性的表达式；

等效于σ A=B (R×S)

Student ⋈ sGPA=cGPA Company

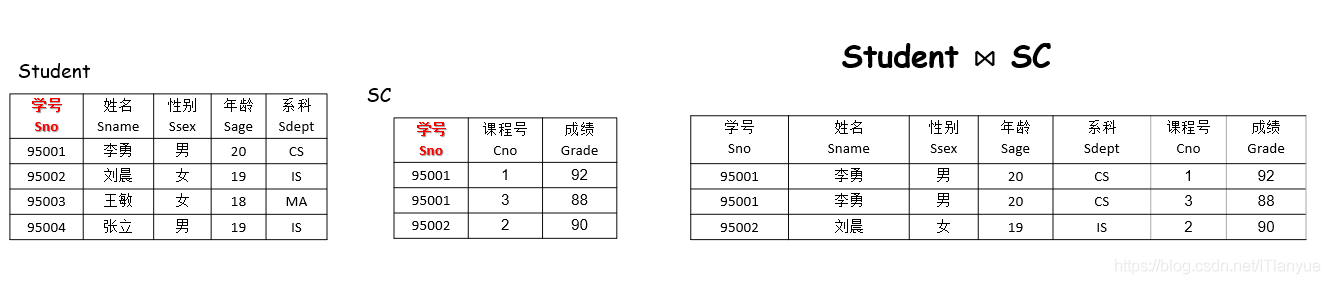
R⋈S

自然连接

一种特殊的等值连接。两个关系中进行比较的分量必须是相同的属性组。在结果中把重复的属性列去掉

Student ⋈ GPA

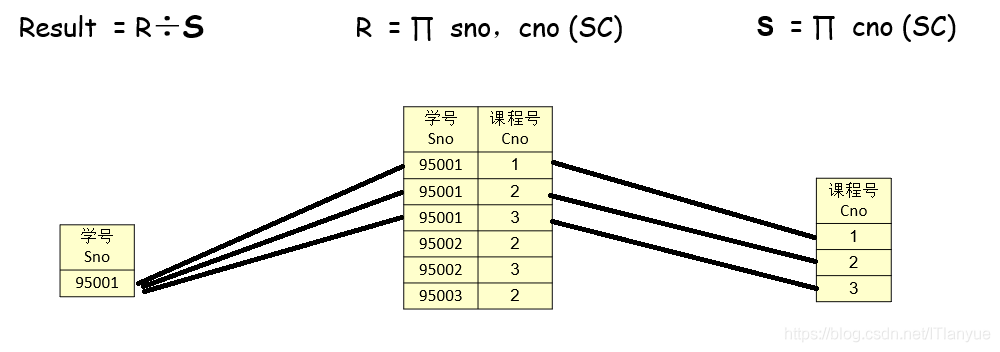
R÷S

除

详解见本文最后

详解见本文最后

详解见本文最后

解析：

自然连接：

除法运算：

=======================================================================================================

为什么把这个分支知识点放到最后单独来说呢？因为它的概念确实是比较抽象的，单独靠一个表格确实无法深入的理解，下面我们一步一步来了解什么是关系代数中的除运算

(1)象集

关系R(A，Z)

A和Z为关系R的属性，a是属性A中的分量值

a在R中的象集：R中在A上值为a元组在Z属性上对应分量的集合

例如：

(2)除

首先我们来看一下官方定义：

除运算是同时从关系的水平方向和垂直方向进行运算。给定关系R(X，Y)和S(Y，Z)，X、Y、Z为属性组。R÷S应当满足元组在X上的分量值x的象集Y，包含关系S在属性组Y上投影的集合

分析：

关系 R (A，Y)、S (Y，Z)

P(A) = R÷S      (经过除法运算得到一个新的关系P(A))

关系R在A上分量值a的象集 称作 seta

关系S在Y属性组上投影的集合 称作setY

若seta包含了 setY,  则 a 就是关系P中的元组分量

例如：

关系R和关系S拥有共同的属性Cno、R÷S得到的新关系中存在着“关系R包含但关系S不包含“”的属性，即Sno属性

=======================================================================================================