
背景
以前整理了两位数乘法的常用技巧和原理,可参考【数学 | 小学】乘法速算技巧大全,但分类较多,篇幅较长,阅读不易。
恰好看到小朋友的数学课本中开始教两位数乘法,于是重新整理了下。
在两位数乘法中,最重要也最容易被小朋友理解的应该是互补类的两位数乘法,有些原理,小学的小朋友可能难以理解,不过希望小朋友能强记。至于其他的两位数乘法,看情况吧,能记就记,也可留待以后慢慢再掌握。
原理
两位数的基本原理一定要弄懂,要掌握好,如果原理没弄懂,记住本文里的技巧也是无源之水无本之木。
最小的两位数是10,最大的两位数是99。
最小的两个两位数相乘,就是:
最大的两个两位数相乘,就是:
所以,两个两位数相乘,其结果不是三位数就是四位数。
小学三年级的小朋友,现在已经开始学乘法了。我们以为例,数学书上有如下类似的表格让我们填充:
什么意思呢?眼尖的小朋友可能已经发现了:
所以啊:
拆分出来的数字前后两两相乘,十位和十位相乘有一次,个位和个位相乘有一次,个位和十位相乘有两次:
依次将结果填入前面的表格,就是:
依次将这4个乘积相加,就是的乘积:
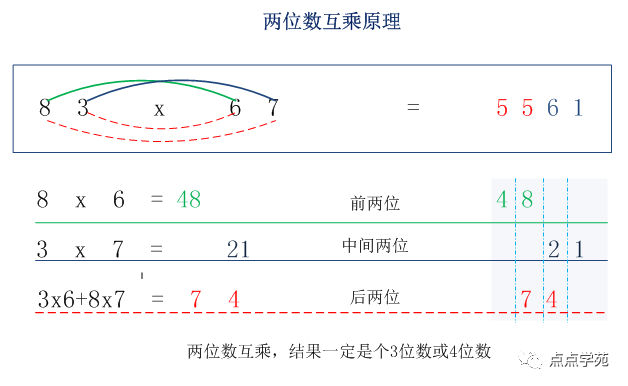
看到没有,百位数上其实是48,十位数上是56+18=74(百位进7),个位数上是21(十位进2)。
分解示意图如下所示:
互补类速算技巧
首先,我们介绍两类最重要最好记的两位数速算技巧,这两个一定要掌握。
这两个两位数有个特征:
- 十位数相同,个位数互补;
- 个位数相同,十位数互补;
互补是什么意思呢?就是两个数是“好朋友”,它们的和是10。譬如4和6互补,8和2互补,因为这些好朋友的和都是10。所以4是6的补数,6是4的补数。如果两数的和是100,我们也可认为其互补。
头相同,尾互补
"头同尾互补",这种类型估计是最广为人知的两位数速算法了。
譬如、,诸如此类,这种两位数乘法不用死算,一眼就可“拼”出答案。


尾相同,头互补
和“头同尾互补”类似,也存在“尾同头互补”的两位数速算法。
譬如,其乘积的前两位数等于两个十位数相乘加上个位数,其乘积的后两位数就是个位数相乘。

其实,对于乘积的前两位数,还有另外一种速算法。
大家注意到没有:
也就是说,可以用任一乘数减去其十位数的平方,得到的差就是乘积的前两位。很明显,使用小的乘数,计算量会小很多。
注意:
这种自个和自个相乘的数叫平方数,以后我们会学到。
头不同,尾互补
此类速算技巧也有公式,稍微难记了点,但我们可以将其转换为“头同尾互补”的类型来计算。
譬如,我们可以这样来计算:
其中就符合“头同尾互补”这种类型。
尾不同,头互补
同样,此类速算技巧也是有公式的,但为了减少记忆量,我们将其转换为“尾同头互补”的类型来计算。
譬如,我们可以这样来计算:
其中,就符合“尾同头互补”这种类型。
头同尾不同速算技巧
对于“头同尾不同”的乘法计算,如果速算规则记不住,可以将其转换为互补类型去计算,虽然减少记忆量,但代价就是增加了点计算量。
头是1,尾不同
头是1时,结果总是一个三位数。
譬如,计算过程如下:
- 先找出较大数18;
- 用18加上较小数的个位数,就是;
- 个位数乘积为;
- 22末尾补0后与32相加,乘积即。

如果上述规则不想记,如果个位数接近于互补数,我们也可以转换为尾互补的方式去计算。
譬如:
如果个位数离互补还比较远,转换成互补的方法去计算,得不偿失,计算量偏大。
譬如:
计算起来,后面是个两位数的加减法,就稍微有点麻烦,不如用公式直接。
头是2,尾不同
方法和头是1的一样,只是多了个乘法。
譬如我们来看:
- 先找出较大数28;
- 较大数和较小数个位相加,再乘以十位数2,就是;
- 个位数相乘,就是;
- 64末尾补0后再和32相加,就是。

同理,对于末位互补或接近互补的,也可转换为互补类去快速计算。
头是9,尾不同
十位数是9时,计算结果肯定都是个四位数。
譬如,计算方法如下:
- 先找出两个大数的补数,的补数是,的补数是;
- 较小数减去较大数的补数,就是,当然;
- 补数相乘,可以得到;
- 乘积的前两位就是,后两位就是,乘积就是。

当然,如果尾部互补或接近互补,也可以转换为互补类去计算,但牵涉到两位数的加减,估计没有这样算简洁。
下面,还提供另外一种速算方法,以为例:
- 用固定的 去加上个位数的和,就是;
- 补数的乘积为;
- 乘积的前两位就是,后两位就是35,乘积就是。

头是8,尾不同
以为例,计算方法如下:
- 分别求出两个乘数相对于的补数,譬如分别为和;
- 用任一个乘数减去另一个乘数的补数,譬如;
- 补数相乘,使用“头是1”的快速算法,;
- 末尾添两个,加上,就是乘积。

也有其他一种快速算法,譬如以为例:
- 用固定的 加上个位数和,就是;
- 后面的方法和前面一样,两个补数相乘,就是;
- 末尾添两个加上,乘积就是。

头是5,尾不同
以为例,计算方法如下:
- 先求出个位数和的一半,譬如,得到商和余数;
- 十位数相乘再和前面的商相加,就是;
- 个位数相乘就是;
- 如果前面的余数是,乘积就是,否则就再加上,乘积就是。

其他
头相同的万能速算法,不要求弄懂或者记住。
我们假设十位数是k,两个个位数分别是a和b,就是:
所以,当作乘积的前两位,当作乘积的后两位,拼成的数字再加上的10倍,就是最终的乘积。
尾同头不同速算技巧
对于“尾同头不同”的乘法计算,如果速算规则记不住,可以将其转换为互补类型去计算,虽然减少记忆量,但代价就是增加了点计算量。
头不同,尾是1
以为例,计算规则如下:
- 十位数乘积是,其中2是百位数;
- 十位数和为,其中1是百位数;
- 个位数乘积是1;
- 乘积就是。

头不同,尾是2
以为例,和“头是2,尾不同”类似,计算方法如下:
- 十位数相乘得到,注意2在百位数上;
- 十位数的和再乘以2,得到,这里的2也在百位数上;
- 个位数相乘,得到;
- 乘积就是,或者当作乘积的前两位,十位上的4和个位上的4拼接在一起就是后两位。

头不同,尾是9
以为例,和“头是9,尾不同”类似,计算方法如下:
- 十位数的乘积加上十位数的和,就是;
- 个位数乘积就是;
- 十位数的和是;
- 乘积就是

其实,,所以,还有下面这种算法:
- 将乘数都加上其补数1,将新数的头部相乘,就是;
- 新乘数的头相加,就是;
- 补数相乘,就是;
- 乘积就是。
这两种方法,都牵涉到三位整十数的减法,有点计算量。
头不同,尾是8
方法和前面介绍的都类似,只是稍微有点差异,以为例,计算方式如下:
- 头相乘后分别加上两个头,就是,其实也就是;
- 头相加和补数相乘,就是;
- 尾数积为;
- 乘积就是。

注意,这里也牵涉到三位整十数的减法,考验计算能力。
同样,也可以用补数的方法来计算:
- 前两位和后两位拼成;
- 减去;
- 最终的乘积就是。
头不同,尾是5
以为例,方法和“头是5,尾不同”类似,计算方式如下:
- 十位数相乘是;
- 十位数相加的一半为,其中
6是商,余数是1; - 如果余数是0,则乘积前两位就是,后两位就是,拼起来就是;如果余数是1,则再加上50,就是。

其他
尾数相同的万能速算法,不要求弄懂或者记住。
我们假设个位数是k,两个十位数分别是a和b,就是:
所以,当作乘积的后两位,当作乘积的前两位,拼成的数字再加上的10倍,就是最终的乘积。
例题训练
小朋友们,掌握得怎么样了,下面来练习练习吧,看看能快速计算的有多少:

【数学 | 中学】整除11之类的求余题的快速解答技巧
【数学 | 中学】第20届华罗庚金杯少年邀请赛初赛A试卷(初一组)试题解析
【数学 | 中学】第20届华罗庚金杯少年邀请赛初赛A试卷(初一组)试题解析
【数学 | 中学】由一道开方题展开的手工开方的探索
【数学 | 中学】2017年全国数学联赛初三A组试题解析
【数学 | 小学】第23届华罗庚金杯少年数学邀请赛初赛试卷
【数学 | 中学】第27届希望杯全国数学邀请赛初二第一试试题解析
【数学 | 高中】2019年高考数学部分试题解析
【数学 | 小学】2018百外小升初数学真题解析
更多数学类文章,请关注菜单栏目:
数学栏目
数学试题解析























 7076
7076

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








