高等数学上：函数的极限（重难点）

2019.03.26
参考资料：mooc西华大学高等数学课程

昨天学习了数列的极限，今天我们来讨论函数的极限
首先我们来讨论当 自变量趋近于无穷大 的时候，函数的极限
很明显，x->无穷，包含两种情况，x->正无穷和x->负无穷

1.x->正无穷时的定义其实可以参照数列的定义（很像）：

对于任意的e > 0，存在X > 0
使得所有的x > X的 |f(x) - A| < e。那么函数在x->正无穷时存在极限A

这里注意，与数列极限的定义唯一不同的地方就是，X不再一定要求是正整数了。原因很简单，数列中的定义域是所有自然数，而函数是一切的实数。
这个定义说通俗点就是，如果函数在正无穷上极限存在，那么从某一个位置X开始之后的所有x对应的f(x)到极限A的距离，肯定能无限小

2.x->负无穷时的定义（可以参考正无穷时的定义）

对于任意的e > 0，存在X > 0
使得所有的x < -X 的 |f(x) - A| < e。那么函数在x->负无穷时存在极限A

跟正无穷的极限定义类似，强调的是某一个位置之后的所有x对应的函数值与极限的距离可以无限小！

3。 在理解了上述极限的定义之后，那么x->无穷时的极限定义就出来了：

对于任意的e > 0，存在X > 0
使得所有的|x| > X 的 |f(x) - A| < e。那么函数在x->无穷时存在极限A

无穷时，就是相当于包括了正无穷和负无穷两种情况。
因此顺其自然的有一个定理：

x趋近于无穷大的时候极限为A	的充分必要条件是	x趋近于正无穷时的极限为A且x趋近于负无穷时的极限为A

如果说理解了定义，这个定理就是顺其自然的

下面看看x趋近于无穷时的几何解释，更直观：

---

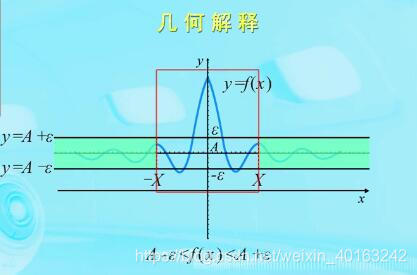
下面我们探讨函数极限的另一种情况
当自变量趋近于有限值时的函数的极限

可以看看上面这两个函数，我们讨论在x趋近于2的时候，函数的极限。
那么其实我们根据前面所学的极限知识，都可以自己推导一下这个的定义了。

对于任意的e > 0，都存在一个X > 0
使得Uo(x0, X)中的所有x对应的函数值f(x)满足一个|f(x) - A| <ｅ

这个定义是我自己仿照前面的思想推出来的，虽然和书上的有细微差别，但就是字母和表达方式的差别，意思完全一样，我觉得这个表达更直观。
根据前面的极限思想，那么x在x0处存在极限A，不就是说x在x0的某个去心邻域内，都有f(x)到A的距离比任意小都小吗？ 和前面的极限思想大同小异。

下面是几何解释：

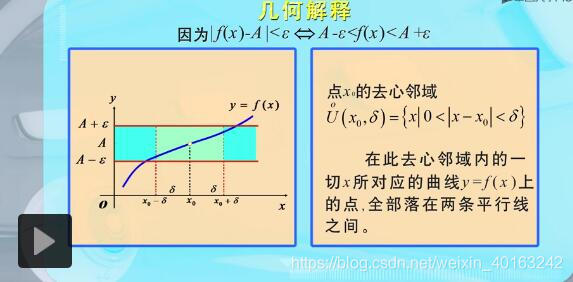
下面来几道例题：
1.证明函数y = x在x趋近于正无穷的时候，极限不存在
似乎感觉画图一下就出来了，这里我们采用定义严格证明。
用反证法证明！ 先假设极限存在

2.证明函数y = 1/ x在x->正无穷的时候极限值为0
过程类似

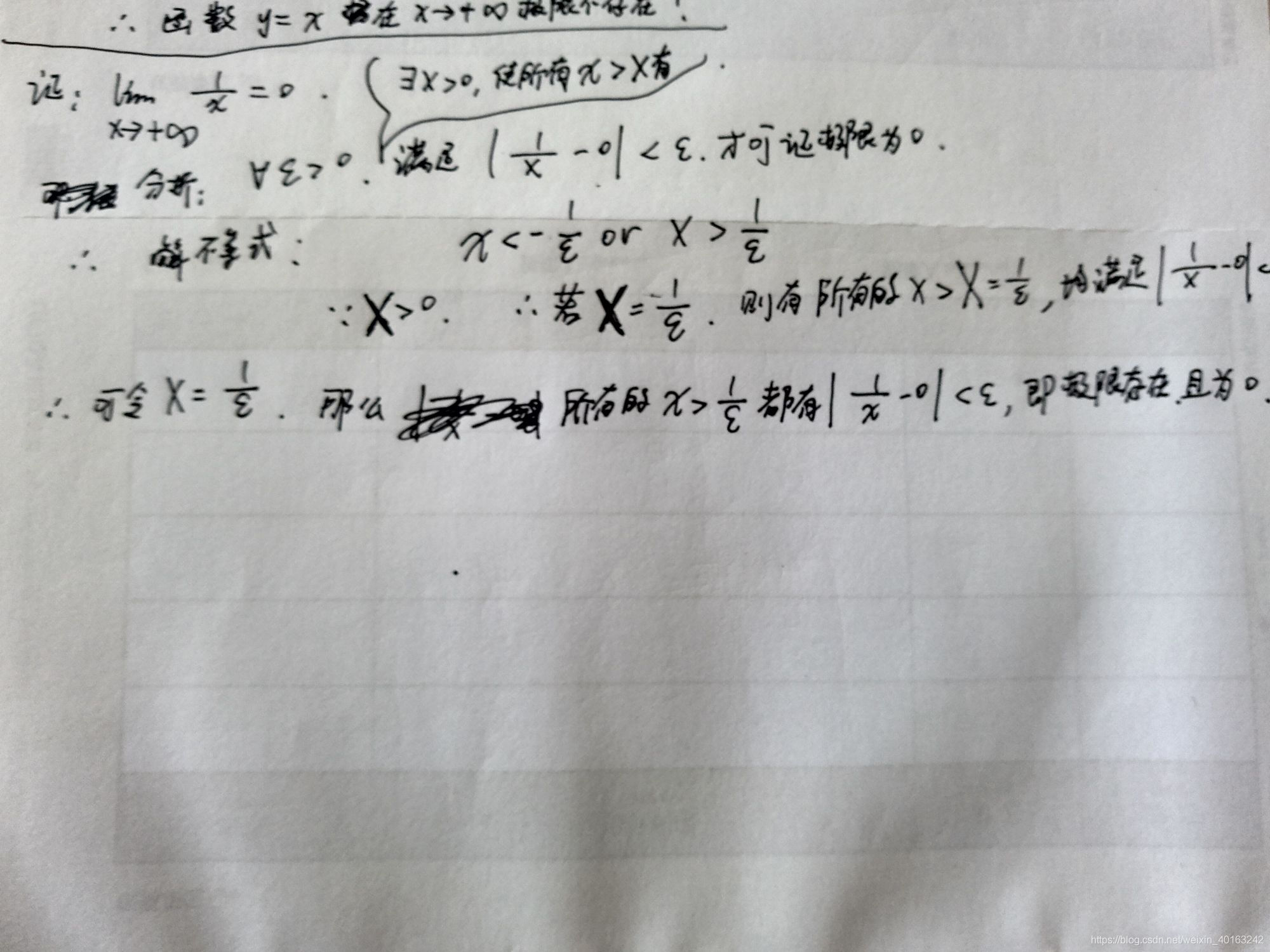
最后再谈谈和自变量趋近于有限值相关的，左右极限的概念。

x从左边趋近于x0，称为x0的左极限，记为x->x0-
同理也有右极限x0+

定理：函数在x趋近于x0时存在极限值A的充要条件为：x在x0处左右极限都存在
且都相等为A！
这个定理常用于判断函数在某个点极限是否存在。如果两边极限值不等，即不存在

其实有点像前面讲到的无穷大时的那个极限定理，无穷大时极限存在的充要条件是
正无穷和负无穷极限都存在且相等！

通过今天的学习，终于弄清楚了当初大一没有弄懂的函数极限的概念，记得当时这里学得一团糟，现在终于理顺了。