ALGLIB学习笔记（1）

最新推荐文章于 2025-03-22 01:08:29 发布

braveheartwm

最新推荐文章于 2025-03-22 01:08:29 发布

阅读量8.9k

点赞数 5

分类专栏：程序猿文章标签：数值算法

本文链接：https://blog.csdn.net/weixin_40198941/article/details/94393918

版权

程序猿专栏收录该内容

7 篇文章

订阅专栏

文章目录

ALGLIB简介
选择ALGLIB的理由
ALGLIB结构及相关概念
编译和引用ALGLIB
简单的一个求极值例子

ALGLIB简介

ALGLIB是一个跨平台数值分析和数据挖掘库，支持多种编程语言（C++，C#，Delphi，VB.NET，Python）和多种操作系统（windows,unix family)。
ALGLIB特性包括：

数据分析（分类，回归，统计）
优化和非线性求解器
插值和线性/非线性最小二乘拟合
线性代数（直接算法，EVD/SVD），直接和迭代线性求解器
快速傅里叶变换和许多其他算法

ALGLIB通常会提供两个版本：免费版本和商业版本

选择ALGLIB的理由

便携。几乎任何编译器都可以在几乎任何地方编译它。
使用方便。易于集成，附带大量文档。
高效。内部深度算法和低级优化。
受到领先公司的信赖。从核研究到航空航天。

ALGLIB结构及相关概念

文件结构

这里选择C++版本进行学习选择free C++版本
下载解压可以看到cpp文件夹，该文件包含了该库所有文件。
在这里插入图片描述
其cpp文件夹下文件结构如下：

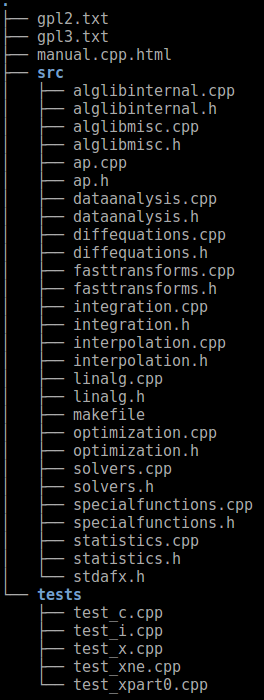
包

ALGLIB其计算核心是由C语言编写，但其提供的是C++接口。C库和C++包装器（wrapper)都是由ALGLIB项目中的代码生成工具自动生成的。在3.0版本之前，包含100多个单元，因此很难处理。自3.0以后所有的单元合并为11个包和2个支持单元：

alglibmisc.cpp - 很难被分类的算法
dataanalysis.cpp - 数据挖掘算法
diffequations.cpp - 微分方程求解器
fasttransforms.cpp - FFT以及相关算法
integration.cpp - 包含数值积分算法
interpolation.cpp - 包含插值算法
linalg.cpp - 线性代数算法
optimization.cpp - 优化算法
solvers.cpp - 线性和非线性求解器
specialfunctions.cpp - 特殊函数
statistics.cpp - 统计
alglibinternal.cpp - 其他包需要但不暴露给外面的内部函数
ap.cpp - 包含可公开访问的向量/矩阵类，最重要的和通用的函数以及其他“基本”功能

一个包依赖另一个包，但开发者尽量减小依赖数，每个包均依赖于ap.cpp,以及许多包依赖alglibinternal.cpp .

子包

每个包都是由多个源文件构成的，例如(ALGLIB3.0.0)linalg.cpp由14个.cpp文件和14个.c文件合并而来。这个文件提供了不同的功能，为了便于使用和阅读，相关的文件并未随着代码的合并而合并。

每个包包含了不同的子包，例如linalg.cpp包含trfac，svd，evd和其他子包。这些子包不存在独立的文件，命名空间或者其他的实体，它们只是一个大单元的子集，提供了截然不同的功能。它们有单独的文档部分，但是如果要使用svd子包，则必须包含linalg.h，而不是svd.h。也就是说，其子包只是为了阅读方便。

编译和引用ALGLIB

在一个项目中，使用ALGLIB库非常的简单明了，只需要将其中涉及到的文件加入到你自己的源文件中就可以，其编译器如果为GCC或者MSVC时，则不需要任何额外的设置。这里我们采用GCC，因此无需多余的设置。

简单的一个求极值例子

ALGLIB这里给出利用ALGLIB求解QP问题的例子，以简要了解其工作原理和流程：
该例子最小化函数
$F(x_0,x_1) = x_0^2 + x_1^2 -6x_0 - 4x_1$
其中：
$0.0 <= x_0,x_1 <= 2.5$
其正确解为： $x_0=2.5,x_1=2.0$

建立demo1文件夹，并在里面创建main.cpp文件，其文件内容如下：

#include "stdafx.h"
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include "optimization.h"

using namespace alglib;


int main(int argc, char **argv)
{
    //
    // This example demonstrates minimization of F(x0,x1) = x0^2 + x1^2 -6*x0 - 4*x1
    // subject to bound constraints 0<=x0<=2.5, 0<=x1<=2.5
    //
    // Exact solution is [x0,x1] = [2.5,2]
    //
    // We provide algorithm with starting point. With such small problem good starting
    // point is not really necessary, but with high-dimensional problem it can save us
    // a lot of time.
    //
    // Several QP solvers are tried: QuickQP, BLEIC, DENSE-AUL.
    //
    // IMPORTANT: this solver minimizes  following  function:
    //     f(x) = 0.5*x'*A*x + b'*x.
    // Note that quadratic term has 0.5 before it. So if you want to minimize
    // quadratic function, you should rewrite it in such way that quadratic term
    // is multiplied by 0.5 too.
    // For example, our function is f(x)=x0^2+x1^2+..., but we rewrite it as 
    //     f(x) = 0.5*(2*x0^2+2*x1^2) + ....
    // and pass diag(2,2) as quadratic term - NOT diag(1,1)!
    //
    real_2d_array a = "[[2,0],[0,2]]";
    real_1d_array b = "[-6,-4]";
    real_1d_array x0 = "[0,1]";
    real_1d_array s = "[1,1]";
    real_1d_array bndl = "[0.0,0.0]";
    real_1d_array bndu = "[2.5,2.5]";
    real_1d_array x;
    minqpstate state;
    minqpreport rep;

    // create solver, set quadratic/linear terms
    minqpcreate(2, state);
    minqpsetquadraticterm(state, a);
    minqpsetlinearterm(state, b);
    minqpsetstartingpoint(state, x0);
    minqpsetbc(state, bndl, bndu);

    // Set scale of the parameters.
    // It is strongly recommended that you set scale of your variables.
    // Knowing their scales is essential for evaluation of stopping criteria
    // and for preconditioning of the algorithm steps.
    // You can find more information on scaling at http://www.alglib.net/optimization/scaling.php
    //
    // NOTE: for convex problems you may try using minqpsetscaleautodiag()
    //       which automatically determines variable scales.
    minqpsetscale(state, s);

    //
    // Solve problem with QuickQP solver.
    //
    // This solver is intended for medium and large-scale problems with box
    // constraints (general linear constraints are not supported).
    //
    // Default stopping criteria are used, Newton phase is active.
    //
    minqpsetalgoquickqp(state, 0.0, 0.0, 0.0, 0, true);
    minqpoptimize(state);
    minqpresults(state, x, rep);
    printf("%d\n", int(rep.terminationtype)); // EXPECTED: 4
    printf("%s\n", x.tostring(2).c_str()); // EXPECTED: [2.5,2]

    //
    // Solve problem with BLEIC-based QP solver.
    //
    // This solver is intended for problems with moderate (up to 50) number
    // of general linear constraints and unlimited number of box constraints.
    //
    // Default stopping criteria are used.
    //
    minqpsetalgobleic(state, 0.0, 0.0, 0.0, 0);
    minqpoptimize(state);
    minqpresults(state, x, rep);
    printf("%s\n", x.tostring(2).c_str()); // EXPECTED: [2.5,2]

    //
    // Solve problem with DENSE-AUL solver.
    //
    // This solver is optimized for problems with up to several thousands of
    // variables and large amount of general linear constraints. Problems with
    // less than 50 general linear constraints can be efficiently solved with
    // BLEIC, problems with box-only constraints can be solved with QuickQP.
    // However, DENSE-AUL will work in any (including unconstrained) case.
    //
    // Default stopping criteria are used.
    //
    minqpsetalgodenseaul(state, 1.0e-9, 1.0e+4, 5);
    minqpoptimize(state);
    minqpresults(state, x, rep);
    printf("%s\n", x.tostring(2).c_str()); // EXPECTED: [2.5,2]
    return 0;
}