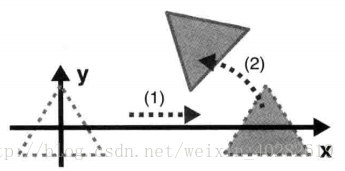
目标:实现三角形的 先旋转再平移
结果:
本节要使用一个专为本书编写的矩阵函数库。有了矩阵函数库,进行如“平移,然后旋转”这种复合的变换就很简单了。
矩阵变换库:cuon-matrix.js
在 OpenGL 中,我们无需手动指定变换矩阵的每个元素,因为 OpenGL 提供了一系列有用的函数来帮助我们穿件变换矩阵。比如,通过调用 glTranslate ()函数并传入在X、Y、Z轴上的平移的距离就可以创建一个平移矩阵。
遗憾的是,WebGL 没有提供类似的矩阵函数,如果想要使用他们,你就得自己编写,或者使用其他人已经编写好的。因为矩阵函数非常有用,所以书的作者专门编写了一个JS函数库 cuon-matrix.js。该函数允许你通过Open GL 中类似的方法创建变换矩阵。虽然这个库是专门为本书编写的,你也可以在自己的程序中使用它。
Matrix4 是矩阵库提供的新类型,顾名思义,Matrix4 对象表示一个 4x4 的矩阵。该对象内部使用类型化数组 Floated2Array 来存储矩阵的元素。
我们来利用 Matrix4 和其相关的方法来把 RotatedTriangles_Matrix 程序重写一遍,找找使用这个矩阵函数库的感觉。
示例程序
这个示例程序相比于第3章中的 RotatedTriangle_Matrix.js,唯一的改动发生在新步骤上:创建变换矩阵,并将变换矩阵传给顶点着色器。
在 RotatedTriangle_Matrix.js 中,我们是这样创键变换矩阵的:
var radian = Math.PI * ANGLE / 180.0; // Convert to radians
var cosB = Math.cos(radian), sinB = Math.sin(radian);
var xformMatrix = new Float32Array([
cosB, sinB, 0.0, 0.0,
-sinB, cosB, 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
0.0, 0.0, 0.0, 1.0
]);在本例中,你需要利用一个 Matrix 对象比调用其setRotate()方法计算出旋转矩阵来重写这部分:
var ANGLE = 90.0;
//为旋转矩阵创建 Matrix4 对象
var xformMatrix = new Matrix4();
//将 xformMatrix 设置为旋转矩阵
xformMatrix.setRotate(ANGLE, 0, 0, 1);
//将旋转矩阵传输给顶点着色器
var u_xformMatrix = gl.getUniformLocation(gl.program, 'u_xformMatrix');
if(u_xformMatrix < 0){
console.log("Failed to get the storage location of u_xformMatrix");
return;
}
gl.uniformMatrix4fv(u_xformMatrix, false, xformMatrix.elements);可见,创建变换矩阵然后传给 uniform 变量的基本步骤,在这两个示例程序中是相同的:使用 new 操作符新建一个 Matrix4 对象,就像我们使用 new 操作符创建一个 Array 对象或 Date 对象一样。我们新建了一个 Matrxi4对象 xformMatrix,并调用其 setRotate()方法把自身设为计算出的旋转矩阵。
setRotate()函数接受的参数是旋转角(角度制而非弧度制)和旋转轴(x, y, z)。旋转轴(x, y, z)表示旋转是绕着从原点(0, 0, 0)指向(x, y, z)的轴进行的。第3章说过,如果旋转角度值是正值,那么旋转就是逆时针方向的。本例中的旋转是绕Z轴进行的,所以旋转轴设为(0, 0, 1):
xformMatrix.setRotate(ANGLE, 0, 0, 1);类似的,如果是绕 X 轴旋转的,那么旋转轴的三个分量x = 1, y = 0, z = 0;如果是绕 Y 轴旋转的,则 x = 0, y = 1, z = 0。一旦你在 xformMatrix 变量中设置好了旋转矩阵,剩下的任务只是用相同的 gl.uniformMatrix4fv()方法将旋转矩阵传入顶点着色器。注意,你不能将 Matrix4 对象直接作为最后一个参数传入,因为该方法的最后一个参数必须是类型化数组。你应当使用 Matrix4 对象的 elements 属性访问存储矩阵元素的类型化数组:
gl.uniformMatrix4fv(u_xformMatrix, false, xformMatrix.elements);Matrix4 对象所支持的方法和属性如下表所示:

从上表中科建,Matrix4 对象有两种方法:一种方法的名称中含有前缀 set,另一种则不含。包含 set 前缀的方法会根据参数计算出变换矩阵,然后将变换矩阵写入到自身中;而不含 set 前缀的方法,会先根据参数计算出变换矩阵,然后将自身与刚刚计算得到的变换矩阵相乘,然后把最终得到的记过再写入到 Matrix4 对象中。
如上表所示, Matrix4 对象的方法十分强大且灵活。更重要的是,有了这些函数,进行变换就会变得轻而易举。比如,如果本例中你不希望对三金星进行旋转,而希望对它进行平移,你只需要重写一下内容:
xformMatrix.setTranslate(0.5, 0.5, 0.0);复合变换
现在,你对 Matrix4 对象应该有了基本的了解,下面就来看看如何利用 Matrix4 将两次变换组合起来,即进行一次平移,再进行一次旋转。
显然,示例中包含了以下两种变换:
- 将三角形沿着 X 轴平移一段距离。
- 在此基础上,旋转三角形。
讲解了这么多,我们可以先写下第1条中的坐标方程式。
然后对<平移后的坐标>进行旋转
当然你也可以分布计算这两个等式,但更好的方法是,将等式1代入到等式2中,把两个等式组合起来:
这里
等于
最后,我们可以在JS中计算<旋转矩阵>x<平移矩阵>,然后将得到的矩阵传入顶点着色器。像这样,我们就可以把多个变换复合起来了。一个模型可能经过了多次变换,将这些变换全部复合成一个等效的变换,就得到了 模型变换,或称 建模变换,相应地,模型变换的矩阵称为 模型矩阵。
再来复习一下矩阵的乘法:
如上所示,将两个 3x3 矩阵 A 与 B 相乘的结果如下:
上式是两个 3x3 矩阵相乘的结果,实际用到的模型矩阵是 4x4 的矩阵。然后要注意,矩阵相乘的次序很重要,A*B 的结果并不一定等于 B*A。
如你所料,cuon-matrix.js 中的 Matrix4 对象支持矩阵乘法。下面就来看一下如何使用 Matrix4 对象进行矩阵乘法,从而将多个变换复合起来,实现先平移,然后旋转。
RotatedTranslatedTriangle.js
//顶点着色器程序
var VSHADER_SOURCE =
'attribute vec4 a_Position;'+
'uniform mat4 u_ModelMatrix;'+
'void main(){'+
'gl_Position = u_ModelMatrix * a_Position;'+
'}';
//片元着色器程序
var FSHADER_SOURCE=
'void main(){'+
'gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);'+
'}';
function main() {
//获取canvas元素
var canvas = document.getElementById("webgl");
if(!canvas){
console.log("Failed to retrieve the <canvas> element");
return;
}
//获取WebGL绘图上下文
var gl = getWebGLContext(canvas);
if(!gl){
console.log("Failed to get the rendering context for WebGL");
return;
}
//初始化着色器
if(!initShaders(gl,VSHADER_SOURCE,FSHADER_SOURCE)){
console.log("Failed to initialize shaders.");
return;
}
//设置顶点位置
var n = initVertexBuffers(gl);
if (n < 0) {
console.log('Failed to set the positions of the vertices');
return;
}
//计算模型矩阵
var ANGLE = 60.0; //旋转角
var Tx = 0.5; //平移距离
//为旋转矩阵创建 Matrix4 对象
var modelMatrix = new Matrix4();
modelMatrix.setRotate(ANGLE, 0, 0, 1);
modelMatrix.translate(Tx, 0, 0);
//将旋转矩阵传输给顶点着色器
var u_ModelMatrix = gl.getUniformLocation(gl.program, 'u_ModelMatrix');
if(u_ModelMatrix < 0){
console.log("Failed to get the storage location of u_ModelMatrix");
return;
}
gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements);
//指定清空<canvas>颜色
gl.clearColor(0.0, 0.0, 0.0, 1.0);
//清空<canvas>
gl.clear(gl.COLOR_BUFFER_BIT);
//绘制三个点
gl.drawArrays(gl.TRIANGLES, 0, n);
}
function initVertexBuffers(gl) {
var vertices = new Float32Array([
0.0, 0.3, -0.3, -0.3, 0.3, -0.3
]);
var n=3; //点的个数
//创建缓冲区对象
var vertexBuffer = gl.createBuffer();
if(!vertexBuffer){
console.log("Failed to create thie buffer object");
return -1;
}
//将缓冲区对象保存到目标上
gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
//向缓存对象写入数据
gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);
var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
if(a_Position < 0){
console.log("Failed to get the storage location of a_Position");
return -1;
}
//将缓冲区对象分配给a_Postion变量
gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);
//连接a_Postion变量与分配给它的缓冲区对象
gl.enableVertexAttribArray(a_Position);
return n;
}最关键的两行,我们计算了<旋转矩阵>x<平移矩阵>:
modelMatrix.setRotate(ANGLE, 0, 0, 1);
modelMatrix.translate(Tx, 0, 0);我们首先调用了包含 set 前缀的方法 setRotate(),传入的参数用以计算旋转矩阵,并写入 mpdelMatrix。接下来,我们调用了不带 set 前缀的方法 translate(),意思就是,先计算出一个平移矩阵,然后用原先存储在 modelMatrix 变量中的矩阵乘以这个新计算平移矩阵,将得到的结果写回 modelMatrix中。由于在第一步之后,modelMatrix 已经包含了一个旋转矩阵,那么经过了这一步,modelMatrix中的矩阵就是<旋转矩阵>x<平移矩阵>了。
你可能回注意到,“先平移后旋转”的顺序与构造模型矩阵<旋转矩阵>x<平移矩阵>的顺序是相反的,这是因为变换矩阵最终要与三角形的三个顶点的原始坐标矢量相乘。
最后,我们把矩形矩阵传递给顶点着色器中的 u_ModelMatrix 变量,并如常将平移和旋转后的红色三角形。









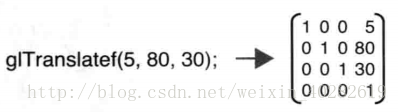

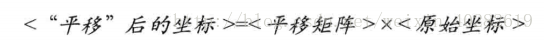




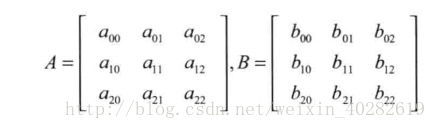
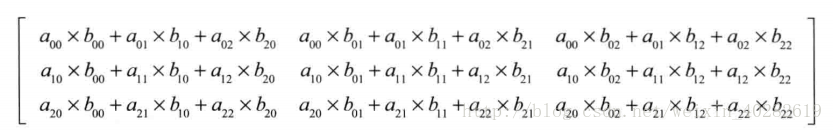















 304
304

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








