7.21晚上加赛 T2.七负我,做这题找到了性质发现需要求最大团,不会,爆搜,打假了,赛后改,对了,但时间复杂度大爆炸,看下发题解,有这么一句话: 于是学习了一下。
于是学习了一下。
updated on 7.24 增加了图片演示方便理解;
updated on 7.25 更新了 \(X\) 集合的作用和关键点优化的解释。
Bron-Kerbosch算法-求图的最大团,极大团
概念:
- 团:每个顶点都两两相连(又叫完全子图)
- 极大团:没有被包含在其他团中的团
- 最大团:顶点数最多的极大团
算法过程:
过程:
我们维护三个集合 \(R、P、X\),\(R\) 表示当前正在找的极大团里的点,\(P\) 表示有可能加入当前在找的极大团里的点,\(X\) 表示已经找到的极大团中的点(用来判重),进行以下过程:
-
初始化 \(R、 X\) 为空集,\(P\) 为包含所有点的集合;
-
将 \(P\) 中顶部元素 \(u\) 点取出,(设 \(Q(u)\) 为所有与 \(u\) 相邻的点)递归集合 \(R ∪{u},P ∩ {Q(u)},X ∩ {Q(u)}\);
- 在递归的过程中如果集合 \(P 和 X\) 都为空,则集合 \(R\) 中的点构成一个极大团。
- 在递归的过程中如果集合 \(P 和 X\) 都为空,则集合 \(R\) 中的点构成一个极大团。
-
将 \(u\) 点从集合 \(P\) 中删去,添加到集合 \(X\) 中;
-
不断重复 2~3 操作,直至 \(P\) 为空。
只看算法过程可能不好理解,那么下面是伪代码及分析。
伪代码(伪代码出处CSDN已改进):
void dfs(R, P, X){
if(P 和 X 均为空) 输出 R 集合为一个极大团
for 从 P 中选取一个点 a,与 a 相连的点集为 Q(a) {
dfs(R 并上 a,P 和 Q(a) 的交集,X 和 Q(a) 的交集)
从 P 中移除 a 点
把 a 点加入 X 集合
}
}
分析:
-
算法主要思路:很简单,我们每次枚举合法的点加入极大团中,合法即为保证该点加入团中,该团仍然是团,接着更新合法点集合(即可能属于在找的团的点集 \(P\) ),不断递归直到该团极大即可。
-
我们用 \(P\) 集合维护可能包含于目前所在找的极大团的点集,分析 \(P\) 集合是如何更进的:
\(R\) 是当前在找的极大团,由于 \(R\) 集合是每次任意从 \(P\) 中取一个点,我们知道团的定义为任意两个点都有边相连,所以若我把当前新选择的点 \(a\) 加入团中,那么 \(R\) 加入 \(a\) 之后,要想保证新 \(P\) 集合中的点可能包含于新 \(R\) 中团,那么需要满足 \(P\) 中的点都与 \(R\) 中任意一点相连。我们已经可以保证原 \(R\) (加入 \(a\) 之前)集合里所有点都与原 \(P\) 中的点相连,所以现在只需添加条件使得新 \(P\) 中的点与 \(a\) 点相连,于是 \(P∩{Q(a)}\) 是新 \(P\) 集合。 -
找到一个极大团时需要满足 \(P,X\) 集合都为空:
\(P\) 为空即再没有点可以加到 \(R\) 集合中,保证在找的团极大;\(X\) 为空保证之前没有找过此团,用来判重。 -
\(X\) 的作用:存每次计算到的极大团,避免在计算极大团数量的时候算重复,与优化时间复杂度无关。
图片演示:
如此图,蓝点为 \(P\) 集合中的点(可能属于当前在找的极大团中的点),橙点为 \(R\) 集合中的点(已经加入极大团中的点),灰色为啥也不是点。
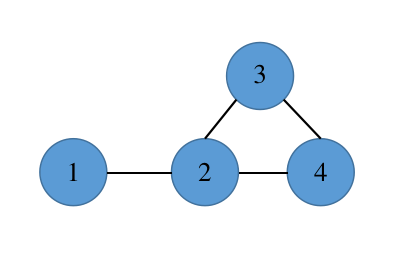
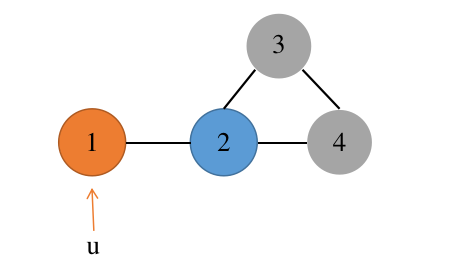
- 先取 \(1\) 号点作为 \(u\) 点加入 \(R\) (在找的团)中,此时我们递归集合 \((R\) ∪{1}, \(P ∩ Q(1)\), \(X ∩Q(u)\) ) ,\(Q(1)\)即与 \(1\) 相连的点——只有 \(2\) 号点,那么现在有 \(R=\){1}, \(P=\){2}, \(X=\) ∅,\(3,4\) 号点变为啥也不是点;
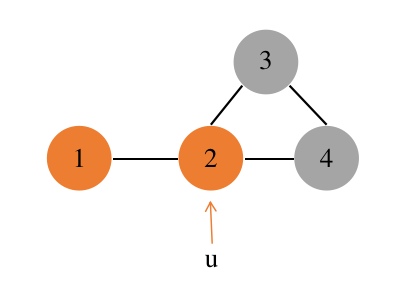
- 再从当前的 \(P\) 中取 2 号点加入 \(R\) 中,再次递归新集合(\(R\) ∪ {2}, \(P ∩ Q(2)\), \(X ∩ Q(2)\) )
- 在新的递归中我们发现 \(P, X\) 都为空,于是找到了一个极大团{1,2},回溯到第 1 步位置又开始了以 \(2\) 号点为 \(u\) 点的新递归;
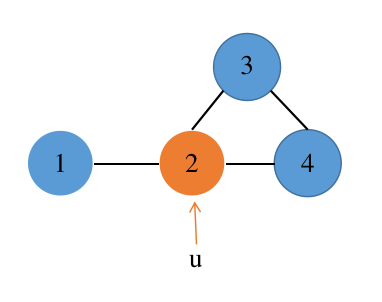
- 不在演示新递归,过程与之前一次一样,可以自己手模一下。
算法实现:
带详细注释code:
注:建议先看本篇博客的算法过程部分以方便看懂代码的注释int to[N][N], mnt; //to[i][j]用来判断 i 到 j 之间是否连边,mnt为最大团中点的个数
int had[N][N], may[N][N], vis[N][N]; //had,may,vis分别表示 当前在找的团中已有的点、可能加入当前在找的团中的点、已经搜过的点(分别对应算法过程的集合 R,P,X)
//had,may,vis的第一维i都表示处于搜索的第i层,第二维j表示相应的点的个数
//d表示当前搜索处于第几层,R、P、X分别表示had,may,vis在该层搜索中点的个数
void Bron_Kerbosch(int d, int R, int P, int X){
if(!P and !X){ mnt = max(mnt, R); return;} //找到一个极大团
for(int i=1; i<=P; i++){
int u = may[d][i]; //从 P 中取点
for(int j=1; j<=R; j++){
had[d+1][j] = had[d][j];
} had[d+1][R+1] = u; //即 R' = R + {u} 的操作
int newP = 0, newX = 0;
for(int j=1; j<=P; j++) // P' = P ∩ Q(u)
if(to[u][may[d][j]]) may[d+1][++newP] = may[d][j];
for(int j=1; j<=X; j++) // X' = X ∩ Q(u)
if(to[u][vis[d][j]]) vis[d+1][++newX] = vis[d][j];
Bron_Kerbosch(d+1, R+1, newP, newX); //递归搜索
may[d][i] = 0, vis[d][++X] = u; //将 u 点从 P 中删去,加入 X 中
}
}
到这里,就已经可以 A 掉那晚加赛的 T2.七负我 了。
AC 代码
#include<bits/stdc++.h>
#define mp make_pair
#define ll long long
using namespace std;
const int N = 50;
int n, m, x, hnt;
int to[N][N];
int had[N][N], may[N][N], vis[N][N];
void Bron_Kerbosch(int d, int R, int P, int X){
if(!P and !X){ hnt = max(hnt, R); return; }
for(int i=1; i<=P; i++){
int u = may[d][i];
for(int j=1; j<=R; j++){
had[d+1][j] = had[d][j];
} had[d+1][R+1] = u;
int newP = 0, newX = 0;
for(int j=1; j<=P; j++)
if(to[u][may[d][j]]) may[d+1][++newP] = may[d][j];
for(int j=1; j<=X; j++)
if(to[u][vis[d][j]]) vis[d+1][++newX] = vis[d][j];
Bron_Kerbosch(d+1, R+1, newP, newX);
may[d][i] = 0, vis[d][++X] = u;
}
}
signed main(){
// freopen("in.in", "r", stdin); freopen("out.out", "w", stdout);
scanf("%d%d%d", &n, &m, &x);
for(int i=1; i<=m; i++){
int a, b; scanf("%d%d", &a, &b);
to[a][b] = to[b][a] = 1;
}
int num = 0;
for(int i=1; i<=n; i++)
may[1][++num] = i;
Bron_Kerbosch(1, 0, num, 0);
double ans = x * 1.0 / hnt;
ans *= ans;
ans *= ((hnt - 1) * hnt / 2);
printf("%.6lf", ans);
return 0;
}
但是,这个算法还可以通过设定关键点(pivot vertex)\(v\) 进行优化。
主要优化原理:
图片来自oi-wiki:

简单解释一下:
意思就是说,在 \(P\) 集合取出一点 \(u\) 时,如果 \(P\) 中还有一点 \(v\) 与当前的 \(u\) 点相连,那么下一层递归中我们会取出一次 \(v\),而在本次递归中也会有一次取出 \(v\) 从而导致计算重复,所以我们进行关键点优化:
我们把从 \(P\) 中取出的第一个点记为 \(u\),如果本层递归中取到与 \(u\) 相连的点时,不进行下一层递归直接 continue 即可。
优化代码(纯享版):
int to[N][N], hnt;
int had[N][N], may[N][N], vis[N][N];
void Bron_kerbosch(int d, int R, int P, int X){
if(!P and !X) { hnt = max(hnt, R); return;}
int u = may[d][1];
for(int i=1; i<=P; i++){
int v = may[d][i];
if(to[u][v]) continue;
for(int j=1; j<=R; j++){
had[d+1][j] = had[d][j];
} had[d+1][R+1] = v;
int newP = 0, newX = 0;
for(int j=1; j<=P; j++)
if(to[v][may[d][j]]) may[d+1][++newP] = may[d][j];
for(int j=1; j<=X; j++)
if(to[v][vis[d][j]]) vis[d+1][++newX] = vis[d][j];
Bron_kerbosch(d+1, R+1, newP, newX);
may[d][i] = 0, vis[d][++X] = v;
}
}























 1212
1212

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








