一文让你读懂决策树算法

                                       决策树算法简介

决策树算法属于监督学习算法族。与其他监督学习算法不同，决策树算法也可用于解决回归和分类问题。

使用决策树的一般动机是创建一个训练模型，该模型可用于通过学习从先前数据（训练数据）推断的决策规则来预测目标变量的类或值。

与其他分类算法相比，决策树算法的理解水平非常简单。决策树算法试图通过使用树表示来解决问题。树的每个内部节点对应于属性，并且每个叶节点对应于类标签。

决策树算法伪码

1. 将数据集的最佳属性放在树的根部。
2. 将训练集拆分为子集。子集应该以这样的方式进行，即每个子集包含具有相同属性值的数据。
3. 对每个子集重复步骤1和步骤2，直到在树的所有分支中找到叶节点。

在决策树中，为了预测记录的类标签，我们从树的根开始。我们将根属性的值与记录的属性进行比较。在比较的基础上，我们遵循与该值对应的分支并跳转到下一个节点。

我们继续将记录的属性值与树的其他内部节点进行比较，直到我们到达具有预测类值的叶节点。我们知道如何使用建模的决策树来预测目标类或值。现在让我们了解如何创建决策树模型。

创建决策树时的假设

以下是我们在使用决策树时所做的一些假设：

• 一开始，整个训练集被视为根。
• 特征值优选是分类的。如果值是连续的，则在构建模型之前将它们离散化。
• 记录 基于属性值递归分布。
• 将属性作为树的根或内部节点放置的顺序是通过使用一些统计方法完成的。

 

决策树遵循产品总和（SOP）表示。对于上面的图片，你可以看到我们如何能够预测可 我们接受新的工作机会？每天使用电脑？ 从遍历根节点到叶节点。

这是产品代表的总和。产品总和（SOP）也称为析取范式。对于类，从树的根到具有相同类的叶节点的每个分支是值的连接（乘积），在该类中结束的不同分支形成分离（总和）。

决策树实现的主要挑战是确定我们需要考虑哪些属性作为根节点和每个级别。处理这个是知道属性选择。我们有不同的属性选择度量来识别可以被视为每个级别的根音的属性。

流行的属性选择措施：

• 信息增益
• 基尼指数

属性选择

如果数据集由“n”属性组成，那么决定将哪个属性放置在树的根或不同级别作为内部节点是一个复杂的步骤。通过随机选择任何节点作为根不能解决问题。如果我们遵循随机方法，它可能会给我们带来不良结果且准确度低。

为了解决这个属性选择问题，研究人员工作并设计了一些解决方案。他们建议使用一些  标准，如信息增益，基尼指数等。这些标准将计算每个属性的值。对值进行排序，并按照顺序将属性放置在树中，即，具有高值的属性（在信息增益的情况下）放置在根处。

在使用信息Gain作为标准时，我们假设属性是分类的，对于gini索引，假设属性是连续的。

信息增益

通过使用信息增益作为标准，我们尝试估计每个属性包含的信息。我们将使用从信息理论中扣除的一些点。
为了测量随机变量X的随机性或不确定性，由熵定义。

对于只有两个类，正类和负类的二进制分类问题。

• 如果所有示例都是正数或全部都是负数，那么熵将为零，即低。
• 如果一半的记录是正类，一半是负类，那么熵就是一个，即高。

 

通过计算每个属性的熵测量，我们可以计算他们的信息增益。信息增益计算由于对属性进行排序而导致的熵的预期减少。可以计算信息增益。

为了清楚地了解计算信息增益和熵，我们将尝试在样本数据上实现它。

示例：使用“信息增益”作为标准构建决策树

我们将使用此数据样本。让我们尝试使用信息增益作为标准。在这里，我们有5列，其中4列具有连续数据，第5列包含类标签。

A，B，C，D属性可以被视为预测变量，E列类标签可以被视为目标变量。为了从这些数据构建决策树，我们必须将连续数据转换为分类数据。

我们选择了一些随机值来对每个属性进行分类：

一个	乙	C	d
> = 5	> = 3.0	> = 4.2	> = 1.4
<5	<3.0	<4.2	<1.4

计算每个属性的信息增益有两个步骤：

1. 计算Target的熵。
2. 需要计算每个属性A，B，C，D的熵。使用信息增益公式，我们将从目标的熵中减去这个熵。结果是信息增益。

Target的熵：我们有8个负数类记录和8个正数类记录。因此，我们可以直接估计目标的熵为1。

变量E.
正	负
8	8

使用公式计算熵：

E（8,8）= -1 *（（p（+ ve）* log（p（+ ve））+（p（-ve）* log（p（-ve）））
= -1 *（（8 / 16）* log 2（8/16））+（8/16）* log 2（8/16））
= 1

Var A的信息增益

对于16个中的12个记录，Var A具有值> = 5，具有值<5值的4个记录。

• 对于Var A> = 5＆class == positive：5/12
• 对于Var A> = 5＆class == negative：7/12
  • 熵（5,7）= -1 *（（5/12）* log2（5/12）+（7/12）* log2（7/12））= 0.9799
• 对于Var A <5＆class == positive：3/4
• 对于Var A <5＆class == negative：1/4
  • 熵（3,1）= -1 *（（3/4）* log2（3/4）+（1/4）* log2（1/4））= 0.81128

熵（目标，A）= P（> = 5）* E（5,7）+ P（<5）* E（3,1）
=（12/16）* 0.9799 +（4/16）* 0.81128 = 0.937745

Var B的信息增益

Var B对于16个中的12个记录具有值> = 3，并且具有值<5值的4个记录。

• 对于Var B> = 3＆class == positive：8/12
• 对于Var B> = 3＆class == negative：4/12
  • 熵（8,4）= -1 *（（8/12）* log2（8/12）+（4/12）* log2（4/12））= 0.39054
• 对于VarB <3＆class == positive：0/4
• 对于Var B <3＆class == negative：4/4
  • 熵（0,4）= -1 *（（0/4）* log2（0/4）+（4/4）* log2（4/4））= 0

熵（目标，B）= P（> = 3）* E（8,4）+ P（<3）* E（0,4）
=（12/16）* 0.39054 +（4/16）* 0 = 0.292905

Var C的信息增益

对于16个中的6个记录，Var C具有值> = 4.2，具有值<4.2值的10个记录。

• 对于Var C> = 4.2＆class == positive：0/6
• 对于Var C> = 4.2＆class == negative：6/6
  • 熵（0,6）= 0
• 对于VarC <4.2＆class == positive：8/10
• 对于Var C <4.2＆class == negative：2/10
  • 熵（8,2）= 0.72193

熵（目标，C）= P（> = 4.2）* E（0,6）+ P（<4.2）* E（8,2）
=（6/16）* 0 +（10/16）* 0.72193 = 0.4512

Var D的信息增益

Var D对于16个中的5个记录具有值> = 1.4，并且具有值<5值的11个记录。

• 对于Var D> = 1.4＆class == positive：0/5
• 对于Var D> = 1.4＆class == negative：5/5
  • 熵（0,5）= 0
• 对于Var D <1.4＆class == positive：8/11
• 对于Var D <14＆class == negative：3/11
  • 熵（8,3）= -1 *（（8/11）* log2（8/11）+（3/11）* log2（3/11））= 0.84532

熵（目标，D）= P（> = 1.4）* E（0,5）+ P（<1.4）* E（8,3）
= 5/16 * 0 +（11/16）* 0.84532 = 0.5811575

目标 正 负 一个 > = 5.0 五 7 <5 3 1 信息增益A = 0.062255	目标 正 负 乙 > = 3.0 8 4 <3.0 0 4 信息增益B = 0.7070795
目标 正 负 C > = 4.2 0 6 <4.2 8 2 信息增益C = 0.5488	目标 正 负 d > = 1.4 0 五 <1.4 8 3 信息增益D = 0.41189

从上面的信息增益计算中，我们可以构建决策树。我们应该根据它们的值将属性放在树上。

具有比其他值更好的值的属性应该以root身份定位，并且具有熵0的分支应该被转换为叶节点。熵大于0的分支需要进一步分裂。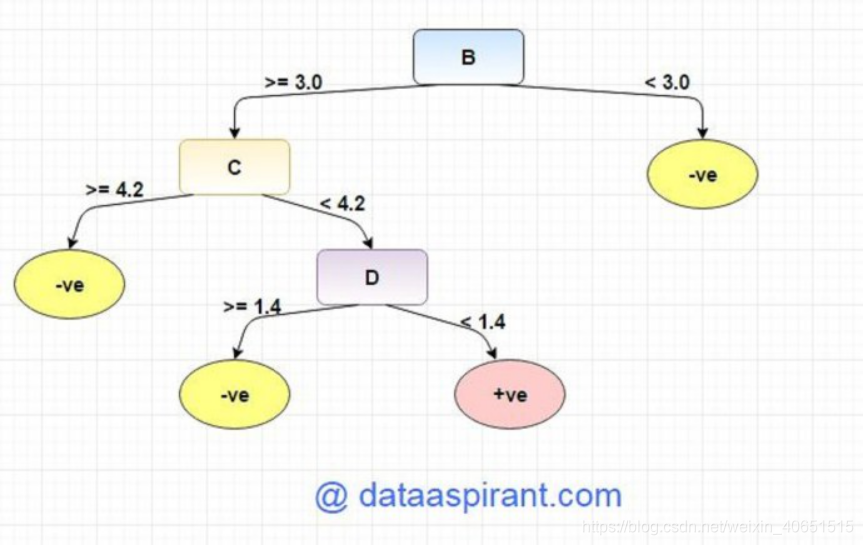

基尼指数

基尼指数是衡量随机选择的元素被错误识别的频率的指标。这意味着应该首选具有较低gini索引的属性。

示例：使用“gini index”作为标准构造决策树

我们将使用与信息获取示例相同的数据样本。让我们尝试使用基尼指数作为标准。在这里，我们有5列，其中4列具有连续数据，第5列包含类标签。

A，B，C，D属性可以被视为预测变量，E列类标签可以被视为目标变量。为了从这些数据构建决策树，我们必须将连续数据转换为分类数据。

我们选择了一些随机值来对每个属性进行分类：

一个	乙	C	d
> = 5	> = 3.0	> = 4.2	> = 1.4
<5	<3.0	<4.2	<1.4

Var A的基尼指数

对于16个中的12个记录，Var A具有值> = 5，具有值<5值的4个记录。

• 对于Var A> = 5＆class == positive：5/12
• 对于Var A> = 5＆class == negative：7/12
  • 基尼（5,7）= 1-（（5/12）2 +（7/12）2）= 0.4860
• 对于Var A <5＆class == positive：3/4
• 对于Var A <5＆class == negative：1/4
  • 基尼（3,1）= 1-（（3/4）2 +（1/4）2）= 0.375

通过增加权重并将每个基尼指数相加：

Var B的基尼指数

Var B对于16个中的12个记录具有值> = 3，并且具有值<5值的4个记录。

• 对于Var B> = 3＆class == positive：8/12
• 对于Var B> = 3＆class == negative：4/12
  • 基尼（8,4）= 1-（（8/12）2 +（4/12）2）= 0.446
• 对于Var B <3＆class == positive：0/4
• 对于Var B <3＆class == negative：4/4
  • gin（0,4）= 1-（（0/4）2 +（4/4）2）= 0

Var C的基尼指数

对于16个中的6个记录，Var C具有值> = 4.2，具有值<4.2值的10个记录。

• 对于Var C> = 4.2＆class == positive：0/6
• 对于Var C> = 4.2＆class == negative：6/6
  • gini（0,6）= 1-（（0/8）2 +（6/6）2）= 0
• 对于Var C <4.2＆class == positive：8/10
• 对于Var C <4.2＆class == negative：2/10
  • gin（8,2）= 1-（（8/10）2 +（2/10）2）= 0.32

Var D的基尼系数

Var D对于16个中的5个记录具有值> = 1.4，并且具有值<1.4值的11个记录。

• 对于Var D> = 1.4＆class == positive：0/5
• 对于Var D> = 1.4＆class == negative：5/5
  • gini（0,5）= 1-（（0/5）2 +（5/5）2）= 0
• 对于Var D <1.4＆class == positive：8/11
• 对于Var D <1.4＆class == negative：3/11
  • gin（8,3）= 1-（（8/11）2 +（3/11）2）= 0.397

wTarget 正 负 一个 > = 5.0 五 7 <5 3 1 Ginin指数A = 0.45825	目标 正 负 乙 > = 3.0 8 4 <3.0 0 4 基尼指数B = 0.3345
目标 正 负 C > = 4.2 0 6 <4.2 8 2 基尼指数C = 0.2	目标 正 负 d > = 1.4 0 五 <1.4 8 3 基尼指数D = 0.273

过度拟合

在构建决策树模型时，过度拟合是一个实际问题。该模型存在过度拟合的问题，当算法继续越来越深入以减少训练集错误时会考虑过度拟合，但结果会导致测试集错误增加，即我们模型的预测精度下降。它通常发生在由于异常值和数据不规则而构建许多分支时。

我们可以用来避免过度拟合的两种方法是：

• 预修剪
• 后修剪

预修剪

在预修剪中，它会提前停止树木结构。如果节点的良好度量低于阈值，则优选不分割节点。但是很难选择合适的停止点。

后修剪

在后期修剪中，它在树中越来越深，以构建完整的树。如果树显示过度拟合问题，则修剪作为修剪后步骤完成。我们使用交叉验证数据来检查修剪的效果。使用交叉验证数据，它测试扩展节点是否会改进。

如果它显示出改进，那么我们可以继续扩展该节点。但是如果它显示精度降低，则不应该扩展，即节点应该转换为叶节点。

决策树算法的优点和缺点

好处：

1. 决策树很容易解释。它产生一系列规则。
2. 它遵循人类在做出决策时通常遵循的相同方法。
3. 通过其可视化可以简化对复杂决策树模型的解释。即使是一个天真的人也能理解逻辑。
4. 要调整的超参数的数量几乎为空。

缺点：

1. 决策树中过度拟合的可能性很高。
2. 通常，与其他机器学习算法相比，它给数据集提供了低预测精度。
3. 具有分类变量的决策树中的信息增益给出具有更大数量的属性的偏差响应。类别。
4. 当有许多类标签时，计算会变得复杂。