Strassen：一种高效的矩阵相乘算法

Q1：如何提高矩阵相乘效率？

矩阵乘法是种极其耗时的运算。
以C = A • B为例，其中A和B都是 n x n 的方阵。根据矩阵乘法的定义，计算过程如下：

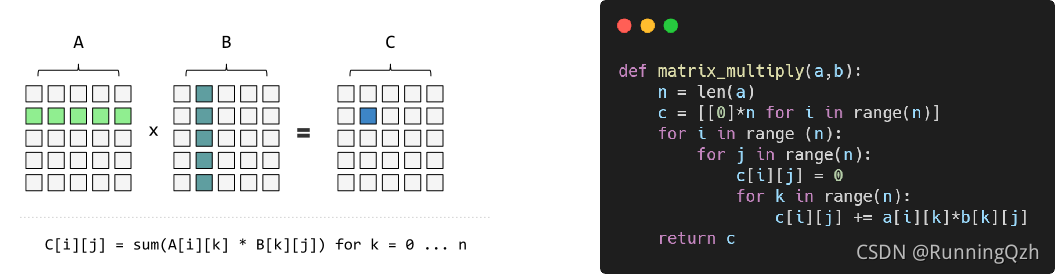
A1: 简单分治法

前提：假定A,B都是n等于2的次幂的方阵

基本思路：计算C=A*B时，将C,A,B矩阵进行分块操作，对每个分块的矩阵进行乘法运
算，运算完毕后重新对得到的C11,C12,C21,C22进行组合操作。

确定递归终止条件：当分块矩阵得到的阶数为1 时，得到的C即是A和B中两个元素的乘积。

每个公式需要计算两次矩阵乘法和一次矩阵加法，使用T(n)表示 n x n 矩阵乘法的时间复杂度，那么我们可以根据上面的分解得到一个递推公式。

T(n) = 8T(n/2) + Θ(n²)

其中，8T(n/2)表示8次矩阵乘法，而且相乘的矩阵规模降到了n/2。Θ(n²)表示4次矩阵加法的时间复杂度以及合并C矩阵的时间复杂度。

要想计算出T(n)并不复杂，可以采用画递归树的方式计算，或采用“主方法”直接计算。
结果是:

T(n) = Θ(n³)

可见，简单的分治策略并没有起到加速运算的效果。

简单分治策略为什么无法提高速度？

因为分解后的问题包含了8次矩阵相乘和4次矩阵相加，就是这8次矩阵相乘导致了速度不能提升。

于是我们想到能不能减少矩阵相乘的次数，取而代之的是矩阵相加的次数增加？
Strassen正是利用了这一点。

A2: Strassen

Strassen计算量是7个矩阵乘法和18个矩阵加法。虽然矩阵加法增加了好几倍，而矩阵乘法只减小了1个，但在数量级面前，18个加法仍然渐进快于1个乘法。

使用递归树或主方法可以计算出结果：T(n) = Θ(nlg7) ≈ Θ(n2.81)

代码：

output：

Q2：如何计算任意偶数阶矩阵相乘？

对于任意偶数n，总有n=m*(2^k)
将矩阵分成m*m个2^k阶矩阵。
举例：6X6矩阵相乘，可分为9个2x2矩阵，大矩阵用传统算法，小矩阵用Strassen。

Q3：对于任意正整数n，如何求n阶矩阵相乘？

将不是2的次幂的矩阵扩展成2的次幂的矩阵，在多出的行和列上添上0元素，在计算结果重新组合成c后，对c矩阵多出的行和列上的0元素舍去。

验证：

因此在原先的基础上增加了矩阵的拓展和缩略函数。
在主函数中，首先对输入矩阵A,B的阶数进行判断，如果是2的次幂则不用进行任何操作，直接用普通的Strassen算法，如果不是2的次幂，先对A,B进行矩阵拓展，在计算得到的结果后进行矩阵缩略。

over~