分析:状态值D[i][j]表示,将word1的前i个字符转化为word2的前j个字符需要的最少步骤数
本题是典型的适合使用动态规划的题目。在斯坦福的公开课(中文,英文)上,有对这个问题的详细说明,所以接下来就继续使用斯坦福公开课的例子了。
如果要计算单词"INTENTION"和单词"EXECUTION"之间的编辑距离,那么该怎么计算呢?
首先,把这个问题简单化。把上面两个单词简化为长度为1的两个单词I和E。
如果要“I”变化为"E",可以把"I"替换为"E"
如果要“I”变化为空串" ",可以把"I"删除,从而形成""
如果要空串“ ”变化为"E",可以把"E"插入,从而形成E
上面三种变化分别表示替换,删除,插入这三种基本操作。
接下来,定义一个表达式D(i,j)。它表示从第1个字单词的第0位至第i位形成的子串和第2个单词的第0位至第j位形成的子串的编辑距离。
显然,可以计算出动态规划的初始表达式,如下:
D(i,0) = i
D(0,j) = j
然后,考虑动态规划的状态转移方程式,如下:
D(i-1, j) + 1
D(i,j)=min ( D(i, j-1) + 1 )
D(i-1, j-1) +2( if X(i) != Y(j) ) ; D(i-1,j-1) ( if X(i) == Y(j) )
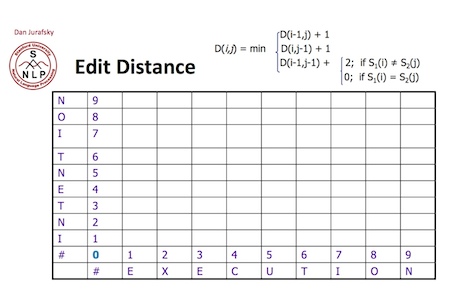
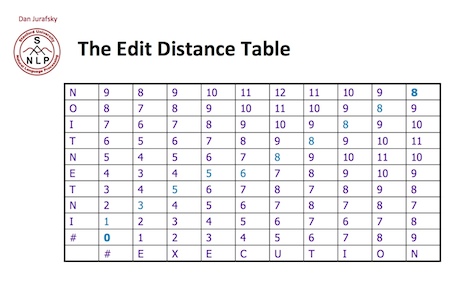
上面的状态转移方程的含义是,D(i,j)的值,要么是D(i-1, j)的操作完成之后删除一个字符(第1个单词的第i个字符),要么是D(i, j-1)的操作完成之后增加一个字符(第2个单词的第j个字符),要么是D(i-1, j-1)的操作完成自后替换一个字符(如果第1个单词的第i个字符和第2个单词的第j个字符不等),或者是D(i-1, j-1)的操作完成自后什么也不做(如果第1个单词的第i个字符和第2个单词的第j个字符相等)。其中,课件定义删除,插入,替换的操作步数分别为一步,一步,两步。lintcode测试时写的是一步
以第一个单词"INTENTION"和第二个单词"EXECUTION"为例,看下面的图
接下来,代码实现。注意在leetcode中,把插入,删除,替换全部视为一步操作。
代码:
class Solution {
public:
/**
* @param word1: A string
* @param word2: A string
* @return: The minimum number of steps.
*/
int minDistance(string &word1, string &word2) {
// write your code here
int len1=word1.size();
int len2=word2.size();
vector<vector<int>> dis_matrix(len1+1,vector<int>(len2+1,0));
for(int j=0;j<=len2;j++)
dis_matrix[0][j]=j;
for(int i=0;i<=len1;i++)
dis_matrix[i][0]=i;
for(int i=1;i<=len1;i++){
for(int j=1;j<=len2;j++){
int tmp_step;
if( word1[i-1]==word2[j-1])//注意这里下标容易写错。一开始写成了if(word[i]==word2[j])
tmp_step=0+dis_matrix[i-1][j-1];
else
tmp_step=1+dis_matrix[i-1][j-1];
int tmp_step2=min((dis_matrix[i-1][j]+1),(dis_matrix[i][j-1]+1));
dis_matrix[i][j]=min(tmp_step2,tmp_step);
}
}
return dis_matrix[len1][len2];
}
};





















 2971
2971











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








