转载:https://blog.csdn.net/zhangxz259/article/details/81627341
本文是从最基础的知识开始讲解,力求用最通俗易懂的文字将问题将的通俗易懂,大神勿喷,多多指教啊,虽然说是从零学习FFT,但是基本的数学知识还是要有的,sin,cos,等。
FFT(快速傅里叶变换)其本质就是DFT,只不过可以快速的计算出DFT结果,要弄懂FFT,必须先弄懂DFT,DFT(DiscreteFourier Transform) 离散傅里叶变换的缩写,咱们先来详细讨论DFT,因为DFT懂了之后,FFT就容易的多了
DFT(FFT)的作用:可以将信号从时域变换到频域,而且时域和频域都是离散的,通俗的说,可以求出一个信号由哪些正弦波叠加而成,求出的结果就是这些正弦波的幅度和相位,我们音乐播放器上面显示的就是音乐fft之后不同频率正弦波的幅度,就像下面这张图片:

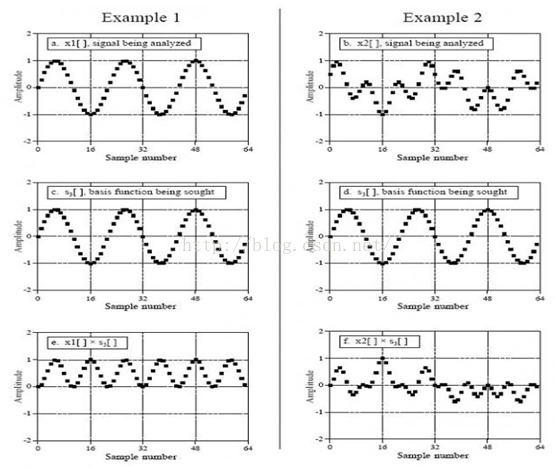
那么为什么可以求出正弦波的幅度呢,这里就要说一下信号的相关性了,我们也可以利用信号的相关性检测信号波中是否含有某个频率的信号波:把一个待检测信号波乘以另一个信号波,个新的信号波,再把这个新的信号波所有的点进行相加,从相加的结果就可以判断出这两个信号的相似程度,比如下图:
上图中a,b图是待检测信号,c,d是3个周期的正弦信号,很显然a图含有正弦波,e=a*c,将e图的各点相加,很显然值是正的,这就说明a图含频率为3的正弦波,f=b*d,显然将f图中各点相加结果约等于0了,说明b图不含有周期为3的正弦波,这就是dft的原理,也就是离散傅里叶变换的原理,其实就是这么简单,只不过dft将待检测信号和很多不同频率的正弦波和余弦波相乘,也就是进行了信号相关性检测,从而可以计算出信号中含有的正弦波的幅度,若含有此频率的正弦波,那么幅值不为0,若不含有此正弦波,那么幅值为0,那么幅值是如何计算出来的呢,幅值就是上面e图和f图各点之和(若是连续信号的话就是两信号乘积求积分了,。。额,不说积分,抽象了)
下面来看个具体的例子:
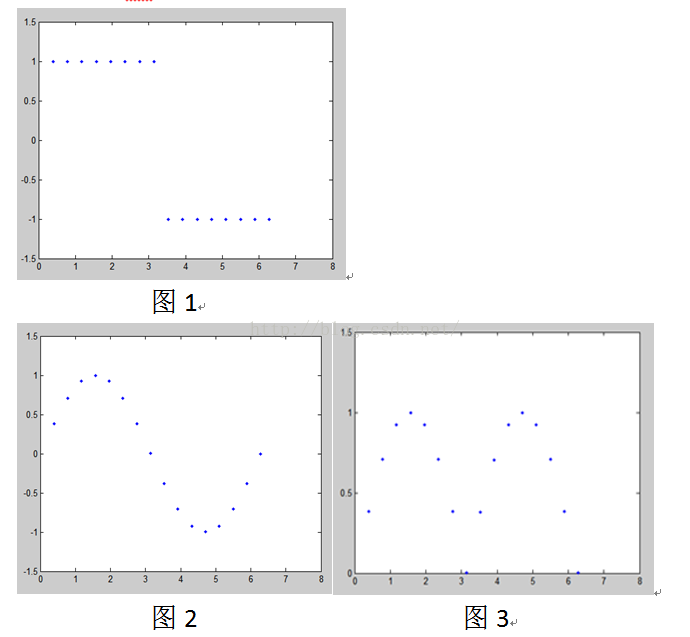
上面图一即为待检测信号,也就是将进行DFT变换的信号,将它分成16个离散的点,图2是一个频率为1的正弦波,也分成16个点,将对应的点相乘,得到图3,再将图3的各个点的幅值相加,结果为10.06,也就是说图1中的图像含有图2的正弦波,此时用到的dft点数就为16,10/(N/2)=10/8=1.25,含有的频率为1的正弦波的幅度就是1.25,以此类推,若要求是否含有频率为2的正弦波,将图1和频率为2的正弦波相乘再求和,。。。。
至于为什么要除以N/2,数字信号处理里面有讲,我就不多说了
接下来就是dft的实现了:
DFT的公式:
其中X(k)表示DFT变换后的数据,x(n)为采样的模拟信号,公式中的x(n)可以为复信号,实际当中x(n)都是实信号,即虚部为0,此时公式可以展开为:
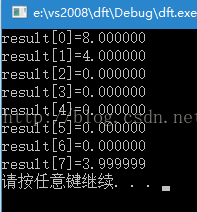
从这个公式可以看出,变换后的数据就是原信号对cos和sin的相关操作,即进行相乘求和(连续信号即为积分),为什么我要将n\N写在2k*pi后面呢?因为我觉得在对cos和sin进行相关操作时,k代表和频率为多少的正弦相关,而n和N则是在一个正弦周期内采样N个点,采样间隔为2*pi\N,,n用来步进,一次步进2*pi\N,最后进行累加求和,就得出了X(k),《实用数字信号处理》这本书的DFT章节详细的解释了此公式,并且还进行了举例,看了以后明白了不少,另外,DFT之后的数据是对称的,具体原因还是在那本书上面有,在FFT的章节。比如做8点DFT,采样信号为x(n),DFT之后的数据为X(k),那么X(0)为直流信号,X(1), X(2), X(3), X(5), X(6), X(7),关于X(4)对称,即X(1)=X(7), X(2)=X(6),X(3)=X(5),如下图,是对1+sin(2*PI)进行DFT变换,具体的幅值先不关心,只要知道它是对称的就行了。
接下来就是对公式写程序了,先将公式展开:
在计算机中可以这样展开:
里面有个j,不用管它,我们用两个数组,一个保存sin相关,一个保存cos相关,由于cos为实部,sin为虚部,可以定义以下两个数组:
float real[N];//用来保存cos相关。
float imag[N];//用来保存sin相关。
可以得到如下程序:
-
for(k=0;k<N;k++)
-
{
-
for(n=0;n<N;n++)
-
{
-
real[k] = real[k] + x[n] * cos(2*PI*k*n/N) ;
-
imag[k] = imag[k] – x[n] * sin(2*PI*k*n/N);
-
}
-
}
- 1
Real就是cos相关的幅值,imag就是sin相关的幅值
最后将sin与cos合成一个sin,
就完了。。。







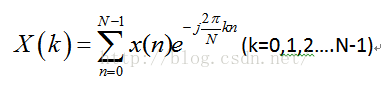
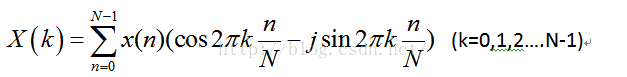
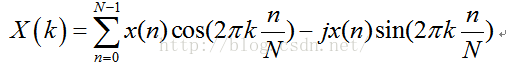
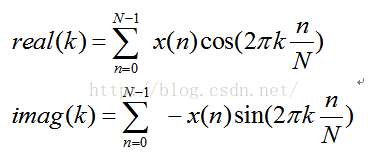














 4226
4226











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








