文章目录
实战密码学:密钥交换协议
密钥管理包括密钥的生成、分发(交换)、存储、使用、备份、归档、销毁等生命周期,密钥交换属于密钥管理中的重要一环,本次我们将给出最常用的ECDH协议、MQV协议以及国密算法SM2中的MQV变体协议。
1、ECDH密钥交换协议
基本参数: 椭圆曲线 y 2 = x 3 + a x + b ( m o d p ) y^2=x^3+ax+b \ (mod \ p) y2=x3+ax+b (mod p),六元参数组为 ( p , a , b , G , n , h ) (p, a, b, G, n, h) (p,a,b,G,n,h),含义如下:
- 有限域 F p F_p Fp
- 方程系数 a a a和 b b b
- 椭圆曲线的阶为 # E ( F p ) = n h \#E(F_p)=nh #E(Fp)=nh
- 余因子 h h h,通常是较小的数
- n n n为我们在其上进行计算的子群
1.1 ECDH协议描述
ECDH的思想比较简单,假设交互的两方分别是Alice和Bob,协议执行过程如图1所示:
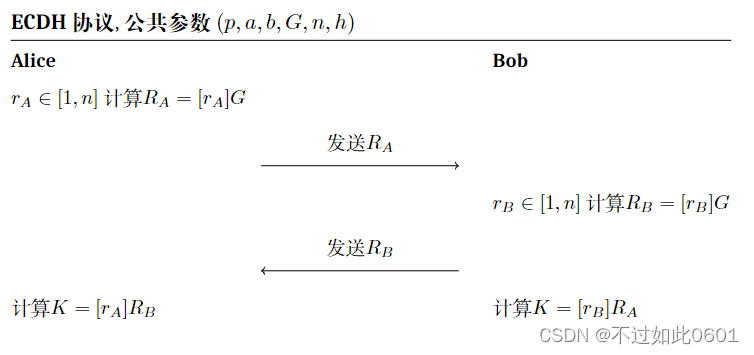
- Alice随机选取的 r A ∈ [ 1 , n ] r_A\in [1, n] rA∈[1,n],计算出 R A = [ r A ] G R_A=[r_A]G RA=[rA]G,将 R A R_A RA发送给Bob;
- Bob随机选取的 r B ∈ [ 1 , n ] r_B\in [1, n] rB∈[1,n],计算出 R B = [ r B ] G R_B=[r_B]G RB=[rB]G,将 R B R_B RB发送给Alice;
- Alice计算共享的密钥 K = [ r A ] R B K=[r_A]R_B K=[rA]RB;
- Alice计算共享的密钥
K
=
[
r
B
]
R
A
K=[r_B]R_A
K=[rB]RA;
容易看出,他们共享的密钥都是 K = [ r A ] [ r B ] G K=[r_A][r_B]G K=[rA][rB]G.
1.2 ECDH的问题
- 中间人攻击:直接使用上面的密钥交换协议会受到中间人攻击,这是因为协议中不含有任何能验证身份的信息(即使双方都有数字证书)。
- 三种解决方案:
- 一方使用固定的公私钥对,公钥为证书中认证的公钥。另一方使用临时生成的公私钥对。这样可以由证书来提供身份的认证性,避免中间人攻击。但这样的方式若某个时刻固定公钥对应的长期私钥泄露则会造成所有协商的会话密钥泄露导致所有的密文都能被解密(敌手可以缓存之前的密钥协商过程中数据以及所有通信密文),这样无法提供前向安全性(前向安全的期望是在某个时刻的密钥泄露后,之前的数据仍然是安全的),因此方案的安全性不够高。
- 双方都使用临时生成的公私钥对+数字签名,并且两方对交换的临时公钥都采用数字签名,这样接收方可以利用数字证书中的认证公钥对这个签名进行验签,从而实现身份认证,避免中间人攻击。这种方式也正是现在TLS协议中采用的方法。
- 隐式认证的密钥交换协议(如MQV)。从中间人攻击的实质可以看出,密钥交换的过程如果嵌入能够证明身份的公钥,则中间人攻击无法奏效。下一节的MQV协议正是利用了这样的思想。
1.3 MQV密钥交换协议
首先与ECDH协议一样,椭圆曲线的基本公共参数为 ( p , a , b , G , n , h ) (p, a, b, G, n, h) (p,a,b,G,n,h),此外:
- Alice的标识 I D A ID_A IDA,长期私钥 d A d_A dA,长期公钥 P A = d A ⋅ G P_A=d_A\cdot G PA=dA⋅G. 根据 I D A ID_A IDA, P A = ( x A , y A ) P_A=(x_A, y_A) PA=(xA,yA)和 G = ( x G , y G ) G=(x_G, y_G) G=(xG,yG)等信息计算Alice的哈希值 Z A = H a s h ( E N T L A ∣ ∣ I D A ∣ ∣ a ∣ ∣ b ∣ ∣ x G ∣ ∣ y G ∣ ∣ x A ∣ ∣ y A ) Z_A=Hash(ENTL_A||ID_A||a||b||x_G||y_G||x_A||y_A) ZA=Hash(ENTLA∣∣IDA∣∣a∣∣b∣∣xG∣∣yG∣∣xA∣∣yA),其中 E N T L A ENTL_A ENTLA表示 I D A ID_A IDA的长度的两个字节。
- Bob的标识 I D B ID_B IDB,长期私钥 d B d_B dB,长期公钥 P B = d B ⋅ G P_B=d_B\cdot G PB=dB⋅G. 根据 I D B ID_B IDB, P B = ( x B , y B ) P_B=(x_B, y_B) PB=(xB,yB)和 G = ( x G , y G ) G=(x_G, y_G) G=(xG,yG)等信息计算Bob的哈希值 Z B = H a s h ( E N T L B ∣ ∣ I D B ∣ ∣ a ∣ ∣ b ∣ ∣ x G ∣ ∣ y G ∣ ∣ x B ∣ ∣ y B ) Z_B=Hash(ENTL_B||ID_B||a||b||x_G||y_G||x_B||y_B) ZB=Hash(ENTLB∣∣IDB∣∣a∣∣b∣∣xG∣∣yG∣∣xB∣∣yB),其中 E N T L B ENTL_B ENTLB表示 I D B ID_B IDB的长度的两个字节。
- 令
w
=
⌈
(
⌈
(
l
o
g
2
(
n
)
⌉
/
2
)
⌉
−
1
w=\lceil(\lceil(log_2(n)\rceil/2)\rceil -1
w=⌈(⌈(log2(n)⌉/2)⌉−1,符号
⌈
⌉
\lceil\rceil
⌈⌉表示向上取整。
因此最后得到的公共参数有: ( p , a , b , G , n , h , P A , P B , Z A , Z B ) (p, a, b, G, n, h, P_A, P_B, Z_A, Z_B) (p,a,b,G,n,h,PA,PB,ZA,ZB).
协议执行过程如下图所示。

2、国密SM2的密钥交换协议
国密SM2中也给出了一个密钥交换协议,该协议和MQV协议非常相似,下面是SM2中的密钥协商协议。
2.1 国密SM2的密钥交换协议描述
椭圆曲线参数和MQV协议相同,协议的整个过程还增加可选的协商后的密钥验证部分,以确认双方协商出的密钥的确是相同的(如果没有传输和计算错误,则不执行这个验证也是可以的,实际上协商后导出的密钥理论上肯定是相同的)。协议执行如下图所示。
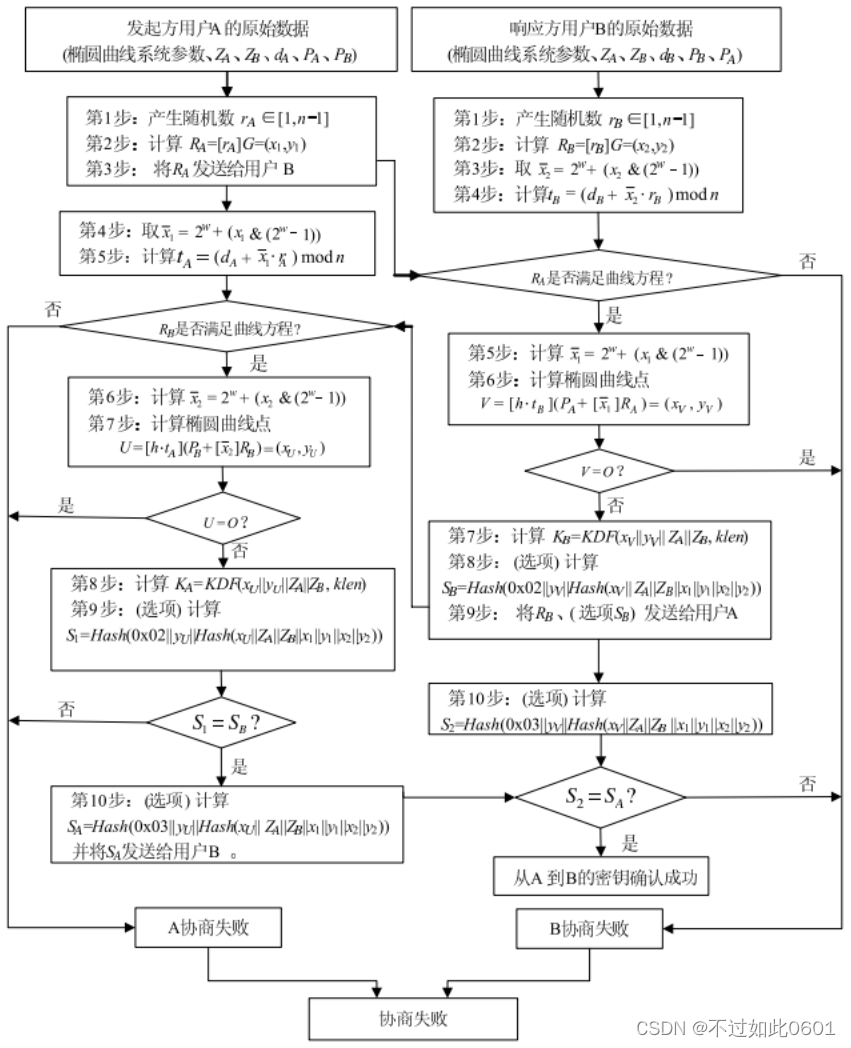
2.2 SM2密钥交换和MQV的区别
这两个方案仅在少量几个地方有差异,如下图所示。
(图片来源参考:https://blog.csdn.net/samsho2/article/details/102499148)
- 紫色高亮的部分为SM2方案。
- 青色高亮的部分为MQV方案。

3、实战部分
上面我们介绍了主流的ECDH协议、MQV协议和SM2中的密钥交换协议,下面我们的实战分为两个部分,一个是TLS中的密钥协商过程,另一个是SM2的密钥协商过程(MQV类似、省去)。
3.1 TLS中的密钥交换协议ECDHE
TLS中的密钥协议协议名称为ECDHE,最后一个E意为Ephemeral,即临时的,因为正是采用我们上面介绍的都使用临时密钥的ECDH+数字签名的方式来实现的。
TLS中的密钥协商握手协议主要有四步:
- Client端发送Client Hello,信息包括TLS版本、客户端随机数Random1、所支持的加密套件Cipher_Suit
- 服务器回复Server Hello+Certificate+Server Key Exchange+Server Hello Done,信息包括TLS版本、服务器端随机数Random2、服务器决定的加密套件、服务器证书(通常是单向认证,客户端认证服务器,所以需要服务器端发送自己的证书)、服务器端ECDH协议的公钥和对公钥的签名
- 客户端回复Client Key Exchange,信息包括客户端ECDH协议的公钥,并且发送密钥变更标志Change Cipher Spec,表示已经获取到协商的密钥ECDH Key,注意:真正的对称加密密钥是由两个随机数Random1和Random2以及ECDH Key进行KDF计算导出的。最后将之前的握手信息用这个加密密钥进行加密发送,这个Encrypted Handshake Message既可以用来验证新生成的对称密钥是否正确,也可以让服务器验证之前的握手数据是否被篡改过。
- 服务器收到客户端的 Client Key Exchange 消息后,使用客户端的ECDH公钥和两个随机数同样计算导出相同的对称加密密钥,也设置标志Change Cipher Spec,并同样发送Encrypted Handshake Message给客户端进行验证,至此TLS密钥协商握手全部完成。后续的应用数据全部进行加密传输。
整个握手过程如下图所示。
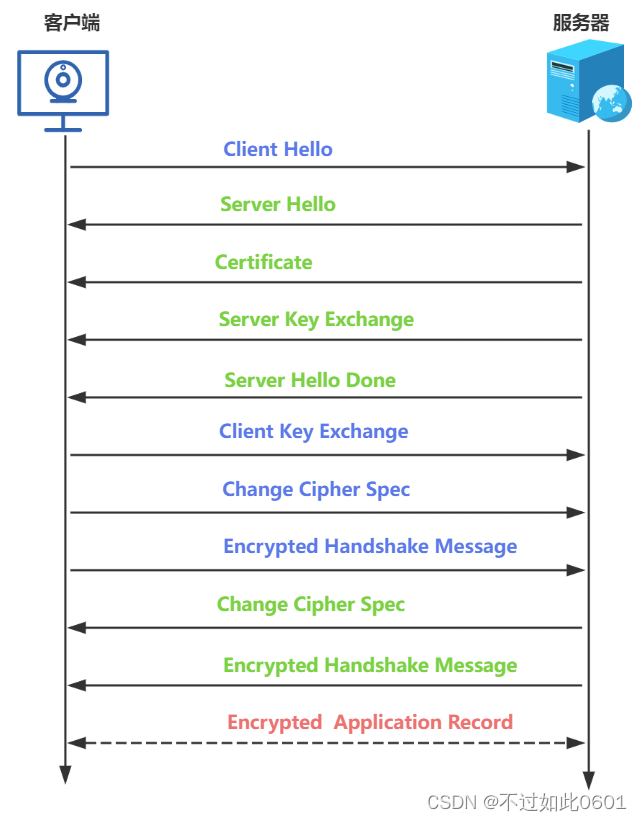
3.2 Wireshark抓包验证
(1)我们使用Wireshark进行握手过程抓包验证,首先设置Wireshark抓包WLAN。

(2)设置好后开始抓包,在浏览器上访问https://cn.bing.com/,然后找到bing网站的ip地址用户稍后过滤数据包。

同样获取本机IP地址

过滤数据包,发现TLS的握手数据

(3)查看Client Hello数据
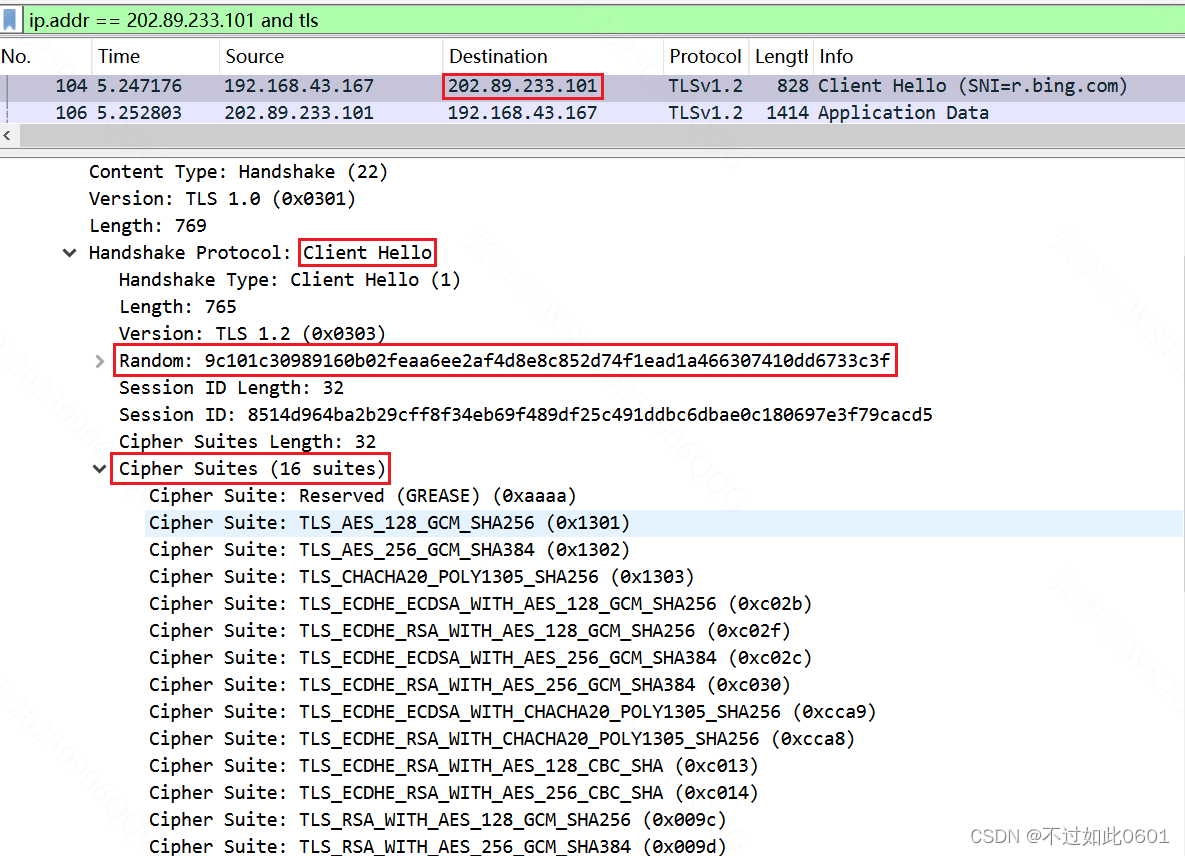
(4)Server在一个数据包中发回多个数据
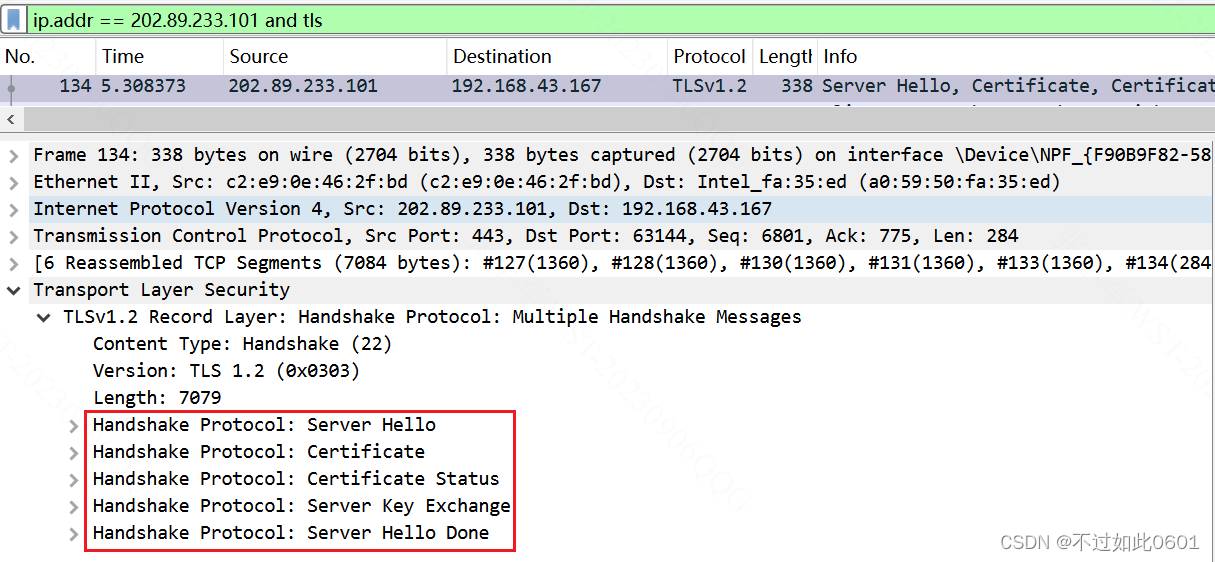
(5)查看Server Hello数据
可以看到服务器选择的密码套件为TLS_ECDHE_RSA_WITH_AES_256_GCM_SHA384,这表示使用ECDHE密钥交换协议,数字签名为RSA,之后对称加密使用256位密钥的AES,加密模式为GCM,采用的哈希函数为SHA384.
(6)查看证书Certificate数据

(7)可以看到,服务器还发回了证书状态数据,采用OCSP在线证书状态协议查询证书状态(表明证书是否有效)
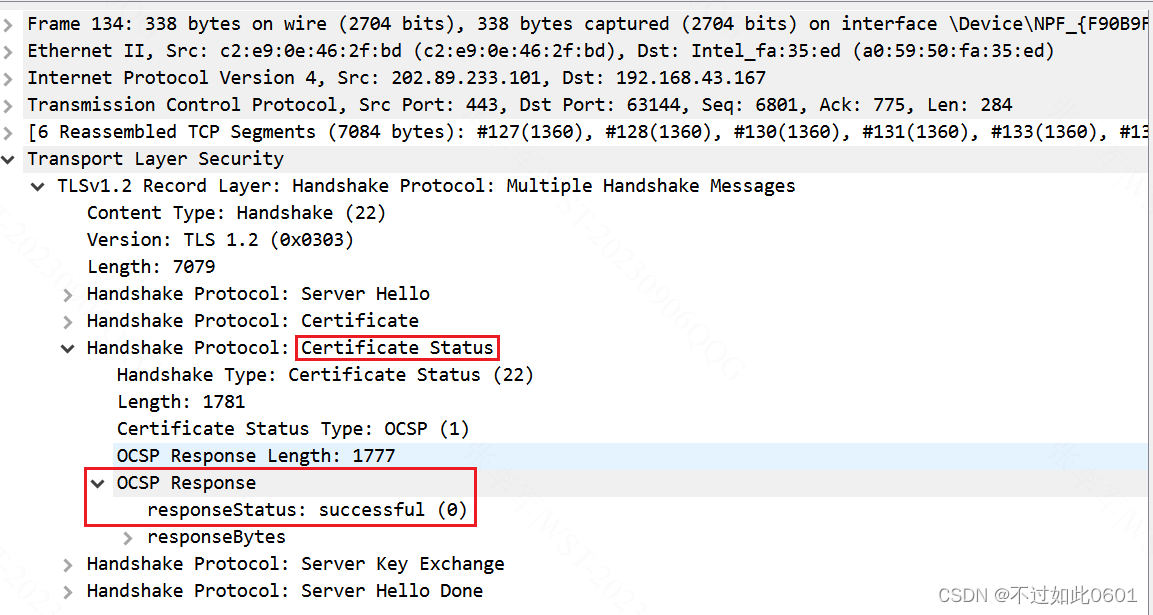
(8)查看Server Key Exchange数据

(9)查看Client发回的Key Exchange等数据

(10)查看Server发回的最后确认数据

至此TLS密钥协商的握手结束。
3.3 SM2中的密钥交换协议代码
我们使用Python来实现SM2的MQV变体密钥协商协议(GmSSL库中目前只是实现了ECDH版本,可以根据需要添加自己的MQV版本协议),参考代码来源https://blog.csdn.net/Hopeless_Loop/article/details/135534343?spm=1001.2014.3001.5502
我们测试了链接中的代码,发现我们安装的python版本的GmSSL中没有sm3_kdf的实现,只有sm3的哈希实现,因此对代码进行了修改。
下面是详细的实战步骤:
- 先安装GmSSL的C语言版本的库,这是基础,python版本的也需要调用底层C语言的库。安装很简单:
git clone https://github.com/guanzhi/GmSSL.git
cd GmSSL
mkdir build
cd build
cmake ..
make && make test
make install
安装完成后,运行gmssl version -a,若显示版本则安装成功。
- 安装python版本的GmSSL
只需执行一行命令即可。
pip install gmssl-python
- Alice方的代码如下:
import utils
import gmssl
# 用户B的ip
server_address = ("127.0.0.1", 38801)
# 用户A的身份码及其长度
id_a = "414C494345313233405941484F4F2E434F4D"
entl_a = "0090"
curve = utils.Curve()
user_a = utils.Sm2KeyAgreement(curve, id_a, entl_a)
p_a = user_a.curve.dot_to_bytes(user_a.pre_pub_key)
r_a = user_a.curve.dot_to_bytes(user_a.tem_pub_key)
z_a = user_a.id_auth_code
# 获取用户B的公钥、身份认证码和消息的sm3哈希值
user_b_data = utils.send_user_a_data_get_user_b_data(p_a, r_a, z_a, server_address)
# 提取用户B的公钥、临时会话公钥和身份认证码
p_b = user_b_data["p_b"]
r_b = user_b_data["r_b"]
z_b = user_b_data["z_b"]
v_x, v_y = user_a.key_adgreement(p_b, r_b)
alice_share = v_x + v_y + z_a + z_b
sm3 = gmssl.Sm3()
sm3.update(alice_share)
dgst = sm3.digest()
print("Alice共享的密钥为:", dgst.hex())
- Bob方的代码如下:
import utils
import gmssl
# socket绑定的ip
socket_ip = ("0.0.0.0", 38801)
id_b = "42494C4C343536405941484F4F2E434F4D"
entl_b = "0088"
curve = utils.Curve()
user_b = utils.Sm2KeyAgreement(curve, id_b, entl_b)
p_b = user_b.curve.dot_to_bytes(user_b.pre_pub_key)
r_b = user_b.curve.dot_to_bytes(user_b.tem_pub_key)
z_b = user_b.id_auth_code
# 获取用户B的公钥、身份认证码和消息的sm3哈希值
user_a_data = utils.send_user_b_data_get_user_a_data(p_b, r_b, z_b, socket_ip)
# 提取用户B的公钥、临时会话公钥和身份认证码
p_a = user_a_data["p_a"]
r_a = user_a_data["r_a"]
z_a = user_a_data["z_a"]
v_x, v_y = user_b.key_adgreement(p_a, r_a)
bob_share = v_x + v_y + z_a + z_b
sm3 = gmssl.Sm3()
sm3.update(bob_share)
dgst = sm3.digest()
print("Bob共享的密钥为:", dgst.hex())
- 相关类的代码如下:
from math import ceil, log
from sympy import isprime
import socket
import json
from random import randint
import gmssl
class Curve:
"""
椭圆曲线类,默认使用SM2手册中推荐的椭圆曲线之一。可以进行椭圆曲线上点的加法和乘法。
"""
def __init__(
self,
p=0x8542D69E4C044F18E8B92435BF6FF7DE457283915C45517D722EDB8B08F1DFC3,
a=0x787968B4FA32C3FD2417842E73BBFEFF2F3C848B6831D7E0EC65228B3937E498,
b=0x63E4C6D3B23B0C849CF84241484BFE48F61D59A5B16BA06E6E12D1DA27C5249A,
g_x=0x421DEBD61B62EAB6746434EBC3CC315E32220B3BADD50BDC4C4E6C147FEDD43D,
g_y=0x0680512BCBB42C07D47349D2153B70C4E5D7FDFCBFA36EA1A85841B9E46E09A2,
n=0x8542D69E4C044F18E8B92435BF6FF7DD297720630485628D5AE74EE7C32E79B7,
h=1,
):
self.p = p
self.a = a
self.b = b
self.g_x = g_x
self.g_y = g_y
self.n = n
self.h = h
self.bytes_len = ceil(ceil(log(self.p, 2)) / 8) * 2
def multiply(self, p, k):
"""
椭圆曲线上的倍点运算,计算 k 倍的点 p,即 [k]p
:param p: 椭圆曲线上的点,元组类型,形如 (11.0, 12.0)
:param k: 倍数 k,int类型
:return: 椭圆曲线上的点,元组类型,形如 (11.0, 12.0)
"""
return self.__from_jacobian(self.__jacobian_multiply(self.__to_jacobian(p), k))
def add(self, p, q):
"""
椭圆曲线上的加法运算,计算点 p + 点 q。即 (x1,y1)+(x2,y2)
:param p: 椭圆曲线上的点,元组类型,形如 (11.0, 12.0)
:param q: 椭圆曲线上的点,元组类型,形如 (11.0, 12.0)
:return: 椭圆曲线上的点,元组类型,形如 (11.0, 12.0)
"""
return self.__from_jacobian(
self.__jacobian_add(self.__to_jacobian(p), self.__to_jacobian(q))
)
@staticmethod
def __inv(a, n):
if a == 0:
return 0
lm, hm = 1, 0
low, high = a % n, n
while low > 1:
r = high // low
nm, new = hm - lm * r, high - low * r
lm, low, hm, high = nm, new, lm, low
return lm % n
@staticmethod
def __to_jacobian(p):
p_x, p_y = p
return p_x, p_y, 1
def __from_jacobian(self, Xp_Yp_Zp):
p_x, p_y, p_z = Xp_Yp_Zp
z = self.__inv(p_z, self.p)
return (p_x * z**2) % self.p, (p_y * z**3) % self.p
def __jacobian_double(self, p):
p_x, p_y, p_z = p
if not p_y:
return 0, 0, 0
ysq = (p_y**2) % self.p
S = (4 * p_x * ysq) % self.p
M = (3 * p_x**2 + self.a * p_z**4) % self.p
nx = (M**2 - 2 * S) % self.p
ny = (M * (S - nx) - 8 * ysq**2) % self.p
nz = (2 * p_y * p_z) % self.p
return nx, ny, nz
def __jacobian_add(self, p, q):
p_x, p_y, p_z = p
q_x, q_y, q_z = q
if not p_y:
return q_x, q_y, q_z
if not q_y:
return p_x, p_y, p_z
U1 = (p_x * q_z**2) % self.p
U2 = (q_x * p_z**2) % self.p
S1 = (p_y * q_z**3) % self.p
S2 = (q_y * p_z**3) % self.p
if U1 == U2:
if S1 != S2:
return 0, 0, 1
return self.__jacobian_double((p_x, p_y, p_z))
H = U2 - U1
R = S2 - S1
H2 = (H * H) % self.p
H3 = (H * H2) % self.p
U1H2 = (U1 * H2) % self.p
nx = (R**2 - H3 - 2 * U1H2) % self.p
ny = (R * (U1H2 - nx) - S1 * H3) % self.p
nz = (H * p_z * q_z) % self.p
return nx, ny, nz
def __jacobian_multiply(self, p, k):
p_x, p_y, p_z = p
if p_y == 0 or k == 0:
return 0, 0, 1
if k == 1:
return p_x, p_y, p_z
if k < 0 or k >= self.n:
return self.__jacobian_multiply((p_x, p_y, p_z), k % self.n)
if (k % 2) == 0:
return self.__jacobian_double(
self.__jacobian_multiply((p_x, p_y, p_z), k // 2)
)
if (k % 2) == 1:
return self.__jacobian_add(
self.__jacobian_double(
self.__jacobian_multiply((p_x, p_y, p_z), k // 2)
),
(p_x, p_y, p_z),
)
def int_to_bytes(self, x):
"""
将非负整数 x 转换为长度为 self.klen 的字节串。klen 由椭圆曲线的参数 p 在创建对象时确定。
:param x: 非负整数 x,int类型
:return: 长度为 k 的字节串,如果转换后长度小于 self.klen 则高位补 0,str类型
"""
if x < 0:
print("只能将非负整数转换为字节串!")
exit(1)
else:
return hex(x)[2:].rjust(self.bytes_len, "0")
@staticmethod
def bytes_to_int(x):
"""
将字节串 x 转换为整数
:param x: 字节串 x,str类型,形如 ac9469d628349c73
:return: 整数,int类型
"""
return int(x, 16)
@staticmethod
def bit_to_bytes(x):
"""
将比特串 x 按八位一组转换为字节串
:param x: 比特串 x,str类型,形如 000000000000111100000001
:return: 字节串,str类型,形如 0f1
"""
result = ""
i = 0
while True:
if i >= len(x):
break
else:
result += hex(int(x[i : i + 8], 2))[2:]
i += 8
return result
@staticmethod
def bytes_to_bit(x):
"""
将字节串 x 转换为比特串,每一个字节都能转换为 8 位比特串,高位补 0
:param x: 字节串 x,str类型,形如 0f1
:return: 比特串,str类型,例如 00000000 00001111 00000001
"""
result = ""
for i in x:
result += bin(int(i, 16))[2:].rjust(8, "0")
return result
def domain_element_to_bytes(self, x):
"""
将域元素转换为字节串
:param x: 域元素 x,整数,int类型;也可以为比特串,str类型。
:return: 字节串,str类型
"""
if self.p % 2 == 1 and isprime(self.p):
return self.int_to_bytes(x)
elif self.p % 2 == 0:
return self.bit_to_bytes(x)
def bytes_to_domain_element(self, x):
"""
将字节串转换为域元素
:param x: 域元素 x,整数,int类型;也可以为比特串,str类型。
:return: 域元素。如果为素域上的椭圆曲线群,则返回整数,int类型。如果为 2 的次方上的椭圆曲线群,则返回比特串,str类型。
"""
if self.p % 2 == 1 and isprime(self.p):
return self.bytes_to_int(x)
elif self.p % 2 == 0:
return self.bytes_to_bit(x)
def domain_element_to_int(self, x):
"""
将域元素转换为整数
:param x: 域元素 x,可以为整数,int类型;也可以为比特串,str类型。
:return: 整数,int类型
"""
if self.p % 2 == 1 and isprime(self.p):
return x
elif self.p % 2 == 0:
return self.bytes_to_int(self.bit_to_bytes(x))
def dot_to_bytes(self, p):
"""
将椭圆曲线上的点转换为字节串,使用未压缩形式表示。
:return: 字节串,str类型,必定以 04 开头,形如“04C424”。
"""
p_x, p_y = p
bytes_x = self.domain_element_to_bytes(p_x)
bytes_y = self.domain_element_to_bytes(p_y)
return "04" + bytes_x + bytes_y
def bytes_to_dot(self, bytes_string):
"""
将未压缩形式的字节串转换为椭圆曲线上的点
:param bytes_string: 未压缩形式的字节串,以 04 开头,str类型
:return: 横坐标 x,纵坐标 y,均为int类型。
"""
if bytes_string[:2] != "04":
print("字节串开头不为04,转换错误!")
exit(1)
else:
bytes_x = bytes_string[2 : self.bytes_len + 2]
bytes_y = bytes_string[self.bytes_len + 2 :]
x = self.bytes_to_domain_element(bytes_x)
y = self.bytes_to_domain_element(bytes_y)
return x, y
class Sm2KeyAgreement:
def __init__(self, curve, id, entl, klen=16):
"""
创建用于密钥交换的用户
:param curve: 椭圆曲线对象
:param id: 用户ID,16进制字节串,str类型
:param entl: 用户ID的长度,用4位16进制数表示,str类型,形如 0044
:param klen: 最终协商出密钥的长度,int类型
"""
self.curve = curve
self.id = id
self.entl = entl
self.tem_pri_key, self.tem_pub_key = (
self.generate_key_pair()
) # 生成临时公钥和私钥
self.pre_pri_key, self.pre_pub_key = (
self.generate_key_pair()
) # 生成永久公钥和私钥
self.klen = klen
sm3 = gmssl.Sm3()
data = [
x
for x in (
self.entl
+ self.id
+ self.curve.int_to_bytes(self.curve.a)
+ self.curve.int_to_bytes(self.curve.b)
+ self.curve.int_to_bytes(self.curve.g_x)
+ self.curve.int_to_bytes(self.curve.g_y)
+ self.curve.int_to_bytes(self.pre_pub_key[0])
+ self.curve.int_to_bytes(self.pre_pub_key[1])
).encode()
]
data_byte = bytes(data[0])
sm3.update(data_byte)
self.id_auth_code = sm3.digest().hex()
def generate_key_pair(self):
"""
生成椭圆曲线上的私钥和对应的公钥
:return: 椭圆曲线上的私钥,椭圆曲线上的公钥,int类型和元组类型,形如216546584, (321563416,2165465)
"""
# 利用随机数生成私钥
private_key = randint(1, self.curve.n - 1)
# 利用私钥和倍点运算生成公钥
public_key = self.curve.multiply((self.curve.g_x, self.curve.g_y), private_key)
return private_key, public_key
def key_adgreement(self, another_user_permanent_pub_key, another_user_tem_pub_key):
"""
进行SM2密钥交换
:param another_user_permanent_pub_key: 另外一个用户的公钥,以04开头的16进制字节串,str类型,形如04654987C5A
:param another_user_tem_pub_key: 另外一个用户的临时公钥,以04开头的16进制字节串,str类型,形如04654987C5A
:return: SM2密钥交换中的vx和vy,16进制字节串,str类型,形如2318498AC, 23165AB
"""
p_b = self.curve.bytes_to_dot(another_user_permanent_pub_key)
r_b = self.curve.bytes_to_dot(another_user_tem_pub_key)
d_a = self.pre_pri_key
r_a = self.tem_pri_key
x_1 = self.tem_pub_key[0]
x_2 = r_b[0]
y_2 = r_b[1]
w = ceil(ceil(log(self.curve.n, 2)) / 2) - 1
x1_overline = 2**w + (x_1 & (2**w - 1))
t_a = (d_a + x1_overline * r_a) % self.curve.n
# 判断接收到的用户B的公钥是否在椭圆曲线上
if (y_2**2) % self.curve.p == (
x_2**3 + self.curve.a * x_2 + self.curve.b
) % self.curve.p:
x2_overline = 2**w + (x_2 & (2**w - 1))
tem_dot = self.curve.multiply(r_b, x2_overline)
tem_dot = self.curve.add(p_b, tem_dot)
v_x, v_y = self.curve.multiply(tem_dot, self.curve.h * t_a)
v_x = self.curve.int_to_bytes(v_x)
v_y = self.curve.int_to_bytes(v_y)
return v_x, v_y
def send_user_a_data_get_user_b_data(p_a, r_a, z_a, user_b_address):
"""
通过socket传递用户A的公钥、临时会话公钥、身份认证码,并接收用户B的公钥、临时会话公钥、身份认证码
:param p_a: 用户A的公钥
:param r_a: 用户A的临时会话公钥
:param z_a: 用户A的身份认证码
:return:
"""
# 创建一个客户端套接字对象
s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
# 连接到用户B的 IP 地址和端口号
s.connect(user_b_address)
print("成功连接到服务器!")
# 接收用户B发送过来的数据
rec_data = s.recv(1024).decode()
rec_data = json.loads(rec_data)
# 向用户B发送数据
send_data = json.dumps({"p_a": p_a, "r_a": r_a, "z_a": z_a})
s.send(send_data.encode())
# 关闭套接字
s.close()
return rec_data
def send_user_b_data_get_user_a_data(p_b, r_b, z_b, bind_address):
"""
通过socket传递用户B的公钥、临时会话公钥、身份认证码,并接收用户A的公钥、临时会话公钥、身份认证码
:param p_b: 用户B的公钥
:param r_b: 用户B的临时会话公钥
:param z_b: 用户B的身份认证码
:return:
"""
# 创建一个服务端套接字对象
s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
# 绑定一个 IP 地址和端口号
s.bind(bind_address)
# 开始 TCP 监听
s.listen(5)
# 接受用户A连接
print("等待客户端连接中......")
conn, address = s.accept()
# 向用户A发送数据
send_data = json.dumps({"p_b": p_b, "r_b": r_b, "z_b": z_b})
conn.send(send_data.encode())
# 接收用户A发送回来的数据
rec_data = conn.recv(1024).decode()
rec_data = json.loads(rec_data)
# 关闭套接字
conn.close()
s.close()
return rec_data
执行代码后(先运行bob端作为服务器,再执行alice端作为客户端),可以看到两边输出相同的密钥。我们这里采用哈希值代替了KDF,只能输出特定长度的密钥值,使用KDF的话可以输出指定长度的密钥。至此,本节密钥交接协议的实战结束。
























 411
411

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








