基础算法(一)(时间复杂度)

1.时间复杂度

1. 时间复杂度是衡量算法执行时间随输入规模增长的增长率
2. 通过分析算法中基本操作的执行次数来确定时间复杂度
3. 常见的时间复杂度包括：常数时间 0(1),线性时间 0(n),对数时间0(log n),平方时间0(n^2)等
4. 在计算的时候我们关注的是复杂度的数量级,并不要求严格的表达式

• 一般我们关注的是最坏时间复杂度,用0(f(n))表示,大多数时候我们仅需估算即可
• 一般来说,评测机1秒大约可以跑2e8次运算,我们要尽可能地让我们的程序运算规模的数量级控制在1e8以内

---

2.空间复杂度

1. 空间复杂度是衡量算法执行过程中所需的存储空间随输入规模增长的增长率
2. 通过分析算法中所使用的额外存储空间的大小来确定空间复杂度
3. 常见的空间复杂度包括::常数空间0(1),线性空间0(n),对数空间0(log n),平方空间0(n^2)等

一般我们关注的是最坏空间复杂度,用0(f(n))表示,大多数时候程序占用的空间一般可以根据开的数组大小精确算出,但也存在需要估算的情况

题目一般不会卡空间,一般是卡时间

举个例子,假如题目限制128MB , 1int~32bit~4Bytes , 128MB~32*2^20int~3e7int(int a[3e7])

---

 3.分析技巧

1. 理解基本操作:基本操作可以是算术运算(加法,乘法,位运算等),比较操作,赋值操作等
2. 关注循环结构:循环是算法中常见的结构,它的执行次数对于时间复杂度的分析至关重要
3. 递归算法:递归算法的时间和空间复杂度分析相对复杂,需要确定递归的深度以及每个归调用的时间和空间开销
4. 最坏情况分析:对于时间复杂度的分析,通常考虑最坏情况下的执行时间,要考虑输入数据使得算法执行时间达到最大值的情况
5. 善用结论:某些常见算法的时间和空间复杂度已经被广泛研究和证明,可以利用这些已知结果来分析算法的复杂度

---

4.代码示例

#include<iostream>
#include<vector>
using namespace std;
int calculateSum(vector<int>& nums){
	int sum=0;
	for(int num:nums){
		sum+=sum;
	}
	return sum;
}
int main(){
	int n;
	cout<<"Enter the elements:";
	cin>>n;
	
	vector<int>nums(n);
	cout<<"Enter the element:";
	for(int i=0;i<n;++i){
		cin>>nums[i];
	}
	
	int sum=calculateSum(nums);
	cout<<"Sum of the elements:"<<sum<<endl;
	
	return 0;
}

时间复杂度：O（n）
该算法通过循环遍历数组中的每个元素，并对它们求和，因此时间复杂度与数组中的元素数量成正比。
空间复杂度：O（n）
算法使用了一个大小为n的向量来存储输入元素，所以空间复杂度与输入元素的数量成正比。

---

#include<iostream>
using namespace std;

int fibonacci(int n){
	if(n<=1)
		return n;
		
	int prev1=0; 
	int prev2=1;
	int fib=0;
	
	for(int i=2;i<=n;++i){
		fib=prev1+prev2;
		prev1=prev2;
		prev2=fib;
	}
	
	return fib;
} 

int main(){
	int n;
	cin>>n;
	
	int result=fibonacci(n);
	cout<<"Fibonacci number at position"<<n<<":"<<result<<endl;
	
	return 0;
}

 时间复杂度：O（n）
该算法使用迭代的方式计算斐波那契数列的第n个数，循环遍历n次，因此时间复杂度与n成正比。

空间复杂度：0（1）
算法只使用了常数级别的额外空间来存储变量，不随输入规模变化。

---

#include<bits/stdc++.h>
using namespace std;
using ll=long long;

int main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	
	int n;cin>>n;
	for(int i=1;i<=n;++i){
		for(int j=i;j<=n;j+=i){
			//do something with 0(1)...		
		}
	}
	
	reuturn 0;
} 

时间复杂度：O（nlogn）
这份代码中的第一重循环执行了n次，但是第二重循环执行的次数与i有关，具体来说，内部的基本操作被执行的总次数为:

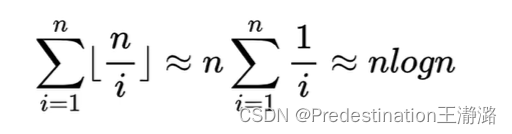
###调和级数约等于logn

空间复杂度：0（1）
算法只使用了常数级别的额外空间来存储变量，不随输入规模变化。当然这份代码并不完整，所以分析其空间复杂度意义不大。

###看似是两层循环，实际上时间复杂度优于0()

---

#include<iostream>
using namespace std;

int fibonacci(int n){
	if(n<=1){
		return n;
	}
	return fibonacci(n-1)+fibonacci(n-2);
}

int main(){
	int n;
	cout<<"Enter the value of n:";
	cin>>n;
	
	int result=fibonacci(n);
	cout<<"Fibonacci number at position"<<n<<":"<<result<<endl;
	
	return 0;
}

 时间复杂度：O（2^n）
每个递归调用会产生两个额外的递归调用，因此递归深度为2n，其中n是斐波那契数列的位置。

空间复杂度：O（n）
在非波那契数列的递归算法中，递归深度为n，因此需要的堆栈空间为O(n）。
注意:一般来说堆栈空间只给8MB，需要注意递归深度不宜过深，一般不宜超过1e6层。