算法的时间复杂度和空间复杂度-总结
通常,对于一个给定的算法,我们要做 两项分析。第一是从数学上证明算法的正确性,这一步主要用到形式化证明的方法及相关推理模式,如循环不变式、数学归纳法等。而在证明算法是正确的基础上,第二部就是分析算法的时间复杂度。算法的时间复杂度反映了程序执行时间随输入规模增长而增长的量级,在很大程度上能很好反映出算法的优劣与否。因此,作为程序员,掌握基本的算法时间复杂度分析方法是很有必要的。
算法执行时间需通过依据该算法编制的程序在计算机上运行时所消耗的时间来度量。而度量一个程序的执行时间通常有两种方法。
一、事后统计的方法
这种方法可行,但不是一个好的方法。该方法有两个缺陷:一是要想对设计的算法的运行性能进行评测,必须先依据算法编制相应的程序并实际运行;二是所得时间的统计量依赖于计算机的硬件、软件等环境因素,有时容易掩盖算法本身的优势。
二、事前分析估算的方法
因事后统计方法更多的依赖于计算机的硬件、软件等环境因素,有时容易掩盖算法本身的优劣。因此人们常常采用事前分析估算的方法。
在编写程序前,依据统计方法对算法进行估算。一个用高级语言编写的程序在计算机上运行时所消耗的时间取决于下列因素:
(1). 算法采用的策略、方法;(2). 编译产生的代码质量;(3). 问题的输入规模;(4). 机器执行指令的速度。
一个算法是由控制结构(顺序、分支和循环3种)和原操作(指固有数据类型的操作)构成的,则算法时间取决于两者的综合效果。为了便于比较同一个问题的不同算法,通常的做法是,从算法中选取一种对于所研究的问题(或算法类型)来说是基本操作的原操作,以该基本操作的重复执行的次数作为算法的时间量度。
1、时间复杂度
(1)时间频度 一个算法执行所耗费的时间,从理论上是不能算出来的,必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试,只需知道哪个算法花费的时间多,哪个算法花费的时间少就可以了。并且一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。
(2)时间复杂度 在刚才提到的时间频度中,n称为问题的规模,当n不断变化时,时间频度T(n)也会不断变化。但有时我们想知道它变化时呈现什么规律。为此,我们引入时间复杂度概念。 一般情况下,算法中基本操作重复执行的次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度,简称时间复杂度。
另外,上面公式中用到的 Landau符号其实是由德国数论学家保罗·巴赫曼(Paul Bachmann)在其1892年的著作《解析数论》首先引入,由另一位德国数论学家艾德蒙·朗道(Edmund Landau)推广。Landau符号的作用在于用简单的函数来描述复杂函数行为,给出一个上或下(确)界。在计算算法复杂度时一般只用到大O符号,Landau符号体系中的小o符号、Θ符号等等比较不常用。这里的O,最初是用大写希腊字母,但现在都用大写英语字母O;小o符号也是用小写英语字母o,Θ符号则维持大写希腊字母Θ。
T (n) = Ο(f (n)) 表示存在一个常数C,使得在当n趋于正无穷时总有 T (n) ≤ C * f(n)。简单来说,就是T(n)在n趋于正无穷时最大也就跟f(n)差不多大。也就是说当n趋于正无穷时T (n)的上界是C * f(n)。其虽然对f(n)没有规定,但是一般都是取尽可能简单的函数。例如,O(2n2+n +1) = O (3n2+n+3) = O (7n2 + n) = O ( n2 ) ,一般都只用O(n2)表示就可以了。注意到大O符号里隐藏着一个常数C,所以f(n)里一般不加系数。如果把T(n)当做一棵树,那么O(f(n))所表达的就是树干,只关心其中的主干,其他的细枝末节全都抛弃不管。
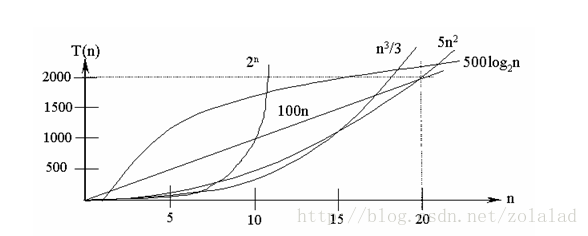
在各种不同算法中,若算法中语句执行次数为一个常数,则时间复杂度为O(1),另外,在时间频度不相同时,时间复杂度有可能相同,如T(n)=n2+3n+4与T(n)=4n2+2n+1它们的频度不同,但时间复杂度相同,都为O(n2)。 按数量级递增排列,常见的时间复杂度有:常数阶O(1),对数阶O(log2n),线性阶O(n), 线性对数阶O(nlog2n),平方阶O(n2),立方阶O(n3),..., k次方阶O(nk),指数阶O(2n)。随着问题规模n的不断增大,上述时间复杂度不断增大,算法的执行效率越低。
从图中可见,我们应该尽可能选用多项式阶O(nk)的算法,而不希望用指数阶的算法。
常见的算法时间复杂度由小到大依次为:Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<Ο(n3)<…<Ο(2n)<Ο(n!)
一般情况下,对一个问题(或一类算法)只需选择一种基本操作来讨论算法的时间复杂度即可,有时也需要同时考虑几种基本操作,甚至可以对不同的操作赋予不同的权值,以反映执行不同操作所需的相对时间,这种做法便于综合比较解决同一问题的两种完全不同的算法。
(3)求解算法的时间复杂度的具体步骤是:
⑴ 找出算法中的基本语句;
算法中执行次数最多的那条语句就是基本语句,通常是最内层循环的循环体。
⑵ 计算基本语句的执行次数的数量级;
只需计算基本语句执行次数的数量级,这就意味着只要保证基本语句执行次数的函数中的最高次幂正确即可,可以忽略所有低次幂和最高次幂的系数。这样能够简化算法分析,并且使注意力集中在最重要的一点上:增长率。
⑶ 用大Ο记号表示算法的时间性能。
将基本语句执行次数的数量级放入大Ο记号中。
如果算法中包含嵌套的循环,则基本语句通常是最内层的循环体,如果算法中包含并列的循环,则将并列循环的时间复杂度相加。例如:
for (i=1; i<=n; i++)
x++;
for (i=1; i<=n; i++)
for (j=1; j<=n; j++)
x++;
第一个for循环的时间复杂度为Ο(n),第二个for循环的时间复杂度为Ο(n2),则整个算法的时间复杂度为Ο(n+n2)=Ο(n2)。
Ο(1)表示基本语句的执行次数是一个常数,一般来说,只要算法中不存在循环语句,其时间复杂度就是Ο(1)。其中Ο(log2n)、Ο(n)、 Ο(nlog2n)、Ο(n2)和Ο(n3)称为多项式时间,而Ο(2n)和Ο(n!)称为指数时间。计算机科学家普遍认为前者(即多项式时间复杂度的算法)是有效算法,把这类问题称为P(Polynomial,多项式)类问题,而把后者(即指数时间复杂度的算法)称为NP(Non-Deterministic Polynomial, 非确定多项式)问题。
一般来说多项式级的复杂度是可以接受的,很多问题都有多项式级的解——也就是说,这样的问题,对于一个规模是n的输入,在n^k的时间内得到结果,称为P问题。有些问题要复杂些,没有多项式时间的解,但是可以在多项式时间里验证某个猜测是不是正确。比如问4294967297是不是质数?如果要直接入手的话,那么要把小于4294967297的平方根的所有素数都拿出来,看看能不能整除。还好欧拉告诉我们,这个数等于641和6700417的乘积,不是素数,很好验证的,顺便麻烦转告费马他的猜想不成立。大数分解、Hamilton回路之类的问题,都是可以多项式时间内验证一个“解”是否正确,这类问题叫做NP问题。
(4)在计算算法时间复杂度时有以下几个简单的程序分析法则:
(1).对于一些简单的输入输出语句或赋值语句,近似认为需要O(1)时间
(2).对于顺序结构,需要依次执行一系列语句所用的时间可采用大O下"求和法则"
求和法则:是指若算法的2个部分时间复杂度分别为 T1(n)=O(f(n))和 T2(n)=O(g(n)),则 T1(n)+T2(n)=O(max(f(n), g(n)))
特别地,若T1(m)=O(f(m)), T2(n)=O(g(n)),则 T1(m)+T2(n)=O(f(m) + g(n))
(3).对于选择结构,如if语句,它的主要时间耗费是在执行then字句或else字句所用的时间,需注意的是检验条件也需要O(1)时间
(4).对于循环结构,循环语句的运行时间主要体现在多次迭代中执行循环体以及检验循环条件的时间耗费,一般可用大O下"乘法法则"
乘法法则: 是指若算法的2个部分时间复杂度分别为 T1(n)=O(f(n))和 T2(n)=O(g(n)),则 T1*T2=O(f(n)*g(n))
(5).对于复杂的算法,可以将它分成几个容易估算的部分,然后利用求和法则和乘法法则技术整个算法的时间复杂度
另外还有以下2个运算法则:(1) 若g(n)=O(f(n)),则O(f(n))+ O(g(n))= O(f(n));(2) O(Cf(n)) = O(f(n)),其中C是一个正常数
(5)下面分别对几个常见的时间复杂度进行示例说明:
(1)、O(1)
Temp=i; i=j; j=temp;
以上三条单个语句的频度均为1,该程序段的执行时间是一个与问题规模n无关的常数。算法的时间复杂度为常数阶,记作T(n)=O(1)。注意:如果算法的执行时间不随着问题规模n的增加而增长,即使算法中有上千条语句,其执行时间也不过是一个较大的常数。此类算法的时间复杂度是O(1)。
(2)、O(n2)
2.1. 交换i和j的内容
sum=0; (一次)
for(i=1;i<=n;i++) (n+1次)
for(j=1;j<=n;j++) (n2次)
sum++; (n2次)解:因为Θ(2n2+n+1)=n2(Θ即:去低阶项,去掉常数项,去掉高阶项的常参得到),所以T(n)= =O(n2);
2.2.
for (i=1;i<n;i++)
{
y=y+1; ①
for (j=0;j<=(2*n);j++)
x++; ②
} 解: 语句1的频度是n-1
语句2的频度是(n-1)*(2n+1)=2n2-n-1
f(n)=2n2-n-1+(n-1)=2n2-2;
又Θ(2n2-2)=n2
该程序的时间复杂度T(n)=O(n2).
一般情况下,对步进循环语句只需考虑循环体中语句的执行次数,忽略该语句中步长加1、终值判别、控制转移等成分,当有若干个循环语句时,算法的时间复杂度是由嵌套层数最多的循环语句中最内层语句的频度f(n)决定的。
(3)、O(n)
a=0;
b=1; ①
for (i=1;i<=n;i++) ②
{
s=a+b; ③
b=a; ④
a=s; ⑤
}解: 语句1的频度:2,
语句2的频度: n,
语句3的频度: n-1,
语句4的频度:n-1,
语句5的频度:n-1,
T(n)=2+n+3(n-1)=4n-1=O(n).
(4)、O(log2n)
i=1; ①
while (i<=n)
i=i*2; ②解: 语句1的频度是1,
设语句2的频度是f(n), 则:2^f(n)<=n;f(n)<=log2n
取最大值f(n)=log2n,
T(n)=O(log2n )
(5)、O(n3)
for(i=0;i<n;i++)
{
for(j=0;j<i;j++)
{
for(k=0;k<j;k++)
x=x+2;
}
}解:当i=m, j=k的时候,内层循环的次数为k当i=m时, j 可以取 0,1,...,m-1 , 所以这里最内循环共进行了0+1+...+m-1=(m-1)m/2次所以,i从0取到n, 则循环共进行了: 0+(1-1)*1/2+...+(n-1)n/2=n(n+1)(n-1)/6所以时间复杂度为O(n3).
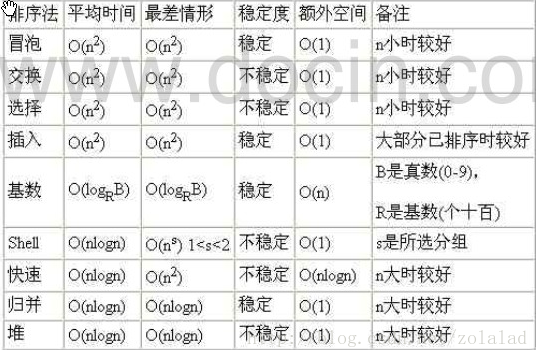
(5)常用的算法的时间复杂度和空间复杂度
一个经验规则:其中c是一个常量,如果一个算法的复杂度为c 、 log2n 、n 、 n*log2n ,那么这个算法时间效率比较高 ,如果是2n ,3n ,n!,那么稍微大一些的n就会令这个算法不能动了,居于中间的几个则差强人意。
算法时间复杂度分析是一个很重要的问题,任何一个程序员都应该熟练掌握其概念和基本方法,而且要善于从数学层面上探寻其本质,才能准确理解其内涵。
2、算法的空间复杂度
类似于时间复杂度的讨论,一个算法的空间复杂度(Space Complexity)S(n)定义为该算法所耗费的存储空间,它也是问题规模n的函数。渐近空间复杂度也常常简称为空间复杂度。
空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。一个算法在计算机存储器上所占用的存储空间,包括存储算法本身所占用的存储空间,算法的输入输出数据所占用的存储空间和算法在运行过程中临时占用的存储空间这三个方面。算法的输入输出数据所占用的存储空间是由要解决的问题决定的,是通过参数表由调用函数传递而来的,它不随本算法的不同而改变。存储算法本身所占用的存储空间与算法书写的长短成正比,要压缩这方面的存储空间,就必须编写出较短的算法。算法在运行过程中临时占用的存储空间随算法的不同而异,有的算法只需要占用少量的临时工作单元,而且不随问题规模的大小而改变,我们称这种算法是“就地\"进行的,是节省存储的算法,如这一节介绍过的几个算法都是如此;有的算法需要占用的临时工作单元数与解决问题的规模n有关,它随着n的增大而增大,当n较大时,将占用较多的存储单元,例如将在第九章介绍的快速排序和归并排序算法就属于这种情况。
如当一个算法的空间复杂度为一个常量,即不随被处理数据量n的大小而改变时,可表示为O(1);当一个算法的空间复杂度与以2为底的n的对数成正比时,可表示为0(10g2n);当一个算法的空I司复杂度与n成线性比例关系时,可表示为0(n).若形参为数组,则只需要为它分配一个存储由实参传送来的一个地址指针的空间,即一个机器字长空间;若形参为引用方式,则也只需要为其分配存储一个地址的空间,用它来存储对应实参变量的地址,以便由系统自动引用实参变量。
参考1:http://www.cnblogs.com/songQQ/archive/2009/10/20/1587122.html
参考2 :http://www.cppblog.com/85940806/archive/2011/03/12/141672.html
























 1038
1038

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








