逻辑回归——python实例

最新推荐文章于 2025-04-04 07:45:29 发布

大太阳小白

最新推荐文章于 2025-04-04 07:45:29 发布

阅读量2.5k

点赞数 2

分类专栏：机器学习文章标签：机器学习 python 逻辑回归

本文链接：https://blog.csdn.net/weixin_41579863/article/details/110859335

版权

机器学习专栏收录该内容

13 篇文章

订阅专栏

本文介绍了线性可分的概念，通过芝诺悖论的例子阐述了线性分类问题。接着详细讲解了逻辑回归模型，包括Sigmoid函数的作用、损失函数的构建以及最大似然估计在参数估计中的应用。通过梯度下降法求解最优参数，并讨论了凸函数与非凸函数在优化过程中的影响。最后，以糖尿病预测数据集为例展示了逻辑回归的训练和预测流程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题外话——芝诺悖论

只要乌龟在起点拥有些许领先优势的话，兔子将永远追不上乌龟，甚至可以得到乌龟跟兔子无法抵达终点的悖论。来自——《The Math Book》

例如:起点到终点的距离是1，一定时间走了1/2，再过一段时间走了剩下路程的1/2....以此类推，它将无法走到终点。

《庄子·天下篇》中也提到：“一尺之棰，日取其半，万世不竭。”

言归正传

什么是线性可分

通常情况下一个分类问题可以分成线性可分和线性不可分两种，下面是它们的图像表示：

什么是逻辑回归

英文Logistic Regression，是广义线性模型的一种，属于线性的分类模型。核心思想是找一条直线将两个不同类别分开。

已知一个超平面的函数表达如下：Wx + b，其中W是权重，x样本特征，b是偏置。当我们得到这个超平面可以将数据分成两类，这时需要一个阈值函数或叫联系函数，将

样本映射到不同的类别中。

常用的阈值函数有Sigmoid函数： $f(x) = \frac{1}{1+e^{-x}}$

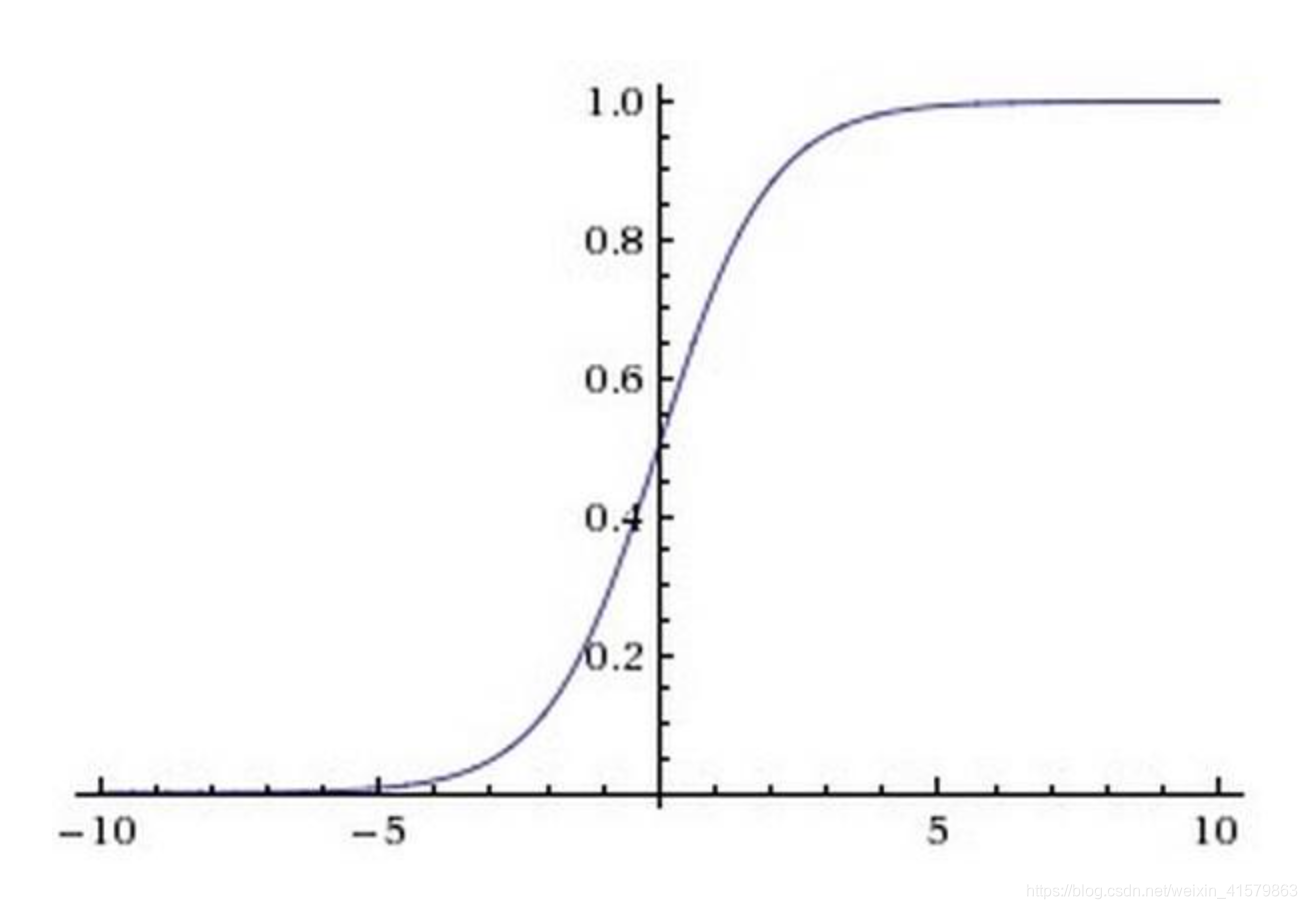
使用Sigmoid函数有两点好处：

1）值域在（0,1）x小于0时，y无限接近0；x大于0时，y无限接近1；那么通常情况下以x=0为分界线，当y>1/2时认为正例，y<=1/2时认为负例

2）模型推导需要损失函数的导数，为了减少计算复杂度，sigmoid函数的导数和函数本身有关。

推导过程：

逻辑回归模型表示

我们将平面的的线性表示加入到sigmoid函数中则：

P0（y =1 | X，W，b）= $\frac{1}{1+e^{-(WX+b)}}$

P1（y =0 | X，W，b）=1-P0（y =1 | X，W，b）= $\frac{e^{-(WX+b)}}{1+e^{-(WX+b)}}$

关于此二分类问题，统计学上称为伯努利分布，因为结果只有正、负两种可能，即p 和 1-p，所以概率函数可以用下面方式表达

$P(y|p) = p^{y}+(1-p)^{1-y}$ ，其中y = 0,1

所以回归模型可以表示为

$P(y|X,W,b)=(\frac{1}{1+e^{-(WX+b)}})^{y}*(1-\frac{1}{1+e^{-(WX+b)}})^{1-y}$

参数估计

通过上述描述该问题是个后验概率问题，即已知果求因，利用最大似然法估计W，b参数。

最大似然估计

最大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。

最大似然估计的一般求解过程：

　　（1）写出似然函数；

　　（2）对似然函数取对数，并整理；

　　（3）求导数；

　　（4）解似然方程

似然函数

$L_{w,b}=\prod P(y|X,W,b)=\prod ((\frac{1}{1+e^{-(WX+b)}})^{y}*(1-\frac{1}{1+e^{-(WX+b)}})^{1-y})$

最大似然是在寻找所有可能的w,b使函数最大，求得最大似然函数下的w,b取值，所以maxL(w,b)通过对数变换可以转换成l(w,b)最小值

即求 $\small w*,b* =argmin(lw,b)$ 的过程，w*，b*表示参数的解

根据法则：

转换后的似然函数对数形式： $\small l_{w,b}=-\sum (yln (\frac{1}{1+e^{-(WX+b)}})+(1-y)ln(1-\frac{1}{1+e^{-(WX+b)}})))$

整理，当y = 1时候

$\small l_{w,b}=-\sum ln (\frac{1}{1+e^{-(WX+b)}})$

当y = 0 时候

$\small l_{w,b}=-\sum ln(1-\frac{1}{1+e^{-(WX+b)}}) = -\sum ln(\frac{e^{-(wx+b)}}{1+e^{-(wx+b)}}) = -\sum (-(wx+b)+ln\frac{1}{1+e^{-(wx+b)}})$

合并：

$\small l_{w,b}= -\sum ln(\frac{e^{-(wx+b)}}{1+e^{-(wx+b)}}) = -\sum (-(1-y)(wx+b)+ln\frac{1}{1+e^{-(wx+b)}})=-\sum (y-1)(wx+b)+lne^{wx+b}+ln(1+e^{wx+b})=-\sum ywx+b+ln(1+e^{wx+b})$

到此逻辑回归的损失函数已经整理完成，即上式结果。

梯度下降法

梯度下降法通过对上面的损失函数进行优化，寻找最优参数w的过程，寻找方向就是当前点损失函数的梯度方向。

对数似然函数（损失函数）求导：

$\small \frac{\partial l}{\partial w}=\sum x(\frac{1}{1+e^{wx+b}}-y)$ ，其中x理解为数据的特征向量，y是标注值， $\small \frac{1}{1+e^{wx+b}}$ 是上面的P1，是要经过迭代计算出来的。若w0=b，x0设置为1，则偏置项b可以省略，

导数可以写成 $\small \frac{\partial l}{\partial w}=\sum x(\frac{1}{1+e^{wx}}-y)$

梯度下降法一般流程：

随机初始化一个参数w

for 损失到达阈值或迭代一定次数：

选择步长a
决定梯度下降方向： $\small di= -\frac{\partial l(w)}{\partial w}|_{wi}$ ，表示wi位置的梯度值
更新权重： $\small w_{i+1} =w_{i} +a*di$

凹函数与非凸函数

这里涉及一个问题，通过梯度下降法能否得到像上图那样全局最优点，这便引出另一个知识点凸函数问题。

左面是凸函数，有全局最优点，右边是非凸函数，有全局最优点和局部最优点，如果是非凸函数，求得的解有可能不是最优解（即局部最优解）。

如果判断是否是凸函数

对于一元函数f(x)，我们可以通过其二阶导数f′′(x) 的符号来判断。如果函数的二阶导数总是非负，即f′′(x)≥0 ，则f(x)是凸函数

对于多元函数f(X)，我们可以通过其Hessian矩阵（Hessian矩阵是由多元函数的二阶导数组成的方阵）的正定性来判断。如果Hessian矩阵是半正定矩阵，则是凸函数。

实例

引用数据

该数据集源至美国国家糖尿病、消化及肾脏疾病研究所。数据集的目的是根据已有诊断信息来预测患者是否患有糖尿病。但该数据库存在一定局限性，特别是数据集中的患者都是年龄大于等于21岁的皮马印第安女性。

涉及字段如下：其中Outcome标注字段，代表是否是糖尿病人。

数据地址1：https://www.kaggle.com/uciml/pima-indians-diabetes-database

数据地址2：https://github.com/susanli2016/Machine-Learning-with-Python/blob/master/diabetes.csv

在这里插入图片描述

定义sigmoid函数

def sigmoid(w,x):
    """
    定义sigmoid函数
    :param x:
    :param w:
    :return:
    """
    return 1/(1+np.exp(-(w*x)))

定义模型训练

def train(x,y,iter_max= 1000,alpha = 0.00001):
    """
    模型训练逻辑
    :param x:
    :param y:
    :param iter_max:
    :param alpha:
    :return:
    """
    size = np.shape(x)[1]
    w = np.mat(np.ones((size,1)))
    for _ in range(iter_max):
        p0 = sigmoid(w.T,x.T)
        w_derivative =(p0-y)* x
        w = w+(alpha*w_derivative).T
    return w

准确率定义

def accuracy(y,label):
    m_size = len(label)
    accuracy_num = (y^label).sum()
    return 1-accuracy_num/m_size

模型预测

def predict(weights,input_x):
    y = sigmoid(weights.T,input_x.T)
    return np.array((y.T>0.5).reshape(-1))[0].astype(int)

数据标准化

train_data = df_train.values
    test_data = df_test.values
    col_num = np.shape(train_data)[1]-1
    for index in range(col_num):
        std_v = train_data[:,index].std()
        mean_v = train_data[:,index].mean()
        train_data[:, index] = (train_data[:,index]-mean_v)/std_v
        test_data[:, index] = (test_data[:,index]-mean_v)/std_v
    x,y = train_data[:,:-1],train_data[:,-1]
    weights= train(x,y)
    test_x,test_label = test_data[:,:-1],test_data[:,-1]
    test_y = predict(weights,test_x)
    accuracy_rate = accuracy(test_y,test_label.astype(int))

切分数据集

data = pd.read_csv('diabetes.csv')
df = data.sample(frac=1.0)  # 全部打乱
cut_idx = int(round(0.1 * df.shape[0]))
df_test, df_train = df.iloc[:cut_idx], df.iloc[cut_idx:]

基本思路就这样，代码暂未整理，有时间整理一下吧