
二元信号检测理论模型
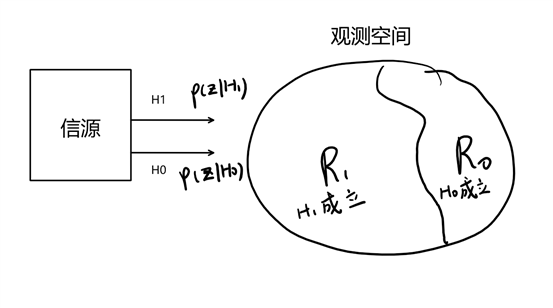
判决域
 1.3.1贝叶斯准则与似然比检验
1.3.1贝叶斯准则与似然比检验
代价因子
| 判决 假设 | H0 | H1 |
| H0 |
|
|
| H1 |
|
|
二元假设检验时的代价因子
在判决概率为![]() ,代价因子为
,代价因子为![]() ,在
,在![]() 判为真时所付出的代价为
判为真时所付出的代价为
![]() ,j=0,1
,j=0,1
再考虑假设![]() 出现的先验概率
出现的先验概率![]() ,则判决所付的总平均代价(又称平均风险)为
,则判决所付的总平均代价(又称平均风险)为
![]()
所谓贝叶斯准则,就是在假设Hj的先验概率已知,各代价因子给定时,使平均代价最小的准则。
由检测理论模型和判决域划分可知,平均代价可以通过转移概率密度函数及判决域来表示:

其中,z是N维随机矢量。由于
![]()
![]()
![]()
因此R1域的积分项可表示为:
![]()
所以,平均代价可以表示为

上式第一第二项为固定平均代价分量,与判决域划分无关,式中积分项是平均代价可变部分,它的正负受积分区域R0控制。根据贝叶斯准则,应使平均代价最小,为此将凡是使被积函数取负值的那些z值划分给R0域,而把其余的z值给R1域。即,所有满足:
![]()
的z值划分给R0,判决H0成立,其他z值划分给R1,判决H1成立,于是将上式改写,得到贝叶斯判决准则:

上面这个不等式左边是两个转移概率密度函数(又称似然函数)之比,称为似然比(likelihood ratio),用![]() 表示,即
表示,即

而不等式右边是由先验概率和代价因子决定的常数,称为似然比检测门限,记为
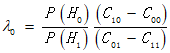
于是由贝叶斯准则得到的似然比检验(likelihood ratio test)为
![]()
![]() 和
和![]() 是N维随机矢量z的函数,而
是N维随机矢量z的函数,而![]() 是条件概率密度之比,,因此不论z的正负和维数如何,
是条件概率密度之比,,因此不论z的正负和维数如何,![]() 都是非负的一维变量;由于
都是非负的一维变量;由于![]() 是随机观测量z的函数且不含任何未知参量,因而
是随机观测量z的函数且不含任何未知参量,因而![]() 也是随机变量,我们称之为检验统计量。
也是随机变量,我们称之为检验统计量。
由其定义式可知,似然比检验需要对观测量z进行处理,即计算似然比![]() ,然后跟某个似然比检测门限
,然后跟某个似然比检测门限![]() 比较,以做出判决。
比较,以做出判决。
门限和![]() 和
和![]() 有关,为了在不同先验概率和不同代价因子时,都能达到贝叶斯准则下的最小平均代价,就应该按其定义式对门限做出调整。
有关,为了在不同先验概率和不同代价因子时,都能达到贝叶斯准则下的最小平均代价,就应该按其定义式对门限做出调整。
又由于似然比![]() 在很多情况下具有指数函数的形式,因为自然对数是单调的增函数,并且
在很多情况下具有指数函数的形式,因为自然对数是单调的增函数,并且![]() 和
和![]() 非负,所以判决可等价为:
非负,所以判决可等价为:
![]()
得如下似然比处理器

 1.3.2 贝叶斯准则的几种派生准则
1.3.2 贝叶斯准则的几种派生准则
贝叶斯准则中,对先验概率P(H)和代价因子C作某些约束下,会得到使用范围确定,更加简明的派生准则。
 1.3.2.1 最小总错误概率准则和最大似然准则
1.3.2.1 最小总错误概率准则和最大似然准则
在通信系统中,通常正确判决不付出代价,错误判决付出代价相同,这时平均代价为:

该式恰好是总(平均)错误概率。因此平均代价最小等于总错误概率最小。
类似于贝叶斯准则的分析方法,上式可改写为
![]()
将所有满足
![]()
的z值划归R0域判决H0成立;而把所有满足
![]()
的z值划归R1域,判决R1成立。即:

假设H0和H1的先验概率相等,即 ,则似然比检验为
,则似然比检验为

或写成两似然函数直接比较的形式,即
![]()
此时,可将等先验概率准则称为最大似然准则。
 1.3.2.2 最大后验概率准则
1.3.2.2 最大后验概率准则
在贝叶斯准则中,当代价因子满足![]() 时,判决规则便成为
时,判决规则便成为

或等价写成
![]()
因为

当dz很小时有

从而得

即
![]()
同样可得
![]()
于是
![]()
即
![]()
上式为当观测量z已经获得得条件下,假设H1和H0成立的概率,即后验概率。
 1.3.2.3 极大极小化准则
1.3.2.3 极大极小化准则
要使用贝叶斯准则,除了规定各代价因子Cij外,还必须知道假设H1和假设H0的先验概率。当无法确定各假设的先验概率P(Hj)时,就不能应用贝叶斯准则。现在讨论的极大极小化准则就是在已经规定了代价因子Cij但无法确定先验概率P(Hj)条件下制定的一种准则。极大极小准则能使判决在上述条件下避免可能产生过大的代价,使极大可能代价极小化。
为表达方便,重申:

如果代价因子Cij已经规定,但假设H1的先验概率P1未知,则式

表示的贝叶斯平均代价可以表示为![]() 的函数,因此似然比检测门限是
的函数,因此似然比检测门限是![]() 的函数,即
的函数,即![]() 因此此时
因此此时![]() 和
和![]() 也是
也是![]() 的函数,记为
的函数,记为![]() 和
和![]() 。因此将平均代价写为先验函数
。因此将平均代价写为先验函数![]() 的函数:
的函数:
 可以证明,当似然比
可以证明,当似然比![]() 具有严格单调概率分布随机变量时,上式表示的贝叶斯平均代价是
具有严格单调概率分布随机变量时,上式表示的贝叶斯平均代价是![]() 的严格上凸函数,如C-P1曲线图所示的曲线a。
的严格上凸函数,如C-P1曲线图所示的曲线a。

C-P1曲线
现在来考虑不知道先验概率![]() 时的情况,在这种情况下,为了能使用贝叶斯准则,只能猜测一个先验概率
时的情况,在这种情况下,为了能使用贝叶斯准则,只能猜测一个先验概率![]() ,然后用它来确定贝叶斯准则的似然比检测门限
,然后用它来确定贝叶斯准则的似然比检测门限![]() ,并以此固定门限进行判决。所以此时
,并以此固定门限进行判决。所以此时![]() 和
和![]() 也是
也是![]() 的函数,记为
的函数,记为![]() 和
和![]() 。一旦
。一旦![]() 猜定后,
猜定后,![]() 和
和![]() 就固定了,因为二者只与判决域划分有关,而判决域划分与似然比检测门限有关,似然比检测门限又与猜测的先验概率
就固定了,因为二者只与判决域划分有关,而判决域划分与似然比检测门限有关,似然比检测门限又与猜测的先验概率![]() 有关,此时平均代价和实际的先验概率
有关,此时平均代价和实际的先验概率![]() 的关系将是一条直线:
的关系将是一条直线:

当![]() 时,即猜的的先验概率恰好等于实际的先验概率时,平均代价最小(即贝叶斯平均代价),此时
时,即猜的的先验概率恰好等于实际的先验概率时,平均代价最小(即贝叶斯平均代价),此时![]() 是一条与曲线a相切的直线,切点在
是一条与曲线a相切的直线,切点在![]() 处。除
处。除![]() 点处,在其他
点处,在其他![]() 处,
处,![]() 将大于贝叶斯平均代价
将大于贝叶斯平均代价![]() ,而且对于某些可能的
,而且对于某些可能的![]() 值,例如图中的
值,例如图中的![]() ,实际的平均代价远大于最小的平均代价。为了避免这种过分大的代价,人们猜测先验概率为
,实际的平均代价远大于最小的平均代价。为了避免这种过分大的代价,人们猜测先验概率为![]() ,使该处的
,使该处的![]() 是一条与
是一条与![]() 水平相切的直线。如图中的切线c。虽然该处贝叶斯准则的最小平均代价最大,为
水平相切的直线。如图中的切线c。虽然该处贝叶斯准则的最小平均代价最大,为![]() ,但是可以使得由于未知先验概率
,但是可以使得由于未知先验概率![]() 而可能产生的那种极大平均代价
而可能产生的那种极大平均代价 ![]() 极小化,等于
极小化,等于![]() 。因此对实际的先验概率
。因此对实际的先验概率![]() ,平均代价都等于
,平均代价都等于![]() ,不会产生更大平均代价!
,不会产生更大平均代价!
为了求出极大极小化准则应满足的条件。或者说为了求得![]() ,可将
,可将![]() 或
或![]() 对
对![]()
求偏导,令结果等于0,对![]() 是斜率为0,对
是斜率为0,对![]() 来说是求极点。即
来说是求极点。即

从而得
![]()
上式可以称作准则的极大极小化方程,解此方程可以求得![]() 和似然比检测门限
和似然比检测门限![]() 。
。
此时平均代价为:
![]()
如果代价因子![]() 则极大极小方程为
则极大极小方程为
![]()
平均代价为
![]()
进而如果![]() ,
,![]() ,则有
,则有
![]()
并且极大极小化代价就是总错误概率即![]() 。
。
个人小结:
先验概率控制门限,猜测的先验概率不一定正确,即使正确也因为实际的观测z存在误差而有代价,那么猜错时肯定误差更大。这个算法的核心思想个人理解是将与人主观臆断有关的因素带来的代价降到最小。
这是一个多么无奈的算法啊!为了一个存在但未知的信息,利用![]() 对
对![]() 上凸函数的性质,将真实代价最坏的地方作为我们的猜测。足以见得信息对于人类的价值。
上凸函数的性质,将真实代价最坏的地方作为我们的猜测。足以见得信息对于人类的价值。
 1.3.2.4 奈曼-皮尔逊准则
1.3.2.4 奈曼-皮尔逊准则
使用贝叶斯准则要知道各假设的先验概率P(Hj),并对某种可能的判决赋予代价因子Cij。在先验概率不知道的情况下,可使用极大极小化准则,但在有些情况下,如雷达信号检测,要知道先验概率和指定代价是很困难的。
这种情况希望虚警概率PF尽量小,检测概率PD尽量大,实际上,若正确的检测概率PD最大,则漏报概率PM最小,但是,PM的减小又会使PF增大,因此各个概率之间的希望是矛盾的。为此,提出如下准则;
在虚警概率![]() 的约束条件下,使得检测概率
的约束条件下,使得检测概率![]() 最大(或
最大(或![]() 最小)
最小)
应用拉格朗日(Largrange)乘子μ(μ>=0)构造一个目标函数:
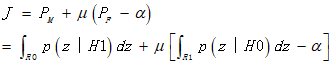
显然,若![]() 则
则![]() 达到最小,
达到最小,![]() 达到最小。变换积分域,上式变为:
达到最小。变换积分域,上式变为:
![]()
因为μ>0,因此上式中第一项为正数,要使![]() 达到最小,则令积分号里的项为负的z点划到R0域,判R0成立,反之。即:
达到最小,则令积分号里的项为负的z点划到R0域,判R0成立,反之。即:
![]() ,H1
,H1
![]() ,H0
,H0
写出似然比检验的形式为:
 ,H1
,H1
 ,H0
,H0
为了满足![]() 的约束,选择μ使得
的约束,选择μ使得
![]()
对于给定的α,μ可以从上式求出。
又
![]()
![]()
显然μ增加,PF减小,PM增加;μ减小,PF增加,PM减小。这就是说,改变μ就能调整判决域R0和R1。
N-P准则可以看作是贝叶斯准则在![]() ,
,![]() 时的特例。
时的特例。
 1.3.2.5 似然比检验的特性——ROC
1.3.2.5 似然比检验的特性——ROC
前几节讨论了几种重要的判决规则,并导出相应的判决规则表示式,这些准则都要求计算似然比![]() ,这些准则有各自最佳性能指标,并体现在门限
,这些准则有各自最佳性能指标,并体现在门限![]() 上。贝叶斯准则要求平均代价最小,最小错误概率准则要求总错误概率最小,而纽曼皮尔逊准则要求在虚警概率
上。贝叶斯准则要求平均代价最小,最小错误概率准则要求总错误概率最小,而纽曼皮尔逊准则要求在虚警概率![]() 的约束下,检测概率
的约束下,检测概率![]() 最大,从而可确定不同的
最大,从而可确定不同的![]() 值,分析它们各自的“最佳”性能指标可以看出,不论哪种准则其检测性能的优劣都体现在虚警概率PF和检测概率PD上。
值,分析它们各自的“最佳”性能指标可以看出,不论哪种准则其检测性能的优劣都体现在虚警概率PF和检测概率PD上。

接收机工作特性曲线-20dBà12dB
对于不同的信噪比,有不同的![]() 曲线,但是他们都通过
曲线,但是他们都通过![]() 及
及![]() 两点,并位于直线
两点,并位于直线![]() 左上方的上凸曲线。信噪比越大,曲线位置就月高。
左上方的上凸曲线。信噪比越大,曲线位置就月高。
这些曲线反映了![]() 和
和![]() 与检测门限
与检测门限![]() 及信噪比的关系,所以
及信噪比的关系,所以![]() 曲线描述了鸡舍检验的性能,称它为接收机工作特性(ROC,Receiver Operating Characteristic)。
曲线描述了鸡舍检验的性能,称它为接收机工作特性(ROC,Receiver Operating Characteristic)。
虽然观测空间R中的随机矢量![]() 的类型可能有所不同,但ROC却总具有大致的形状。如果似然比
的类型可能有所不同,但ROC却总具有大致的形状。如果似然比![]() 是
是![]() 的连续函数,则ROC有如下共同性质:
的连续函数,则ROC有如下共同性质:
l 所有连续似然比检验的ROC都是上凸的
l 所有连续似然比检验的ROC都位于对角线![]() 之上
之上
l ROC在某一特定点处的斜率等于该点上的![]() 和
和![]() 所要求的门限值
所要求的门限值![]()
证明:
![]()
![]() and
and ![]()
![]()
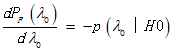 and
and 
![]()
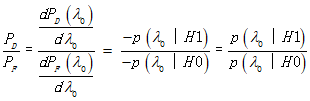
![]()
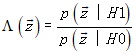
![]()

![]()

![]()
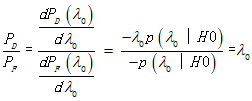
![]()
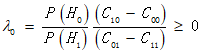
![]()
![]()
l ROC是似然比检测性能的完整描述























 1591
1591

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








