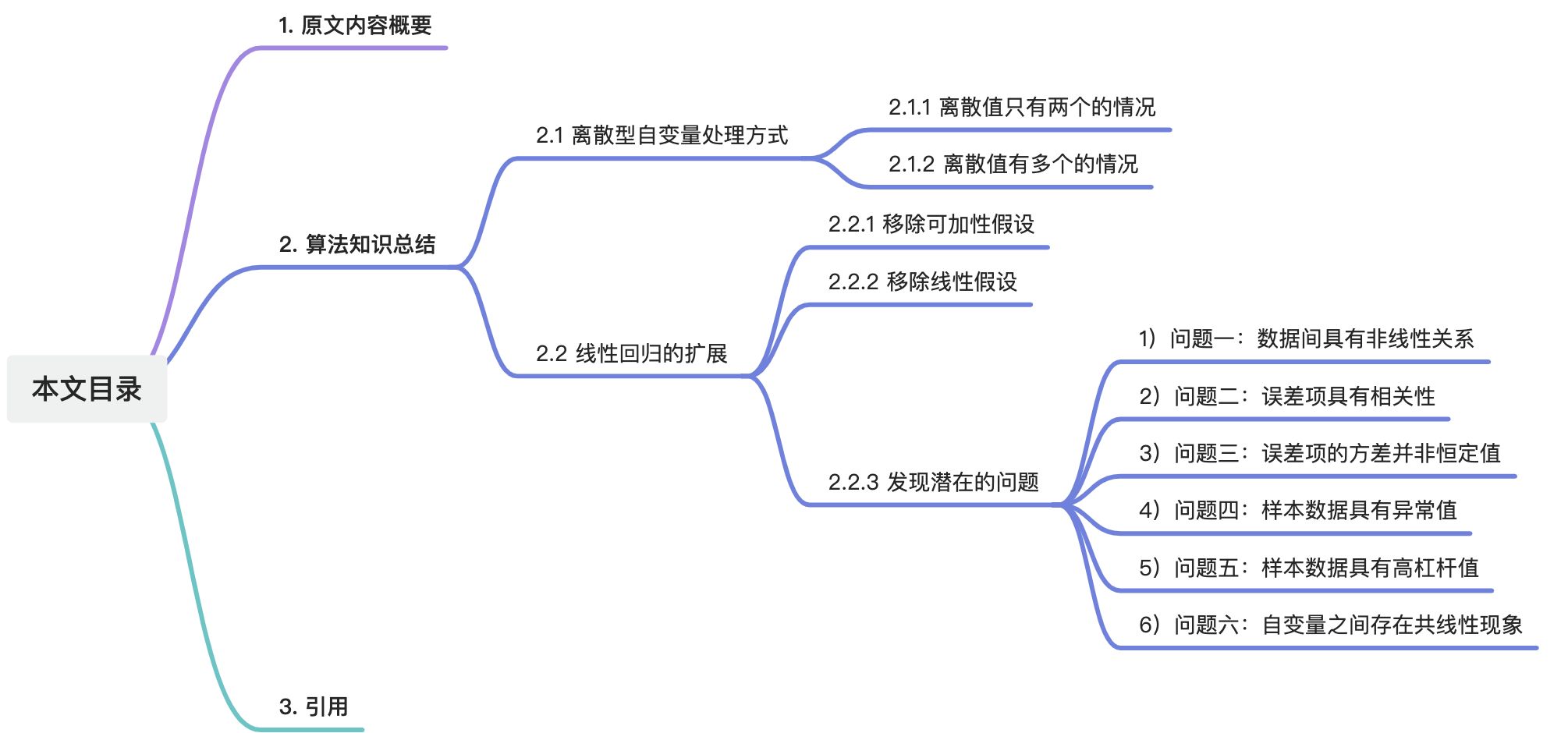
这里写目录标题
1. 原文内容概要
由于书中第三章的内容较多,故读书笔记分为【上】【下】两节分别输出。
本次笔记承接之前【上】节的内容,继续为大家解析第三章——线性回归(Linear Regression)的内容。本次笔记主要包括第三章中作者对于线性回归的一些深度思考(扩展和优化),读完之后大家对于线性回归一定会有更深的认识。
2. 算法知识总结
2.1 离散型自变量处理方式
离散型变量(英文一般会说成,categorical variable、qualitative variable等)是跟连续型变量(quantitative variable)相对应的概念,简单理解就是离散型变量的离散值是动态可枚举的。在处理线性回归模型中的离散型变量时,应根据离散值的枚举个数进行分类处理。通常情况下,我们将离散值个数等于2的情况视为一种特殊情况,而将离散值个数大于2的情况视为另一种情况。
2.1.1 离散值只有两个的情况
这种情况最简单,直接用哑谜变量(dummy variable)。比如性别这个变量,在训练样本中的值可能显示的是“男”和“女”,在代入线性模型前,需要将其转换成哑谜变量,即“0”(表示男)和“1”(表示女)。这种将离散变量转化成二进制表示的方式,在机器学习领域叫做独热编码(one-hot encoding)。
作者举了一个信贷的实际例子,在信贷的实验数据(credit data set)中,有一个离散变量叫“是否拥有房产”,离散值为“是”和“否”,作者用这个变量来预测一个人的信用卡贷款余额(credit card balance)。作者在代入模型前将其转变为哑谜变量(“0”表示没有房产,“1”表示有房产):
将变换得到的哑谜变量代入线性模型,表示形式如下所示:
在上面的公式中, β 0 β_0 β0表示那些没有房产的人平均的贷款余额, β 0 + β 1 β_0+β_1 β0+β1表示那些有房产的人平均的贷款余额, β 1 β_1 β1表示有房产的人和没房产的人在贷款余额上的平均差异。用信贷数据拟合后,模型参数结果如下所示:
相信大家通过上一节读书笔记的学习,对这些参数的解读应该不在话下了吧~
值得注意的是,我们这里将“是否拥有房产”这个变量的值转变成“0”和“1”不是必须的,我们可以转换成任何其他的枚举值,比如“-1”代表没有房产,“1”代表有房产。只是在最终模型解释方面存在一些差异,但预测结果的数值将保持不变。
就拿“-1”代表没有房产,“1”代表有房产举例,线性模型的变成了如下形式:
系数的解释也变成: β 0 β_0 β0表示整体的平均贷款余额(有房产者的平均贷款余额和无房产者的平均贷款余额之和的一半); β 1 β_1 β1表示有房产者与无房产者在贷款余额上与整体平均贷款余额的绝对差距。在这个例子中, β 0 β_0 β0最终拟合的值为 519.665 519.665 519.665(它其实是有房者的平均贷款余额 529.53 529.53 529.53与无房者的平均贷款余额 509.80 509.80 509.80两者的均值,大家自己思考下 529.53 529.53 529.53和 509.80 509.80 509.80是哪里得到的), β 1 β_1 β1为 9.865 9.865 9.865(它其实是 19.73 19.73 19.73的一半,大家找找哪里出现过 19.73 19.73 19.73)。
2.1.2 离散值有多个的情况
上面讲的都是离散值只有2个的情况,那如果一个离线变量的离散值个数大于2个该如何应对呢?比如信贷数据集中,有个叫**“地区”(region)的离散变量,一共有3个枚举值,即“东”(east)、“南”(south)和“西”(west)**。可能大家最直观的反应就是,用“1”、“2”、“3”分别表示“东”、“南”、“西”。这样做是有问题的,因为当我们用“1”、“2”、“3”这仨有序数字来表示方位时,会给模型一个错误的指引,让模型认为“西”最大,“东”最小,“南”在中间,并且“东”比“南”就少1个单位。很显然,这看起来是很荒谬的。
我们可以用多个哑谜变量来解决上面的问题。比如用两个哑谜变量,其中 x 1 x_{1} x1表示这个人是否来自南方(“1”表示来自南方,“0”表示不来自南方), x 2 x_{2} x2表示这个人是否来自西方(“1”表示来自西方,“0”表示不来自西方)。大家注意下,对于枚举值只有3个的离散型变量,我们一般只用2个哑谜变量就能完整表达了。比如上面我们用两个哑谜变量表示了是自“南”方和“西”方的信息,那来自“东”方的信息怎么表示呢?答案就是,不含有这两个哑谜变量的模型,就表示了来自“东”方的信息。我们把这个“不含有哑谜变量的模型”叫做基准模型(baseline)(The level with no dummy variable—East in this example—is known as the baseline)。值得注意的是,这个“基准”的选择是完全随机的,随你的心情,比如这个例子中,你完全可以选择“南”方作为“基准”。


具体来说, β 0 β_0 β0表示东区人的平均贷款余额, β 1 β_1 β1表示南区人与东区人在平均贷款余额上的差距, β 2 β_2 β2表示西区人与东区人在平均贷款余额上的差距。下面是拟合的具体结果:
2.2 线性回归的扩展
标准的线性模型需要满足很多“苛刻”的前提,其中最重要的是可加性和线性关系。
(Two of the most important assumptions state that the relationship between the predictors an








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








