秋招算法总结：线段树_树状数组_原理_区别_代码实现

本文链接：https://blog.csdn.net/weixin_41944387/article/details/125479822

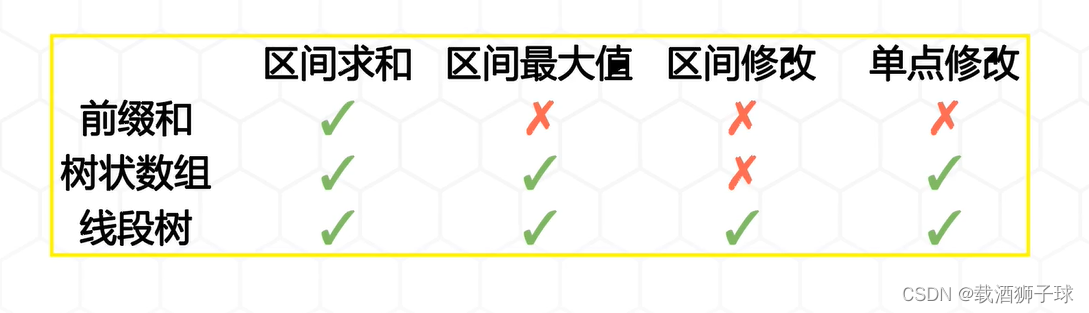
0 线段树与树状数组的区别

线段树和树状数组都需要满足区间的结合律和可加性：
- 比如加法，乘法，最大值，最小值
树状数组只能维护前缀“操作和”(前缀和，前缀积，前缀最大最小)，而线段树可以维护区间操作和
树状数组的区间操作是利用两个前缀和操作抵消的（操作存在逆元的情况下）
- 维护区间和，模质数意义下的区间乘积，区间 xor 和。能这样做的本质是取右端点的前缀结果，然后对左端点左边的前缀结果的逆元做一次操作，所以树状数组的区间询问其实是在两次前缀和询问
- 但维护不了另一些的:最大/最小值，模非质数意义下的乘法，原因在于这些操作不存在逆元，所以就没法用两个前缀和做。

请添加图片描述

1 树状数组

1.1 核心思想

⁉️如何基于编号，构件一个不重叠的子序列集合。

假如需要求前13个元素的前缀和 $num=13=1101_2$ ：

首先处理 $bi t = 1$ 这一位，其代表的范围是：
$1100_2~+0001_2~,~1100_2~+~0001_2]$
然后在num上减去他： $num−=(1<<(bit−1))=1100_2$

然后，我们处理 $bi t = 3$ 这一位：其代表的范围是：
$1000_2~+~0001_2~,~1000_2~+~0100_2]$
同样，我们在num上减去它

最后我们处理 $bi t = 4$ 这一位：其代表的范围是：
$0000_2~+~0001_2~,~0000_2~+~1000_2]$
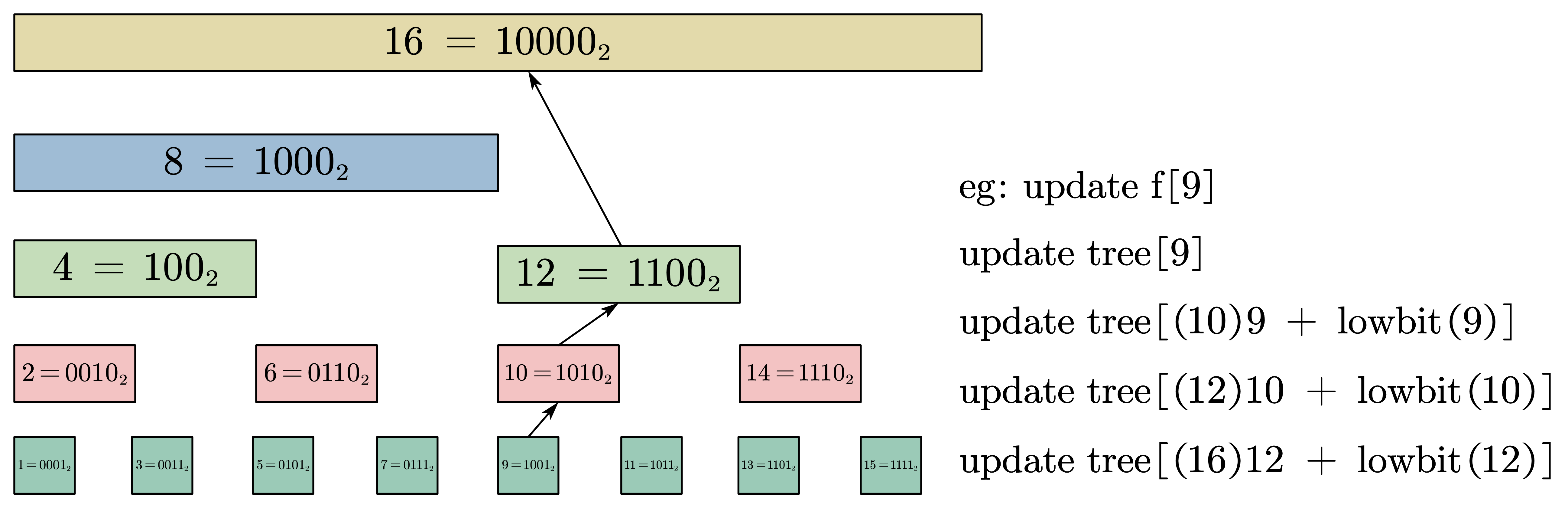
我们回顾整个处理流程，可以惊讶的发现，❤️如果我们按照逆序处理，我们每次处理的bit都是当前编号的最后的为1位。
$[c u r - l o w bi t (c u r) + 1, c u r]$
我们将每次处理的bit定义为 lowbit, lowbit(i)即i这个数的最低位是第几位（从右数从1开始）

$t ree [i]$ 控制
$[i - l o w bi t (i) + 1, i]$
范围内的f[i]

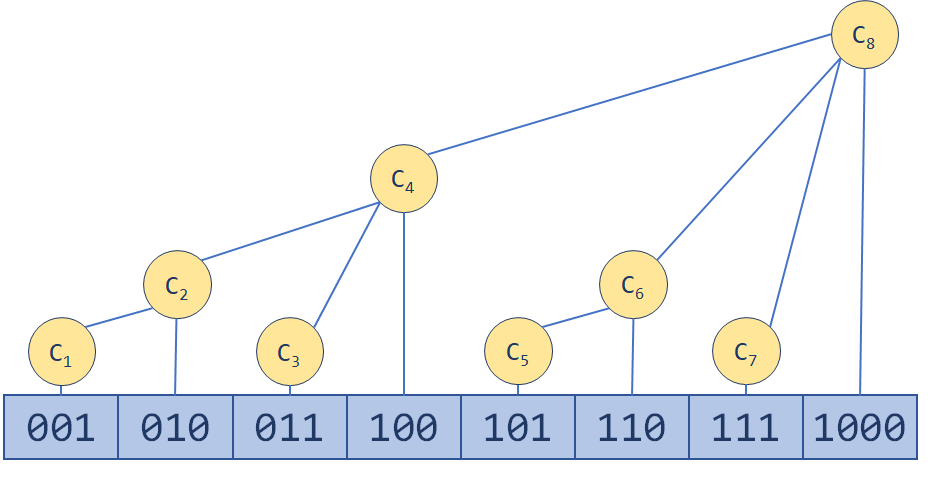
😍总结

树状数组，将对前 $n$ 个元素求和分为了 $log_2n$ 个不重叠的部分，下图中格内数字代表 $t ree [i]$

1.2 流程伪码

求和

 T tree[maxn];
template <typename T>
T query(int i){
	T res = 0;
    while (i > 0){
        res += tree[i];
        i -= lowbit(i);
    }
    return res;
}

更新

int n; // BIT 的大小， BIT index 从 1 开始
T tree[maxn];
template <typename T>
void add(int i, T x){
    while (i <= n){
        tree[i] += x;
        i += lowbit(i);
    }
}

lowbit运算
$lowbit(x)=(~x~\&~(−x))$
建树

for (i = 1; i <= n; ++i){
    scanf("%d", arr + i), update(i, arr[i], c, n);
}

🤡注意

BIT是从下标1开始存储的

1.3 例题

307. 区域和检索 - 数组可修改 - 力扣（LeetCode）

2 线段树

2.1 原理

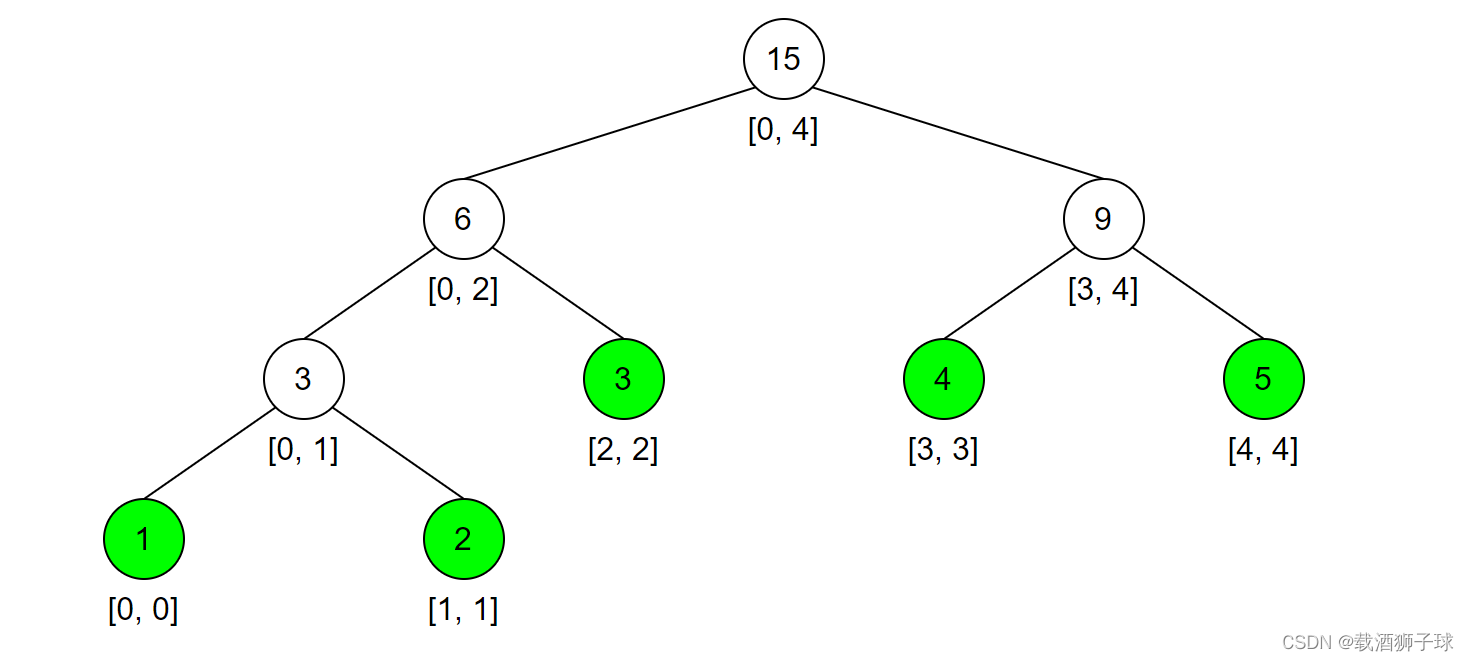
❓二叉搜索树如何编号

二叉搜索树的根节点编号为1，对于每个节点，假如其编号为N，它的左儿子编号为2N，右儿子编号为2N+1。因此，整个二叉搜索树的编号如下

线段树本质也是一个❤️二叉搜索树，区别在于线段树的❤️每一个节点记录的都是一个区间，每个区间都被平均分为2个子区间，作为它的左右儿子。比如说区间[1，10]，被分为区间[1，5]作为左儿子，区间[6，10]作为右儿子。❤️当一个区间的左右边界已经相等时，比如[1，1]，表示这个区间内只有一个元素了，此时不能再分割，因此它就没有左右儿子节点了

在这里插入图片描述

⁉️节点代表区间的范围与节点编号关系

节点 $p$ 储存区间 $[l, r]$ 的和，设
$mid=\lfloor\frac{l+r}{2}\rfloor$
左子树 $2 p$ 存储区间为 $[l, mi d]$ , 右子树 $2 p + 1$ 存储区间为 $[mi d + 1, r]$

左节点对应的区间长度，与右节点相同或者比之恰好多1。

⁉️区间修改的懒标记

❤️任何区间都是线段树上某些节点的并集，要修改的区间与当前区间存在三种关系：

要修改区间与当前区间相交为空集
要修改的区间被当前区间拆开
要修改的区间包含在当前区间的左孩子或右孩子内

懒惰标记的初衷就是延迟修改，❤️找到目标区间后直接在相应节点打上懒标记，不需要再向下递归

现在假如我们需要把区间[5，7]每个元素增加2：

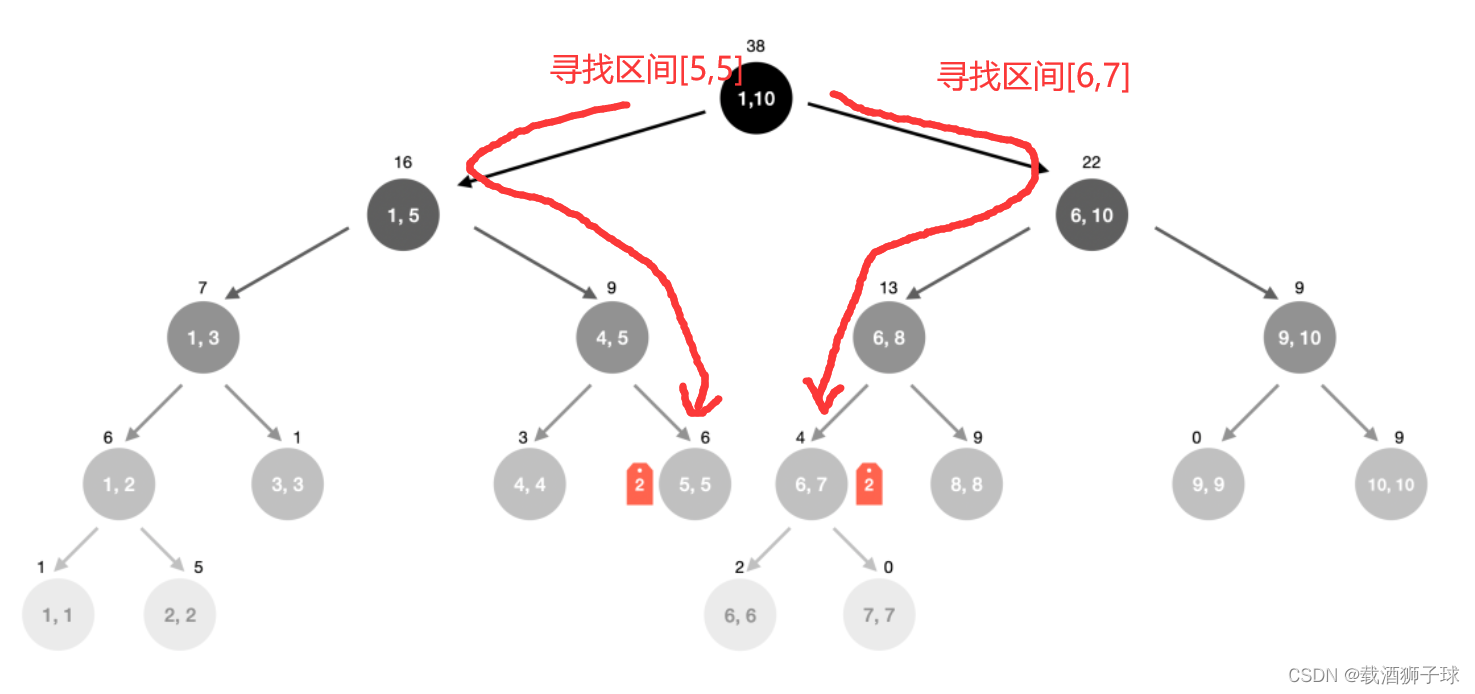
请添加图片描述

🤡注意

找到目标区间后要做两件事：

❤️更新当前节点代表区间的区间和
打上懒标记

区间和增加的值要乘区间长度，但懒惰标记的值不用乘，所以懒标记其实是

❤️延迟下放+只下放一层

⁉️pushdown函数

下传懒惰标记步骤有3步：

将懒惰标记传递给儿子
更新儿子的值
清空当前节点的懒惰标记
叶子节点不用下传懒惰标记

这个过程并不是递归的，我们只往下传递一层，以后要用再才继续传递。

2.2 指针实现

线段树建立

请添加图片描述

2.3 数组实现

线段树建立

// 参数：当前操作左区间，当前操作右区间，当前操作树的节点编号
void build(ll l = 1, ll r = n, ll p = 1)
{
    if (l == r) // 到达叶子节点
        tree[p] = A[l]; // 用数组中的数据赋值
    	//到达叶子节点时，左右区间相等，等于要新建的数在原始数组中的下标
    else
    {
        ll mid = (l + r) / 2;
        build(l, mid, p * 2); // 先建立左子树
        build(mid + 1, r, p * 2 + 1);// 建立右子树
        tree[p] = tree[p * 2] + tree[p * 2 + 1]; // 该节点的值等于左右子节点之和
    }
}

也可以把参数中当前操作区间的区间端点信息、和存储到struct Node里，就不用以参数传递了

区间修改

void modifySegment(int l, int r, int value, int num) { // [l,r]每一项都增加value
    if (tree[num].l == l && tree[num].r == r) { // 找到当前区间
        tree[num].sum += ( r - l + 1 ) * value; // r-l+1是区间元素个数
        tree[num].lazy += value;
        return;
    }
    int mid = (tree[num].l + tree[num].r) / 2;
    if (r <= mid) { // 在左区间
        modifySegment(l, r, value, num * 2);
    }
    else if (l > mid) { // 在右区间
        modifySegment(l, r, value, num * 2 + 1);
    }
    else { // 分成2块
        modifySegment(l, mid, value, num * 2);
        modifySegment(mid + 1, r, value, num * 2 + 1);
    }
    tree[num].sum = tree[num * 2].sum + tree[num * 2 + 1].sum;
}

区间查询

pushdown函数

void pushdown (int num) {
    if(tree[num].l == tree[num].r) { // 叶节点不用下传标记
        tree[num].lazy = 0; // 清空当前标记
        return;
    }
    
    tree[num * 2].lazy += tree[num].lazy; // 下传左儿子的懒惰标记
    tree[num * 2 + 1].lazy += tree[num].lazy; // 下传右儿子的懒惰标记
    
    tree[num * 2].sum += (tree[num * 2].r - tree[num * 2].l + 1) * tree[num].lazy; // 更新左儿子的值
    tree[num * 2 + 1].sum += (tree[num * 2 + 1].r - tree[num * 2 + 1].l + 1) * tree[num].lazy; // 更新右儿子的值
    
    tree[num].lazy=0; // 清空当前节点的懒惰标记
}

查询

int query (int l, int r, int num) {
    if (tree[num].lazy != 0) { // 下传懒惰标记
        pushdown(num);
    }
    if (tree[num].l == l && tree[num].r == r) { // 找到当前区间
        return tree[num].sum;
    }
    int mid = (tree[num].l + tree[num].r) / 2;
    if (r <= mid) { // 在左区间
        return query(l, r, num * 2);
    }
    if (l > mid) { // 在右区间
        return query(l, r, num * 2 + 1);
    }
    return query(l, mid, num * 2) + query(mid + 1, r, num * 2 + 1); // 分成2块
}