树状数组（尽量详细了）

树状数组

树状数组是一个查询和修改复杂度都为log(n)的数据结构。主要用于数组快速单点修改，和快速区间求和.

引子

不结合示例分析的题解都是流氓，这里给出leetcode上的一道问题来说明树状数组的特点和优势

Loading Question... - 力扣（LeetCode） (leetcode-cn.com)

简单描述就是，对于一个给定的数组A，希望能够设计一个update函数来修改其中一个数的值，然后再设计一个sum函数来计算数组下标再给定参数l和r之间的值之和。关键点在于这两个函数可能被无数次调用，所以需要保证两个函数的复杂度都要小。

暴力算法（不佳）

update函数采用对数组直接修改的方法。

对于sum函数，采用暴力算法。就是对于用例中的每一个l和r，都将它们之间的所有数求和。但是这道题的操作数很大，会超时。

前缀和算法（不佳）

sum函数，考虑前缀和的方法，也就是采用动态规划的方法，设计一个新的数组pre来表示前缀和。

其基本思想为，pre[i]表示A[0]+A[1]+A[2]+...+A[i-1]+A[i]。具体操作的时候我们只需要设置pre[i] = pre[i-1]+A[i]即可。

然后如果希望计算数组下标l到r的区间和，只需要计算pre[r]-pre[l-1]即可。希望使用这种方式达到简化计算复杂度的目的。

但是这时候考虑update函数，当我们对数组A直接进行修改值之后，我们发现pre数组也需要对应进行修改，下面通过示例进行说明：

原数组：A= {1,2,3,4,5}

前缀和数组：pre = {1,3,6,10,15}

分析：当我们对A[3]修改，将其原值3改为2的时候。

考虑到pre数组是由A数组得到的,因为

pre[0] = A[0]

pre[1] = A[0]+A[1]

pre[2] = A[0]+A[1]+A[2]

pre[3] = A[0]+A[1]+A[2]+A[3]

pre[4] = A[0]+A[1]+A[2]+A[3]+A[4]

我们会发现，A[3]的修改会影响到pre[3]和pre[4]，所以我们需要对pre[3]和pre[4]都进行修改

pre[3]新值 = A[0]+A[1]+A[2]+A[3]新值

pre[4]新值 = A[0]+A[1]+A[2]+A[3]新值+A[4]

综上，归纳可以得知，如果修改了A[i]的值，对于所有j>=i, pre[j]的值都需要改变，具体改变量为pre[j] = pre[j] + A[i]新值 -A[i]原值

这样一来，对于update函数，我们的复杂度就会提高，可以认为是O(n)，即使当前sum函数复杂度变为了O(1)，这道题总的复杂度依然是O(1)。

痛点

针对上述问题我们发现，需要做到两点：

首先需要能够快速计算区间和，其次要保证在修改了数组的值之后，对相关数据结构内容修改的操作数也要尽量少

这里总结上述分析，我们知道，希望能够设计新的数据结构，让它能够同时包含多个节点信息，类似pre数组，这样计算区间和就能够提速。然后希望这个数据结构的更新也要尽量快。这里就引入了树状数组的概念。

树状数组

二叉树大家一定都知道，如下图

 

如果每个父亲都存的是两个儿子的值，是不是就可以解决这类区间问题了呢。是的没错，但是这样的树形结构，叫做线段树。

那真的的树形结构是怎样的，和上图类似，但省去了一些节点，以达到用数组建树。

对于一般的二叉树,我们是这样画的

 

把位置稍微移动一下,便是树状数组的画法，最下面一行为原数组

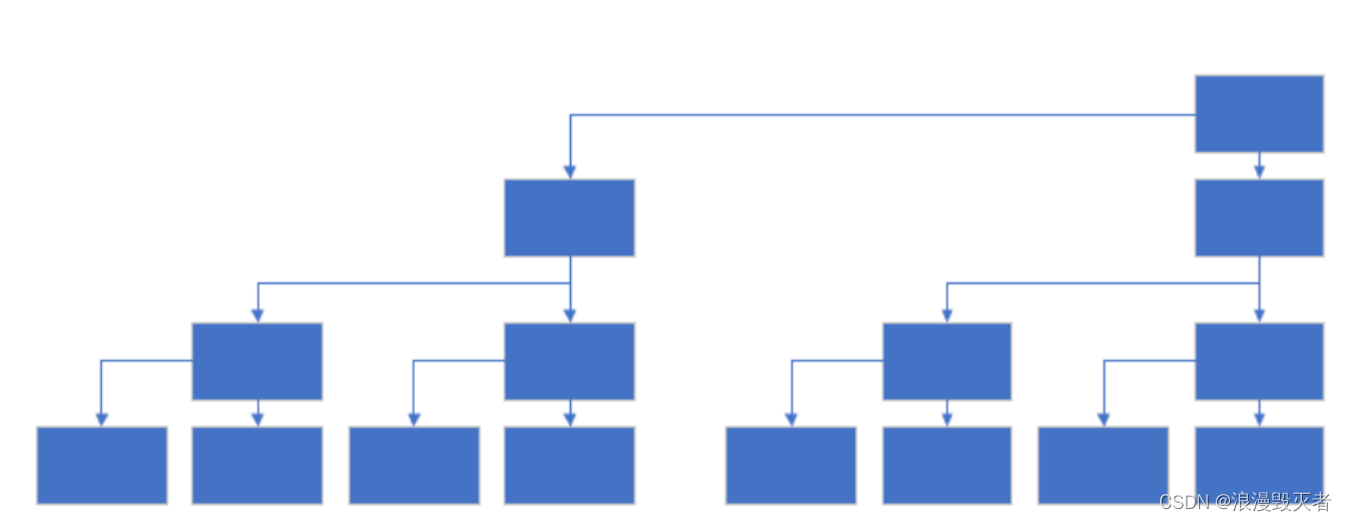
需要注意的是，图中的子节点包括自己，比如说8这个节点，里面的值是原始数组中[5，6，7，8]的和

这里首先我们将原数组称为A数组，树状数组称为C数组

需要设计两个过程，更新过程和查询过程

这两个过程就是树状数组的最核心应用，对应快速修改节点值，快速计算前缀和两个功能

参考下图

 

最底下一行黑色节点从左到右为原数组A,而带有数字的红色节点就是树状数组C的节点

我们可以看到比如说C8节点，它的子节点有C4，C6，C7，A8(第八个黑色节点)而C4，C6，C7由分别有自己的子节点。

根据这张图，对于8节点可以表示成：

C[8] = C[4] + C[6] +C[7] +A[8]

换一张图来理解一下：

 

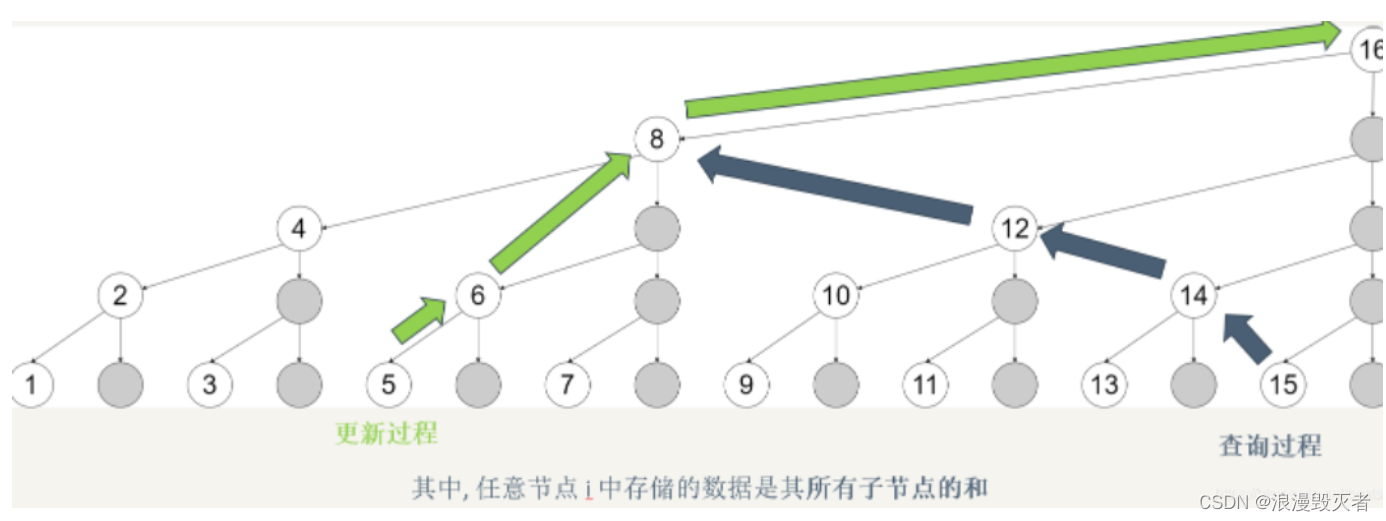
这张图里面表示的所有数字节点就是树状数组C，最下面一行从左到右同时也表示原数组A（包括灰色节点）。图中标出了修改节点5需要修改的所有节点值的更新过程和计算下标0~15的节点值之和的查询过程。

更新过程

根据上面树状数组的计算，我们参考这张图能够知道，C5是C6的子节点，而C6是C8的子节点，当我们修改A5的时候

因为C5 = A5，所以C5会变化，导致C6变化，再导致C8变化，那么变化的值为多少呢，均为 A5新值减去A5旧值

这里的思想和之前提到的前缀和有点相似，前缀和中是将pre5及后面所有的节点都要修改(因为这些节点都包含了5节点的信息)，但是这里只需要修改C5，C6和C8节点的信息（因为只有这几个节点包含了5节点的信息），总体来说比起前缀和方法更新节点的时候对数据结构的更新就很快了

下面有人会问，你这是画图看出来要更新C5，C6和C8。那么具体是修改了哪些节点呢？这里我们要从二进制的角度来看，重新画一张二进制的图，将所有节点上的十进制改为了二进制表示：

 

对应过来，我们会发现C101的值变化后，会影响C110，进而影响C1000的值

那么101和110和1000之间有什么关系呢？

可以归纳得出，110是由101加上1得到，1000是由110加上10得到

101加1是因为101中只保留最低位的1就是1， 而110加10是因为110中只保留最低位1是10

所以我们只需要算出当前节点下标二进制表示的最低位1的位置，然后算出只保留这个1得到的数，结合当前节点的下标，就可以计算出下一个需要修改的节点的下标了

这里我们设计一个函数lowbit(int x)用于计算给定一个下标x，返回：其二进制下标只保留最低位1会得到的那个数

//借鉴前人智慧，可以轻松得到
int lowbit(x){return x&(-x);}

简单解释一下为什么可以通过x&(-x)得到这个数

我们知道,对于一个数的负数就等于对这个数取反+1

以二进制数11010为例:11010的补码为00101,加1后为00110,两者相与便是最低位的1

其实很好理解,补码和原码必然相反,所以原码有0的部位补码全是1,补码再+1之后由于进位那么最末尾的1和原码

最右边的1一定是同一个位置(当遇到第一个1的时候补码此位为0,由于前面会进一位,所以此位会变为1)

所以我们只需要进行a&(-a)就可以取出最低位的1了

那么在A101(C101)的值变了之后，我们只需要对101计算lowbit得到1，然后修改C110的值，然后计算110的lowbit得到10，再修改C1000的值，这样不断反复，直到当前需要修改的节点下标越界即可。这样我们就得到了我们的add函数：

//tr表示树状节点
/**
* 用于进行树状数组的更新过程
* @param x: 被修改的数组下标
* @param val: 修改量（负数代表减少）
*/
public void add(int x,int val){
        for(int i=x;i<=n;i+=lowbit(i)){
            tr[i] += val;
        }
    }

整个复杂度为O(logn),因为每次lowbit导致移了一位，相当于反复对数组长度n除以2直到0的复杂度。

查询过程

 

查询过程是计算从A[0]到A[i]的所有值进行求和

如果我需要查询A[0]~A[15]之和,观察当前图我们会发现

8节点包含了1~8，12节点包含了9~12，14节点包含了13~14，15节点包含了15

那我们只需要将C8,C12,C14,C15进行求和即可

但是问题又来了，这是画图发现的，具体操作的时候需要对哪几个C进行求和呢？

同样的我们将其转换为二进制表示的图：

 

首先对sum置零。

归纳可得，对于15的二进制节点1111，我们减去1111保留最低位1的数1，得到1110.然后让sum加上节点1110的值。

然后对于1110，同样减去其保留最低位1的数10得到1100，然后让sum加上节点1100的值。

再对于1100，减去其保留最低位1的数100得到1000，然后让sum加上节点1000的值。

再对于1000，减去其保留最低位1的数1000得到0。这时不能再算了，因为已经到头了。

所以我们可以发现，又需要用到lowbit这个函数了。基于上述思想，整个计算前缀和流程可以表示如下：

//tr表示树状节点
/**
* 用于进行前缀求和的查询过程
* @param x: 需要查询的数组下标x
* @return 计算从0节点到x节点之间所有值之和
*/
public int pre_sum(int x){
        int sum = 0;
        for(int i=x;i>0;i-=lowbit(i)){
            sum += tr[i];
        }
        return sum;
    }

查询过程相当于是求前缀和的过程，那么有了前缀和，我们就可以通过前缀和的作差得到其中部分区间和的答案了。

这里使用到的复杂度为O(logn)，因为每次lowbit移了一位，相当于反复对数组长度n除以2直到0的复杂度。

代码参考

至此，所有的细节就完成了，下面给出针对leetcode上问题的具体题解

307. 区域和检索 - 数组可修改 - 力扣（LeetCode） (leetcode-cn.com)

class NumArray {
    private int[] tr;
    private int n;
    private int[] nums;
    public NumArray(int[] nums) {
        this.n = nums.length;
        this.tr = new int[n+1]; //注意，下标0的值设置为默认的0，是为了处理的方便
        this.nums = nums;
        //初始化，其实就是利用add函数，在数组默认0的基础上进行初次修改
        for(int i=0;i<n;i++){
            add(i+1,nums[i]);
        }
    }
    
    public void update(int index, int val) {
        add(index+1,val-nums[index]);
        this.nums[index] = val;
    }
    
    public int sumRange(int left, int right) {
        return pre_sum(right+1)-pre_sum(left);
    }
​
    public int lowbit(int x){
        return x&(-x);
    }
​
    public int pre_sum(int x){
        int sum = 0;
        for(int i=x;i>0;i-=lowbit(i)){
            sum += tr[i];
        }
        return sum;
    }
​
    public void add(int x,int val){
        for(int i=x;i<=n;i+=lowbit(i)){
            tr[i] += val;
        }
    }
}

模板

这里参考了三叶姐的树状数组的模板,还请大家多多去给她捧场

class NumArray {
    int[] tree;
    int lowbit(int x) {
        return x & -x;
    }
    int query(int x) {
        int ans = 0;
        for (int i = x; i > 0; i -= lowbit(i)) ans += tree[i];
        return ans;
    }
    void add(int x, int u) {
        for (int i = x; i <= n; i += lowbit(i)) tree[i] += u;
    }
    int[] nums;
    int n;
    public NumArray(int[] _nums) {
        nums = _nums;
        n = nums.length;
        tree = new int[n + 1];
        for (int i = 0; i < n; i++) add(i + 1, nums[i]);
    }
    public void update(int i, int val) {
        add(i + 1, val - nums[i]);
        nums[i] = val;
    }
    public int sumRange(int l, int r) {
        return query(r + 1) - query(l);
    }
}

参考博客

(72条消息) 树状数组 数据结构详解与模板(可能是最详细的了)bestsort的博客-CSDN博客树状数组

我喜欢你啊。 (cnblogs.com)