C语言实现统计一棵二叉树的所有双分支结点算法

（一）第一种方法：

》》 算法思想：

（二）第二种方法

》》两种方法的完整代码编写：

#include<stdio.h>
#include<stdlib.h>
#include<iostream>
using namespace std;

typedef int ElemType;
typedef struct BiNode {
	ElemType data;
	BiNode* lchild;
	BiNode* rchild;
}BiNode, * BiTree;

//构建二叉树
BiNode* Create(BiNode* bt) {
	static int i = 0;
	char ch;
	//string str = "AB#D##C##";
	//string str = "124##56##7##3##";
	//string str = "ABD#G##E##CF###";
	string str = "ABD#GH##I##E##CF###";
	ch = str[i++];
	if (ch == '#')bt = NULL;//建立一棵空树 
	else {
		bt = (BiTree)malloc(sizeof(BiNode)); bt->data = ch;//生成一个结点，数据域为ch
		bt->lchild = Create(bt->lchild);//递归建立左子树
		bt->rchild = Create(bt->rchild);//递归建立右子树
	}
	return bt;
}

//本题也可以设置一个全局变量的cnt,每遍历到一个结点时，判断每个结点
//是否为分支结点（左、右结点都不为空，注意是双分支），若是则cnt++;
void visit(BiTree T,int& cnt) {
	if (T->lchild != NULL && T->rchild != NULL)
		cnt++;
	printf("%c ", T->data);
}

void CntInOrder(BiTree T, int& cnt) {
	if (T != NULL) {
		CntInOrder(T->lchild,cnt);//递归遍历左子树
		visit(T,cnt);//访问根结点
		CntInOrder(T->rchild, cnt);//递归遍历右子树
	}
}

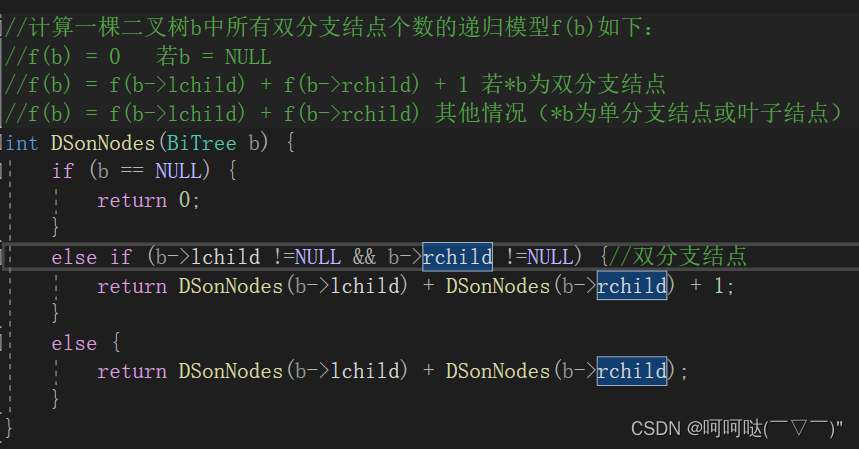
//计算一棵二叉树b中所有双分支结点个数的递归模型f(b)如下：
//f(b) = 0   若b = NULL
//f(b) = f(b->lchild) + f(b->rchild) + 1 若*b为双分支结点
//f(b) = f(b->lchild) + f(b->rchild) 其他情况（*b为单分支结点或叶子结点）
int DSonNodes(BiTree b) {
	if (b == NULL) {
		return 0;
	}
	else if (b->lchild !=NULL && b->rchild !=NULL) {//双分支结点
		return DSonNodes(b->lchild) + DSonNodes(b->rchild) + 1;
	}
	else {
		return DSonNodes(b->lchild) + DSonNodes(b->rchild);
	}
}

int main() {
	BiTree T = (BiTree)malloc(sizeof(BiNode));
	T = Create(T);
	//第一种方法：对二叉树进行中序遍历统计出的所有双分支结点个数
	int cnt = 0;
	CntInOrder(T, cnt);
	printf("\n对二叉树进行中序遍历统计出的所有双分支结点个数为：%d",cnt);

	//第二种方法：设计一棵二叉树b中所有双分支结点个数的递归模型f(b)
	cnt = DSonNodes(T);
	printf("\n设计一棵二叉树b中所有双分支结点个数的递归模型f(b)：%d",cnt);
}

 、