【椭球大地测量学】Python及MATLAB实现贝塞尔大地问题正反解计算编程（含流程图）

---

一、功能

使用Python实现贝塞尔大地问题正反解计算，使用CGCS2000国家大地坐标系的椭球数据。
功能为：
①已知椭球面上某一已知点的大地坐标（L1，B1）以及该已知点至未知点的大地线长(S12)和大地方位角（A1），求未知点大地坐标（L2，B2）和大地方位角（A2）
②已知椭球面上两已知点的大地坐标（L1，B1，L2，B2），求该两点间的大地线长(S12)和正反大地方位角（A1，A2）

---

二、使用方法

将文件计算程序与接口程序放在同一文件夹下，双击即可运行接口程序。
（注：该程序包含计算程序和接口程序，用户可以通过调整接口程序创建属于自己的交互界面。流程图在下载的压缩文件中。）

---

三、算法流程图

（1）贝塞尔大地问题正算

（2）贝塞尔大地问题反算

---

四、Python程序

（1）计算程序

import math as m


class Earth():
    # 建立椭球类，采用SGCS2000中国大地坐标系数据
    def __init__(self):  # 给定椭球数据
        # 长半轴
        self.a = 6378137.0
        # 短半轴
        self.b = 6356752.31414
        # 扁率
        self.f = 1/298.257222101
        # 第一偏心率的平方
        self.e1s = m.pow(0.0818191910428, 2)
        # 第二偏心率的平方
        self.e2s = self.e1s / (1 - self.e1s)

    def W(self, B):  # 计算第一辅助函数
        self.w = m.sqrt(1 - self.e1s * m.sin(B) * m.sin(B))
        return self.w

    def V(self, B):  # 计算第二辅助函数
        self.v = m.sqrt(1 + self.e2s * m.cos(B) * m.cos(B))
        return self.v


class Bessel():
    # 建立贝塞尔解算类
    def __init__(self):  # 导入椭球数据
        self.E = Earth()

    def Direct(self, L1, B1, A1, S, T):  # 正算
        # 标记精度：高于米级为1，米级为2，低于百米级为3
        self.Type = {1: (1, 1), 2: (0, 1), 3: (0, 0)}
        self.t1 = self.Type[T][0]
        self.t2 = self.Type[T][1]

        # 将角度转化为弧度
        self.L1, self.B1, self.A1 = m.radians(L1), m.radians(B1), m.radians(A1)

        # Ⅰ将椭球面元素投影到球面上
        # 由B1求u1
        self.u1 = m.atan(m.sqrt(1 - self.E.e1s) * m.tan(self.B1))
        # 计算辅助函数值
        self.M = m.atan(m.tan(self.u1) / m.cos(self.A1))
        if self.M < 0:
            self.M += m.pi
        self.m = m.asin(m.cos(self.u1) * m.sin(self.A1))
        if self.m < 0:
            self.m += 2 * m.pi

        # 将S化为σ
        self.k2 = self.E.e2s * m.cos(self.m) * m.cos(self.m)
        self.k4 = self.k2 * self.k2
        self.k6 = self.k4 * self.k2 * self.t1
        self.ρ = 180 / m.pi * 3600
        self.α1 = m.sqrt(1 + self.E.e2s) / self.E.a * (1 - self.k2 / 4 + 7 / 64 * self.k4 - 15 / 256 * self.k6)
        self.β1 = self.k2 / 4 - self.k4 / 8 + 37 / 512 * self.k6
        self.γ1 = (self.k4 - self.k6) / 128 * self.t2
        self.σ1 = self.α1 * S
        while True:
            self.σ2 = self.α1 * S + self.β1 * m.sin(self.σ1) * m.cos(2 * self.M + self.σ1) + \
                self.γ1 * m.sin(2 * self.σ1) * m.cos(4 * self.M + 2 * self.σ1)
            if abs(self.σ1 - self.σ2) < 0.1 / self.ρ / 3600:
                break
            self.σ1 = self.σ2
        self.σ = self.σ2

        # Ⅱ在球面上解算
        # 求A2
        self.A2 = m.atan(m.tan(self.m) / m.cos(self.M + self.σ))
        if self.A2 < 0:
            self.A2 += m.pi
        if self.A1 < m.pi:
            self.A2 += m.pi
        # 求u2
        self.u2 = m.atan(-m.cos(self.A2) * m.tan(self.M + self.σ))
        # 求λ
        self.λ1 = m.atan(m.sin(self.u1) * m.tan(self.A1))
        if self.λ1 < 0:
            self.λ1 += m.pi
        if self.m > m.pi:
            self.λ1 += m.pi
        self.λ2 = m.atan(m.sin(self.u2) * m.tan(self.A2))
        if self.λ2 < 0:
            self.λ2 += m.pi
        if self.m < m.pi:
            if self.M + self.σ > m.pi:
                self.λ2 += m.pi
        else:
            if self.M + self.σ < m.pi:
                self.λ2 += m.pi
        self.λ = self.λ2 - self.λ1

        # Ⅲ将球面元素换算到椭球面上
        # 由u2求B2
        self.B2 = m.atan(m.sqrt(1 + self.E.e2s) * m.tan(self.u2))
        # 求L2
        self.α2 = (0.5 + self.E.e1s / 8 - self.E.e1s * self.E.e1s / 16) * self.E.e1s - \
            self.t1 * (self.E.e1s / 16 * (1 + self.E.e1s) * self.k2 - 3 / 128 * self.E.e1s * self.k4)
        self.β2 = self.t2 * (self.E.e1s / 16 * (1 + self.t1 * self.E.e1s) * self.k2 -
                             self.t1 * self.E.e1s / 32 * self.k4)
        self.γ2 = self.t2 * self.E.e1s / 256 * self.k4
        self.L2 = self.L1 + self.λ - m.sin(self.m) * (self.α2 * self.σ + self.β2 * m.sin(self.σ)
                                                      * m.cos(2 * self.M + self.σ) + self.γ2
                                                      * m.sin(2 * self.σ) * m.cos(4 * self.M + 2 * self.σ))

        self.result = [self.L2 * 180 / m.pi, self.B2 * 180 / m.pi, self.A2 * 180 / m.pi]
        return(self.result)

    def Inverse(self, L1, B1, L2, B2, T):  # 反算
        # 标记精度：高于米级为1，米级为2，低于百米级为3
        self.Type = {1: (1, 1), 2: (0, 1), 3: (0, 0)}
        self.t1 = self.Type[T][0]
        self.t2 = self.Type[T][1]

        # 将角度转化为弧度
        self.L1, self.B1, self.L2, self.B2 = m.radians(L1), m.radians(B1), m.radians(L2), m.radians(B2)

        # Ⅰ将椭球面元素投影到球面上
        # 由B求u
        self.u1 = m.atan(m.sqrt(1 - self.E.e1s) * m.tan(self.B1))
        self.u2 = m.atan(m.sqrt(1 - self.E.e1s) * m.tan(self.B2))
        # 由l求λ
        self.l = self.L2 - self.L1
        # 利用初值λ0=l计算λ1
        self.σ0 = m.acos(m.sin(self.u1) * m.sin(self.u2) + m.cos(self.u1) * m.cos(self.u2) * m.cos(self.l))

        self.m0 = m.asin(m.cos(self.u1) * m.cos(self.u2) * m.sin(self.l) / m.sin(self.σ0))
        self.k2 = self.E.e2s * m.cos(self.m0) * m.cos(self.m0)
        self.k4 = self.k2 * self.k2
        self.α2 = (1 / 2 + self.E.e1s / 8 - self.E.e1s * self.E.e1s / 16) * self.E.e1s - \
            self.E.e1s / 16 * (1 + self.E.e1s) * self.k2 + 3 / 128 * self.E.e1s * self.k4
        self.Δλ = self.α2 * self.σ0 * m.sin(self.m0)
        self.λ0 = self.l + self.Δλ
        self.Δσ = m.sin(self.m0) * self.Δλ
        self.σ1 = self.σ0 + self.Δσ
        self.m1 = m.asin(m.cos(self.u1) * m.cos(self.u2) * m.sin(self.λ0) / m.sin(self.σ1))
        self.A10 = m.atan(m.sin(self.λ0) / (m.cos(self.u1) * m.tan(self.u2) - m.sin(self.u1) * m.cos(self.λ0)))
        if self.A10 < 0:
            self.A10 += m.pi
        if self.m1 < 0:
            self.A10 += m.pi
        self.M1 = m.atan(m.sin(self.u1) * m.tan(self.A10) / m.sin(self.m1))
        if self.M1 < 0:
            self.M1 += m.pi

        self.k2 = self.E.e2s * m.cos(self.m1) * m.cos(self.m1)
        self.k4 = self.k2 * self.k2
        self.α2 = (1 / 2 + self.E.e1s / 8 - self.E.e1s * self.E.e1s / 16) * self.E.e1s - \
            self.E.e1s / 16 * (1 + self.E.e1s) * self.k2 + 3 / 128 * self.E.e1s * self.k4
        self.β2 = self.E.e1s / 16 * (1 + self.E.e1s) * self.k2 - self.E.e1s / 32 * self.k4
        self.λ = self.l + m.sin(self.m1) * (self.α2 * self.σ1 + self.β2 * m.sin(self.σ1) * m.cos(2 * self.M1 + self.σ1))

        # Ⅱ解算球面三角形
        # 求σ
        self.σ = m.acos(m.sin(self.u1) * m.sin(self.u2) + m.cos(self.u1) * m.cos(self.u2) * m.cos(self.λ))
        # 求self.A1、self.A2
        self.A1 = m.atan(m.sin(self.λ) / (m.cos(self.u1) * m.tan(self.u2) - m.sin(self.u1) * m.cos(self.λ)))
        self.m = m.asin(m.cos(self.u1) * m.sin(self.A1))
        if self.A1 < 0:
            self.A1 += m.pi
        if self.m > 0:
            self.A1 += m.pi
        self.M = m.atan(m.sin(self.u1) * m.tan(self.A10) / m.sin(self.m1))
        if self.M < 0:
            self.M += m.pi
        self.A2 = m.atan(m.sin(self.λ) / (m.sin(self.u2) * m.cos(self.λ) - m.tan(self.u1) * m.cos(self.u2)))
        if self.A2 < 0:
            self.A2 += m.pi
        if self.m < 0:
            self.A2 += m.pi

        # Ⅲ将椭球面元素换算到球面上
        self.k2 = self.E.e2s * m.cos(self.m) * m.cos(self.m)
        self.k4 = self.k2 * self.k2
        self.k6 = self.k4 * self.k2 * self.t1
        self.α1 = m.sqrt(1 + self.E.e2s) / self.E.a * (1 - self.k2 / 4 + 7 / 64 * self.k4 - 15 / 256 * self.k6)
        self.β1 = self.k2 / 4 - self.k4 / 8 + 37 / 512 * self.k6
        self.γ1 = (self.k4 - self.k6) / 128 * self.t2
        self.S = 1 / self.α1 * (self.σ - self.β1 * m.sin(self.σ) * m.cos(2 * self.M + self.σ) -
                                self.γ1 * m.sin(2 * self.σ) * m.cos(4 * self.M + 2 * self.σ))

        self.Result = [self.A1 * 180 / m.pi, self.A2 * 180 / m.pi, self.S]
        return self.Result


class Point():
    # 建立点类
    def LBAS(self, L1, B1, A1, S, T):  # 建立正算点类
        self.L1, self.B1, self.A1, self.S, self.T = L1, B1, A1, S, T
        self.P = Bessel()
        self.Result = self.P.Direct(self.L1, self.B1, self.A1, self.S, self.T)
        self.L2, self.B2, self.A2 = self.Result[0], self.Result[1], self.Result[2]

    def LBLB(self, L1, B1, L2, B2, T):  # 建立反算点类
        self.L1, self.B1, self.L2, self.B2, self.T = L1, B1, L2, B2, T
        self.P = Bessel()
        self.Result = self.P.Inverse(self.L1, self.B1, self.L2, self.B2, self.T)
        self.A1, self.A2, self.S = self.Result[0], self.Result[1], self.Result[2]

（2）DOS接口程序

import BesselQ
import os


SolveType = input('请输入解算类型：（键入D为正算，I为反算）\n')
while True:
    if SolveType == 'D' or SolveType == 'd':
        P1 = input('请依次输入P1点的坐标（L1，B1），方位角A1及大地线长S，中间用空格隔开：\n')
        while True:
            while True:
                try:
                    [L1, B1, A1, S] = [float(n) for n in P1.split()]
                    break
                except:
                    P1 = input('输入错误，请重新输入P1点的坐标（L1，B1），方位角A1及大地线长S，中间用空格隔开：\n')
            T = eval(input('请输入精度要求：（高于米级为1，米级为2，低于百米级为3）\n'))
            if T == 1 or 2 or 3:
                pass
            else:
                T = eval(input('输入错误，请重新输入精度要求：（高于米级为1，米级为2，低于百米级为3）\n'))
            P = BesselQ.Point()
            try:
                P.LBAS(L1, B1, A1, S, T)
                break
            except:
                P1 = input('输入错误，请重新输入P1点的坐标（L1，B1），方位角A1及大地线长S，中间用空格隔开：\n')
        L1, B1, A1, S, L2, B2, A2 = str(L1), str(B1), str(A1), str(S), str(P.L2), str(P.B2), str(P.A2)
        print('您输入P1点的坐标为：（' + L1 + '，' + B1 + '）\n方位角为：' + A1 + ',大地线长为：' + S)
        print('得到P2点的坐标为：（' + L2 + '，' + B2 + '）\n方位角为：' + A2)
        break

    elif SolveType == 'I' or SolveType == 'i':
        P1 = input('请依次输入P1点的坐标（L1，B1）及P2点的坐标（L2，B2），中间用空格隔开：\n')
        while True:
            while True:
                try:
                    [L1, B1, L2, B2] = [float(n) for n in P1.split()]
                    break
                except:
                    P1 = input('输入错误，请重新输入P1点的坐标（L1，B1）及P2点的坐标（L2，B2），中间用空格隔开：\n')
            T = eval(input('请输入精度要求：（高于米级为1，米级为2，低于百米级为3）\n'))
            if T == 1 or 2 or 3:
                pass
            else:
                T = eval(input('输入错误，请重新输入精度要求：（高于米级为1，米级为2，低于百米级为3）\n'))
            P = BesselQ.Point()
            try:
                P.LBLB(L1, B1, L2, B2, T)
                break
            except:
                P1 = input('输入错误，请重新输入P1点的坐标（L1，B1）及P2点的坐标（L2，B2），中间用空格隔开：\n')
        L1, B1, A1, S, L2, B2, A2 = str(L1), str(B1), str(P.A1), str(P.S), str(L2), str(B2), str(P.A2)
        print('您输入：\nP1点的坐标为：（' + L1 + '，' + B1 + '）\nP2点的坐标为：（' + L2 + '，' + B2 + '）')
        print('得到：\nP1点的方位角为：' + A1 + '\nP2点的方位角为：' + A2 + '\n大地线长为：' + S)
        break

    else:
        SolveType = input('输入错误，请重新输入解算类型：（键入D为正算，I为反算）\n')
os.system('pause')

---

五、MATLAB程序

（1）贝塞尔大地问题正算

% 大地问题正算
clear
clc
[Result] = Direct(90.1234, 34.5678, 100.1001, 15000000, 'High');
% 输入（L1,B1,A1,S,精度要求）
% 精度要求：高于米级为High，米级为Middle，低于百米级为Low

format long g
Result

%% 正算函数
function [Result] = Direct(L1, B1, A1, S, T)
% 贝塞尔大地问题正算函数，T为解算精度类型，高于米级为High，米级为Middle，低于百米级为Low
% 返回结果为[L2, B2, A2]

% 导入椭球数据，采用SGCS2000中国大地坐标系数据
a = 6378137.0;  % 长半轴
e1s = 0.0818191910428^2;  % 第一偏心率的平方
e2s = e1s / (1 - e1s);  % 第二偏心率的平方

% 将角度转化为弧度
L1 = deg2rad(L1);
B1 = deg2rad(B1);
A1 = deg2rad(A1);

% 实例化精度类型
Type = struct('High', [1, 1], 'Middle', [0, 1], 'Low', [0, 0]);
t1 = Type.(T)(1);
t2 = Type.(T)(2);

% Ⅰ将椭球面元素投影到球面上
% 由B1求u1
u1 = atan(sqrt(1 - e1s) * tan(B1));
% 计算辅助量M、m
M = atan(tan(u1) / cos(A1));
if M < 0
    M = M + pi;
end
m = asin(cos(u1) * sin(A1));
if m < 0
    m = m + 2 * pi;
end
% 将S化为Sigma
k2 = e2s * cos(m)^2;
k4 = k2^2;
k6 = k2^3 * t1;
Rho = 180 / pi * 3600;
Alpha1 = sqrt(1 + e2s) / a * (1 - k2 / 4 + 7 / 64 * k4 - 15 / 256 * k6);
Beta1 = k2 / 4 - k4 / 8 + 37 / 512 * k6;
Gamma1 = (k4 - k6) / 128 * t2;
Sigma1 = Alpha1 * S;
while true
    Sigma2 = Alpha1 * S + Beta1 * sin(Sigma1) * cos(2 * M + Sigma1) + Gamma1 * sin(2 * Sigma1) * cos(4 * M + 2 * Sigma1);
    if abs(Sigma2 - Sigma1) < 0.1 / Rho / 3600
        break
    else
        Sigma1 = Sigma2;
    end
end
Sigma = Sigma2;

% Ⅱ在球面上解算
% 求A2
A2 = atan(tan(m) / cos(M + Sigma));
if A2 < 0
    A2 = A2 + pi;
end
if A1 < pi
    A2 = A2 + pi;
end
% 求u2
u2 = atan(-cos(A2) * tan(M + Sigma));
% 求Lambda
Lambda1 = atan(sin(u1) * tan(A1));
if Lambda1 < 0
    Lambda1 = Lambda1 + pi;
end
if m > pi
    Lambda1 = Lambda1 + pi;
end
Lambda2 = atan(sin(u2) * tan(A2));
if Lambda2 < 0
    Lambda2 = Lambda2 + pi;
end
if m < pi
    if M + Sigma > pi
        Lambda2 = Lambda2 + pi;
    end
else
    if M + Sigma < pi
        Lambda2 = Lambda2 + pi;
    end
end
Lambda = Lambda2 - Lambda1;

% Ⅲ将球面元素换算到椭球面上
% 由u2求B2
B2 = atan(sqrt(1 + e2s) * tan(u2));
% 求L2
Alpha2 = (e1s / 2 + e1s^2 / 8 - e1s^3 / 16) - t1 * (e1s / 16 * (1 + e1s) * k2 - 3 / 128 * e1s * k4);
Beta2 = t2 * (e1s / 16 * (1 + t1 * e1s) * k2 - t1 * e1s / 32 * k4);
Gamma2 = t2 * e1s / 256 * k4;
L2 = L1 + Lambda - sin(m) * (Alpha2 * Sigma + Beta2 * sin(Sigma) * cos(2 * M + Sigma) + Gamma2 * sin(2 * Sigma) * cos(4 * M + 2 * Sigma));

Result = [L2, B2, A2] * 180 / pi;
end

（2）贝塞尔大地问题反算

% 大地问题反算
clear
clc
[Result] = Inverse(90.1234, 34.5678, 234.5678, -32.1098, 'High');
% 输入（L1,B1,L2,B2,精度要求）
% 精度要求：高于米级为High，米级为Middle，低于百米级为Low

format long g
Result

%% 反算函数
function [Result] = Inverse(L1, B1, L2, B2, T)
% 贝塞尔大地问题反算函数，T为解算精度类型，高于米级为High，米级为Middle，低于百米级为Low
% 返回结果为[A1, A2, S]

% 导入椭球数据，采用SGCS2000中国大地坐标系数据
a = 6378137.0;  % 长半轴
e1s = 0.0818191910428^2;  % 第一偏心率的平方
e2s = e1s / (1 - e1s);  % 第二偏心率的平方

% 将角度转化为弧度
L1 = deg2rad(L1);
B1 = deg2rad(B1);
L2 = deg2rad(L2);
B2 = deg2rad(B2);

% 实例化精度类型
Type = struct('High', [1, 1], 'Middle', [0, 1], 'Low', [0, 0]);
t1 = Type.(T)(1);
t2 = Type.(T)(2);

% Ⅰ将椭球面元素投影到球面上
% 由B求u
u1 = atan(sqrt(1 - e1s) * tan(B1));
u2 = atan(sqrt(1 - e1s) * tan(B2));
% 由l求Lambda
l = L2 - L1;
% 利用初值Lambda0=l计算Lambda1
Sigma0 = acos(sin(u1) * sin(u2) + cos(u1) * cos(u2) * cos(l));

m0 = asin(cos(u1) * cos(u2) * sin(l) / sin(Sigma0));
k2 = e2s * cos(m0)^2;
k4 = k2^2;
Alpha2 = (e1s / 2 + e1s^2 / 8 - e1s^3 / 16) - e1s / 16 * (1 + e1s) * k2 + 3 / 128 * e1s * k4;
DeltaLambda = Alpha2 * Sigma0 * sin(m0);
Lambda0 = l + DeltaLambda;
DeltaSigma = sin(m0) * DeltaLambda;
Sigma1 = Sigma0 + DeltaSigma;
m1 = asin(cos(u1) * cos(u2) * sin(Lambda0) / sin(Sigma1));
A10 = atan(sin(Lambda0) / (cos(u1) * tan(u2) - sin(u1) * cos(Lambda0)));
if A10 < 0
    A10 = A10 + pi;
end
if m1 < 0
    A10 = A10 + pi;
end
M1 = atan(sin(u1) * tan(A10) / sin(m1));
if M1 < 0
    M1 = M1 + pi;
end
k2 = e2s * cos(m1)^2;
k4 = k2^2;
Alpha2 = (e1s / 2 + e1s^2 / 8 - e1s^3 / 16) - e1s / 16 * (1 + e1s) * k2 + 3 / 128 * e1s * k4;
Beta2 = e1s / 16 * (1 + e1s) * k2 - e1s / 32 * k4;
Lambda = l + sin(m1) * (Alpha2 * Sigma1 + Beta2 * sin(Sigma1) * cos(2 * M1 + Sigma1));

% Ⅱ解算球面三角形
% 求Sigma
Sigma = acos(sin(u1) * sin(u2) + cos(u1) * cos(u2) * cos(Lambda));
% 求A1、A2
A1 = atan(sin(Lambda) / (cos(u1) * tan(u2) - sin(u1) * cos(Lambda)));
m = asin(cos(u1) * sin(A1));
if A1 < 0
    A1 = A1 + pi;
end
if m > 0
    A1 = A1 + pi;
end
M = atan(sin(u1) * tan(A10) / sin(m1));
if M < 0
    M = M + pi;
end
A2 = atan(sin(Lambda) / (sin(u2) * cos(Lambda) - tan(u1) * cos(u2)));
if A2 < 0
    A2 = A2 + pi;
end
if m < 0
    A2 = A2 + pi;
end

% Ⅲ将椭球面元素换算到球面上
k2 = e2s * cos(m)^2;
k4 = k2^2;
k6 = k2^3 * t1;
Alpha1 = sqrt(1 + e2s) / a * (1 - k2 / 4 + 7 / 64 * k4 - 15 / 256 * k6);
Beta1 = k2 / 4 - k4 / 8 + 37 / 512 * k6;
Gamma1 = (k4 - k6) / 128 * t2;
S = 1 / Alpha1 * (Sigma - Beta1 * sin(Sigma) * cos(2 * M + Sigma) - Gamma1 * sin(2 * Sigma) * cos(4 * M + 2 * Sigma));

Result = [A1, A2, S];
Result(1:2) = Result(1:2) * 180 / pi;

end

---

六、运行结果

1、Python运行结果

（1）贝塞尔大地问题正算

（2）贝塞尔大地问题反算

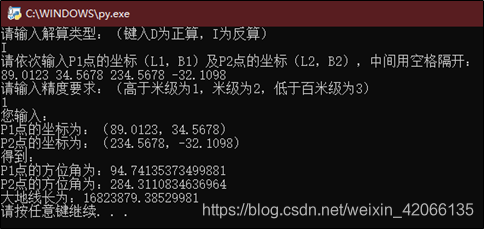
2、MATLAB运行结果

（1）贝塞尔大地问题正算

（2）贝塞尔大地问题反算

---

七、文件下载地址

Python程序文件下载地址：【椭球大地测量学】Python实现贝塞尔大地问题正反解计算编程（含流程图）
MATLAB程序文件下载地址：【椭球大地测量学】MATLAB实现贝塞尔大地问题正反解计算编程（含流程图）

---

欢迎交流！