将三角形绕点b顺时针旋转90度_中考难点，聚焦费马点问题及拓展探究，体验旋转构造的魅力...

有一类涉及三条线段和最短问题，求解方法独特，主要是利用旋转的性质转化为两点之间线段最短的问题，比较重要的就是费马点问题，这类问题常常出现中考压轴题中最值问题和自主招生试卷中的问题中，相当一部分学生由于构造转化思想运用不合理，导致解不出问题，中考复习时有必要了解一点。

费马点前生

皮耶·德·费马(Pieme de Fermat)是一个17世纪的法国律师，也是一位业余数学家。之所以称业余，是由于皮耶德·费马具有律师的全职工作，他的姓氏根据法文与英文实际发普也常译为"费尔玛"(注意"玛"字)。

费马最后定理在中国习惯称为费马大定理，西方数学界原名"最后"的意思是：其它猜想都证实了，这是最后一个，著名的数学史学家灵尔(E，T.Bell)在20世纪初所援写的著作中，称皮那·德·费马为"业余数学家之王"，贝尔深信，费马比皮那德费马同时代的大多数专业数学家更有成就，然而皮那德·费马并未在其他方面另有成就，本人也渐渐退出人们的视野，考虑到17世纪是杰出数学家活跃的世纪，因而贝尔认为费马是17世纪数学家中最多产的明星。

费马点问题最平是由法国数学家皮疾尔德费马在一封写给意大利数学家疾万杰利新塔托里拆利(气压计的发明者)的信中提出的，托里折利最半解决了这个问题，而19世纪的数学家新坦纳重新发现了这个问题，并系统地进行了推广，因此这个点也称为托里折利点或斯坦纳点，相关的问题也被称作费马-托里折利-斯过纳问题，这一问题的解决极大推动了联合数学的发展，在近代数学史上具有里程碑式的意义。

费马点性质探究

引例：如图在Rt△ABC，∠C=45°，AC=2√２。内找一点P，使得PA+PB+PC最小.

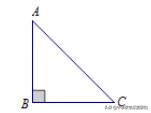
【解析】如图，在三角形内部任取一点P，连接AP、PC、PB。

将△APC绕点A旋转得△AP´C´，从而有PA+PB+PC=P´A+P´C+BP故要使得PA+PB+PC最小，

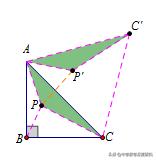
我们可以考虑

1 AP´转化为PＰ´；②BPP´C四点共线．故而有∠PAP'=60°(易得旋转60°),

∠APC=∠APB=∠BPC=120°，可得(PA+PB+PC)min=BC´,从而根据上数据，易得(PA+PB+PC)min=BC´=√2+√6.

【方法归纳】如图，到三角形三个顶点距离和最小的点，我们称其为费马点。从上探究中，我们可以得出，对于费马点而言：

1、费马点问题的解决方法为旋转变换。

2、费马点满足其所对三边张角相等(∠APC=∠APB=∠BPC=120°)，故也称为三角形等角中心。

3、费马点确定：

①辅助圆做等角(120°)B's②三角形任意两边向外做等边三角形

(如图：△ACD和ABB´)，则等边三角形顶点与三角形对顶点连线交点记为费马点(如图：B'C和BD交点P)

4、费马点问题求线段长

以三角形任一边向外做等边三角形，所做等边三角形(外)顶点及所对三角形顶点连线，即为所求。(如图B´C或BD均可)

费马点应用问题探究

1．(2019•锡山区校级二模)如图，已知矩形ABCD，AB＝4，BC＝6，点M为矩形内一点，点E为BC边上任意一点，则MA+MD+ME的最小值为(　　)

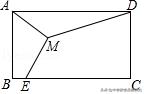
A．3+2√2 B．4+3√3 C．2+2√13 D．10

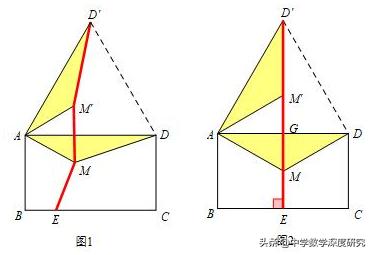
【解析】：将△AMD绕点A逆时针旋转60°得到△AM'D'，MD＝M'D'，易得到△ADD'和△AMM'均为等边三角形，∴AM＝MM'，∴MA+MD+ME＝D'M+MM'+ME，

∴D′M、MM′、ME共线时最短，

由于点E也为动点，

∴当D'E⊥BC时最短，此时易求得D'E＝DG+GE＝4+3√3，

∴MA+MD+ME的最小值为4+3√3．故选：B．

本题考查轴对称、旋转变换、矩形的性质等知识，解题的关键是学会添加常用辅助线，构造等边三角形解决问题，学会用转化的思想思考问题，属于中考选择题中的压轴题．

变式1．(2018春•滨湖区期末)如图，在▱ABCD中，AB＝4，BC＝6，∠ABC＝60°，点P为▱ABCD内一点，点Q在BC边上，则PA+PD+PQ的最小值为(　　)

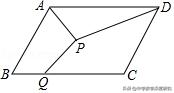
A．√3+√7+√19 B．6+2√3 C．5√3 D．10

【解析】：∵▱ABCD中，∠ABC＝60°，∴AD&#