【CodeForces 1066F】离散化 | 贪心 | 简化极角排序 | 动态规划 | N

最新推荐文章于 2021-03-14 22:20:13 发布

Keyu Tian

最新推荐文章于 2021-03-14 22:20:13 发布

阅读量825

点赞数 2

分类专栏： T | 贪心 D | DP(其他) C | CodeForces L | 离散化文章标签： CodeForces 贪心 DP

本文链接：https://blog.csdn.net/weixin_42102584/article/details/83225820

版权

C | CodeForces 同时被 3 个专栏收录

15 篇文章 0 订阅

订阅专栏

T | 贪心

9 篇文章 0 订阅

订阅专栏

D | DP(其他)

7 篇文章 0 订阅

订阅专栏

1066F. Yet another 2D Walking

time limit per test: 4 seconds

memory limit per test: 256 megabytes

URL

http://codeforces.com/contest/1066/problem/F

Tags

离散化 + 贪心 + 简化极角排序 + DP

Introduction

平面坐标系xOy，给出n个整点，每个点 (x, y) 的层数定义为 max{x, y}。

一个人从原点出发，并且按层数非递减顺序访问每个点。

求最短路径长度和（距离是曼哈顿距离，即竖直/水平折线的距离）。

Input

Codeforces老规矩，一组输入。第一行是点的个数（数据范围2e5，能猜到应该是nlogn的解法），接下来V行是每个点的 x y 坐标

Output

输出最短距离和

Sample Input

8
2 2
1 4
2 3
3 1
3 4
1 1
4 3
1 2

Sample Output

15

图解：

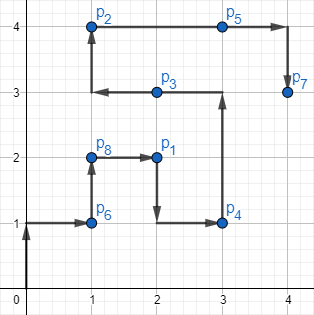
Analysis & AC Code

分析如下：

① 离散化
- 把层号离散化，因为坐标可能非常大，但是层数最多不超过点的个数。为了存下每层信息，需要离散化。这里要用到一次排序，时间复杂度 O(nlogn)
② 贪心
- 按层走，在每一层内部走的时候，最短路的走法一定是按顺时针走过本层内所有点（不回头）或者按逆时针走。并且由于是曼哈顿距离，如不这样走的话，最终解一定不会为最优解（一定会绕远）所以贪心算法适用。时间复杂度 Θ(n)
③ 简化版极角排序
- 对所有点排序，时间复杂度 O(nlogn) （当然这里的排序可以和用来离散化的排序在一起进行）（不在同一层的点，层数小的排在前面；在同一层的，x小的或者 x相等但y大的排在前面，这样就可以把同一层内的点按照顺时针排好）然后就可以：
1. 对每一层进行完整的顺序遍历，进而求出每一层内部的路径和
2. 为之后dp状态转移做好基础（把每一层最左上的点排在了vector的最前、最右下的点排在了vector的最后，便于dp状态转移时求层间距）
④ DP
- 首先这里满足无后效性（对于之前层不同的走法，只要累计路径和相同，就可以认为这些不同的走法都是相同的，即选择任何一个都不会影响后续的最优解）和最优子结构性质（最终最优解的中途解也是对应的最优解，否则最终解还可以更小，那就不是最优解了），所以dp算法适用。
- 然后再分析具体如何dp。每一层都可能以顺时针方向通过，或者以逆时针方向通过，所以跟本层走法有关；并且跟上一层是顺时针还是逆时针也有关（决定着状态转移时层间距是多少）。很自然地就可以想到二维DP，第一维就是层编号，第二维表示这一层是顺时针通过的还是逆时针通过的。dp结束后取 min{ dp[level_count-1][R], dp[level_count-1][S] } 就是最终答案。时间复杂度 Θ(n)
- dp 详细思路
  - 【定义】：dp[i][R] 表示走到第i层最后一个点，并且第i层是顺时针通过的；dp[i][S] 表示走到第i层最后一个点，并且第i层是逆时针通过的
  - 【初始化】：dp[0][R] = dp[0][S] = dist_sum[0]（dist_sum[0]就是第0层内部的路径和，在本题第0层只有一个点(原点)，所以其实就是0）
  - 【递推顺序】：循环第一维 [1, level_count）（从第一层到最后一层dp最优路径和）
  - 【状态转移方程】：dist(↖↘) 表示上一层最左上的点和这一层最右下的点之间的曼哈顿距离，以此类推。
    - dp[i][R] = min
      - {
      - dp[i-1][R] + dist(↘↖) + dist_sum[i] (上层顺这层顺，层间路径是上层终点↘和这层起点↖的连接)
      - dp[i-1][S] + dist(↖↖) + dist_sum[i] (上层逆这层顺，层间路径是上层终点↖和这层起点↖的连接)
      - }
    - dp[i][S] = min
      - {
      - dp[i-1][R] + dist(↘↘) + dist_sum[i] (上层顺这层逆，层间路径是上层终点↘和这层起点↘的连接)
      - dp[i-1][S] + dist(↖↘) + dist_sum[i] (上层逆这层逆，层间路径是上层终点↖和这层起点↘的连接)
      - }
  - 【答案】：min{ dp[level_count-1][R], dp[level_count-1][S] }

总时间复杂度 O(nlogn)，空间复杂度 Θ(n)

代码：

#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>

#define LL long long
#define sc(x) {register char _c=getchar(),_v=1;for(x=0;_c<48||_c>57;_c=getchar())if(_c==45)_v=-1;for(;_c>=48&&_c<=57;x=(x<<1)+(x<<3)+_c-48,_c=getchar());x*=_v;}
#define PC putchar
#define MAX(a, b) (a>b?a:b)
#define MIN(a, b) (a<b?a:b)
#define DIST(p1, p2) ((p1.x>p2.x?p1.x-p2.x:p2.x-p1.x)+(p1.y>p2.y?p1.y-p2.y:p2.y-p1.y))
void PRT(const LL a){if(a<0){PC(45),PRT(-a);return;}if(a>=10)PRT(a/10);PC(a%10+48);}

constexpr int MN(200007);

enum RS_DIR
{
	R, S, RS_CNT
};

struct Point
{
	int x, y;
	int level;

	inline bool operator <(const Point &o) const
	{
		return level < o.level || level == o.level && (y > o.y || y == o.y && x < o.x);
	}
} points[MN];

LL dist_sum[MN];
LL dp[MN][RS_CNT];
std::vector<Point> level[MN];

int main()
{
	int n;
	sc(n)
	++n;

	points[0].x = points[0].y = points[0].level = 0;
	for (auto it=points+1, E=points+n; it!=E; ++it)
	{
		sc((it->x))
		sc((it->y))
		it->level = MAX(it->x, it->y);
	}
	std::sort(points, points+n);

	int level_index = 0;
	for (int i=0; i<n-1; ++i)
	{
		level[level_index].push_back(points[i]);

		if (points[i].level == points[i+1].level)
			dist_sum[level_index] += DIST(points[i], points[i+1]);
		else
			++level_index;
	}
	level[level_index].push_back(points[n-1]);
	int level_cnt = level_index + 1;

	dp[0][R] = dp[0][S] = 0;
	for (int i=1; i<level_cnt; ++i)
	{
		LL R_R = dp[i-1][R] + DIST(level[i-1].back(), level[i].front()) + dist_sum[i];
		LL S_R = dp[i-1][S] + DIST(level[i-1].front(), level[i].front()) + dist_sum[i];
		if (R_R < S_R)
			dp[i][R] = R_R;
		else
			dp[i][R] = S_R;

		LL R_S = dp[i-1][R] + DIST(level[i-1].back(), level[i].back()) + dist_sum[i];
		LL S_S = dp[i-1][S] + DIST(level[i-1].front(), level[i].back()) + dist_sum[i];
		if (R_S < S_S)
			dp[i][S] = R_S;
		else
			dp[i][S] = S_S;
	}

	PRT(MIN(dp[level_cnt-1][R], dp[level_cnt-1][S]));

	return 0;
}

（刚刚打比赛的时候这道题是1:59:54 AC 的qwq）