图的Floyd算法——C/C++

最新推荐文章于 2025-03-13 09:52:08 发布
最新推荐文章于 2025-03-13 09:52:08 发布
阅读量5.7k 收藏 35
点赞数 13
分类专栏： 数据结构 文章标签： Floyd
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_42109012/article/details/94217203
版权
本文深入讲解了Floyd算法，一种用于解决多源最短路径问题的经典算法。文章详细阐述了算法原理，包括如何通过邻接矩阵求解图中任意两点间最短路径，并介绍了算法的实现步骤和代码示例。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

例子：
在这里插入图片描述

一、算法原理

  1. 通过一个图的权值矩阵求出它的每两点间的最短路径矩阵。
  2. 从图的带权邻接矩阵A=[a(i,j)]，n×n开始，递归地进行n次更新，即由矩阵D(0)=A，按一个公式，构造出矩阵D(1)；又用同样地公式由D(1)构造出D(2)；……；最后又用同样的公式由D(n-1)构造出矩阵D(n)。矩阵D(n)的i行j列元素便是i号顶点到j号顶点的最短路径长度，称D(n)为图的距离矩阵，同时还可引入一个后继节点矩阵path来记录两点间的最短路径。
  3. 采用松弛技术（松弛操作），对在i和j之间的所有其他点进行一次松弛。所以时间复杂度为O(n^3);

二、算法思想

1. 从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。
2. 对于每一对顶点 u 和v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比已知的路径更短。如果是更新它。
3. 把图用邻接矩阵G表示出来，如果从Vi到Vj有路可达，则G[i][j]=d，d表示该路的长度；否则G[i][j]=无穷大。定义一个矩阵D用来记录所插入点的信息，D[i][j]表示从Vi到Vj需要经过的点，初始化D[i][j]=j。把各个顶点插入图中，比较插点后的距离与原来的距离，G[i][j]= min( G[i][j], G[i][k]+G[k][j] )，如果G[i][j]的值变小，则D[i][j]=k。在G中包含有两点之间最短道路的信息，而在D中则包含了最短通路径的信息。
4. 比如，要寻找从V5到V1的路径。根据D，假如D(5,1)=3则说明从V5到V1经过V3，路径为{V5,V3,V1}，如果D(5,3)=3，说明V5与V3直接相连，如果D(3,1)=1，说明V3与V1直接相连。

三、算法实现

1、Floyd算法

void Floyd(MatGraph MG) {
	int i, j, k;
	int A[MAXV][MAXV];
	int path[MAXV][MAXV];
	for (i = 0; i < MG.n; i++) {
		for (j = 0; j < MG.n; j++) {
			A[i][j] = MG.adjMat[i][j];
			if (i != j && MG.adjMat[i][j] < INF) {
				path[i][j] = i;							//顶点 i 到顶点 j 有边时
			}
			else {
				path[i][j] = -1;						//顶点 i 到顶点 j 无边时
			}
		}
	}
	for (k = 0; k < MG.n; k++) {						//一次考察所有顶点
		for (i = 0; i < MG.n; i++) {
			for (j = 0; j < MG.n; j++) {
				if (A[i][j] > A[i][k] + A[k][j]) {
					A[i][j] = A[i][k] + A[k][j];		//修改最短路径长度
					path[i][j] = path[k][j];			//修改最短路径
				}
			}
		}
	}
	displayPath(MG, A, path);							//输出最短路径
}

2、输出多源最短路径

void displayPath(MatGraph MG, int A[MAXV][MAXV], int path[MAXV][MAXV]) {
	int i, j, k;
	int s;
	int aPath[MAXV];										//存放一条最短路径（逆向）
	int d;													//顶点个数
	for (i = 0; i < MG.n; i++) {
		for (j = 0; j < MG.n; j++) {
			if (A[i][j] != INF && i != j) {					//若顶点 i 和 顶点 j 之间存在路径
				printf("从 %d 到 %d 的路径为：", i, j);
				k = path[i][j];
				d = 0;
				aPath[d] = j;								//路径上添加终点
				while (k != -1 && k != i) {					//路劲上添加中间点
					d++;
					aPath[d] = k;
					k = path[i][k];
				}
				d++;
				aPath[d] = i;								//路径上添加起点
				printf("%d", aPath[d]);						//输出起点
				for (s = d - 1; s >= 0; s--) {				//输出路径上其他顶点
					printf("->%d", aPath[s]);
				}
				printf("\t\t");
				printf("路径长度为：%d\n", A[i][j]);
			}
		}
	}
}

四、整体框架

#include<stdio.h>
#include<malloc.h>

#define MAXV 7					//最大顶点个数 
#define INF 32767				//定义 ∞
//∞ == 32767 ,int 型的最大范围（2位）= 2^(2*8-1)，TC告诉我们int占用2个字节，而VC和LGCC告诉我们int占用4个字节
//图：Graph
//顶点：Vertex
//邻接：Adjacency
//矩阵：Matrix
//表：List
//边：Edge 

typedef struct vertex {
	int number;					//顶点的编号 	
}VertexType; 					//别名，顶点的类型 

typedef struct matrix {
	int n;						//顶点个数
	int e;						//边数 
	int adjMat[MAXV][MAXV];		//邻接矩阵数组			
	VertexType ver[MAXV];		//存放顶点信息 
}MatGraph;						//别名，完整的图邻接矩阵类型

typedef struct eNode {
	int adjVer;					//该边的邻接点编号 
	int weiLGht;				//该边的的信息，如权值 
	struct eNode* nextEdLGe;	//指向下一条边的指针 
}EdgeNode; 						//别名，边结点的类型 

typedef struct vNode {
	EdgeNode* firstEdLGe;		//指向第一个边结点 
}VNode; 						//别名，邻接表的头结点类型 

typedef struct list {
	int n;						//顶点个数
	int e;						//边数
	VNode adjList[MAXV];		//邻接表的头结点数组 
}ListGraph;						//别名，完整的图邻接表类型 

//创建图的邻接表 
void createAdjListGraph(ListGraph*& LG, int A[MAXV][MAXV], int n, int e) {
	int i, j;
	EdgeNode* p;
	LG = (ListGraph*)malloc(sizeof(ListGraph));
	for (i = 0; i < n; i++) {
		LG->adjList[i].firstEdLGe = NULL;						//给邻接表中所有头结点指针域置初值 
	}
	for (i = 0; i < n; i++) {									//检查邻接矩阵中的每个元素 
		for (j = n - 1; j >= 0; j--) {
			if (A[i][j] != 0) {									//存在一条边 
				p = (EdgeNode*)malloc(sizeof(EdgeNode));		//申请一个结点内存
				p->adjVer = j;									//存放邻接点 
				p->weiLGht = A[i][j];							//存放权值
				p->nextEdLGe = NULL;

				p->nextEdLGe = LG->adjList[i].firstEdLGe;		//头插法 
				LG->adjList[i].firstEdLGe = p;
			}
		}
	}
	LG->n = n;
	LG->e = e;
}

//输出邻接表 
void displayAdjList(ListGraph* LG) {
	int i;
	EdgeNode* p;
	for (i = 0; i < MAXV; i++) {
		p = LG->adjList[i].firstEdLGe;
		printf("%d:", i);
		while (p != NULL) {
			if (p->weiLGht != 32767) {
				printf("%2d[%d]->", p->adjVer, p->weiLGht);
			}
			p = p->nextEdLGe;
		}
		printf(" NULL\n");
	}
}

//输出邻接矩阵
void displayAdjMat(MatGraph MG) {
	int i, j;
	for (i = 0; i < MAXV; i++) {
		for (j = 0; j < MAXV; j++) {
			if (MG.adjMat[i][j] == 0) {
				printf("%4s", "0");
			}
			else if (MG.adjMat[i][j] == 32767) {
				printf("%4s", "∞");
			}
			else {
				printf("%4d", MG.adjMat[i][j]);
			}
		}
		printf("\n");
	}
}

//邻接表转换为邻接矩阵
void ListToMat(ListGraph* LG, MatGraph& MG) {
	int i, j;
	EdgeNode* p;
	for (i = 0; i < MAXV; i++) {
		for (j = 0; j < MAXV; j++) {
			MG.adjMat[i][j] = 0;
		}
	}
	for (i = 0; i < LG->n; i++) {
		p = LG->adjList[i].firstEdLGe;
		while (p != NULL) {
			MG.adjMat[i][p->adjVer] = p->weiLGht;
			p = p->nextEdLGe;
		}
	}
	MG.n = LG->n;
	MG.e = LG->e;
}

//输出多源最短路径
void displayPath(MatGraph MG, int A[MAXV][MAXV], int path[MAXV][MAXV]) {
	int i, j, k;
	int s;
	int aPath[MAXV];										//存放一条最短路径（逆向）
	int d;													//顶点个数
	for (i = 0; i < MG.n; i++) {
		for (j = 0; j < MG.n; j++) {
			if (A[i][j] != INF && i != j) {					//若顶点 i 和 顶点 j 之间存在路径
				printf("从 %d 到 %d 的路径为：", i, j);
				k = path[i][j];
				d = 0;
				aPath[d] = j;								//路径上添加终点
				while (k != -1 && k != i) {					//路劲上添加中间点
					d++;
					aPath[d] = k;
					k = path[i][k];
				}
				d++;
				aPath[d] = i;								//路径上添加起点
				printf("%d", aPath[d]);						//输出起点
				for (s = d - 1; s >= 0; s--) {				//输出路径上其他顶点
					printf("->%d", aPath[s]);
				}
				printf("\t\t");
				printf("路径长度为：%d\n", A[i][j]);
			}
		}
	}
}

//Floyd算法
void Floyd(MatGraph MG) {
	int i, j, k;
	int A[MAXV][MAXV];
	int path[MAXV][MAXV];
	for (i = 0; i < MG.n; i++) {
		for (j = 0; j < MG.n; j++) {
			A[i][j] = MG.adjMat[i][j];
			if (i != j && MG.adjMat[i][j] < INF) {
				path[i][j] = i;							//顶点 i 到顶点 j 有边时
			}
			else {
				path[i][j] = -1;						//顶点 i 到顶点 j 无边时
			}
		}
	}
	for (k = 0; k < MG.n; k++) {						//一次考察所有顶点
		for (i = 0; i < MG.n; i++) {
			for (j = 0; j < MG.n; j++) {
				if (A[i][j] > A[i][k] + A[k][j]) {
					A[i][j] = A[i][k] + A[k][j];		//修改最短路径长度
					path[i][j] = path[k][j];			//修改最短路径
				}
			}
		}
	}
	displayPath(MG, A, path);							//输出最短路径
}

int main() {
	ListGraph* LG;
	MatGraph MG;

	int array[MAXV][MAXV] = {
		{  0,  4,  6,  6,INF,INF,INF},
		{INF,  0,  1,INF,  7,INF,INF},
		{INF,INF,  0,INF,  6,  4,INF},
		{INF,INF,  2,  0,INF,  5,INF},
		{INF,INF,INF,INF,  0,INF,  6},
		{INF,INF,INF,INF,  1,  0,  8},
		{INF,INF,INF,INF,INF,INF,  0}
	};

	int e = 12;
	createAdjListGraph(LG, array, MAXV, e);
	displayAdjList(LG);
	printf("\n");

	ListToMat(LG, MG);
	displayAdjMat(MG);
	printf("\n");

	Floyd(MG);
	printf("\n");

	return 0;
}

五、结果展示

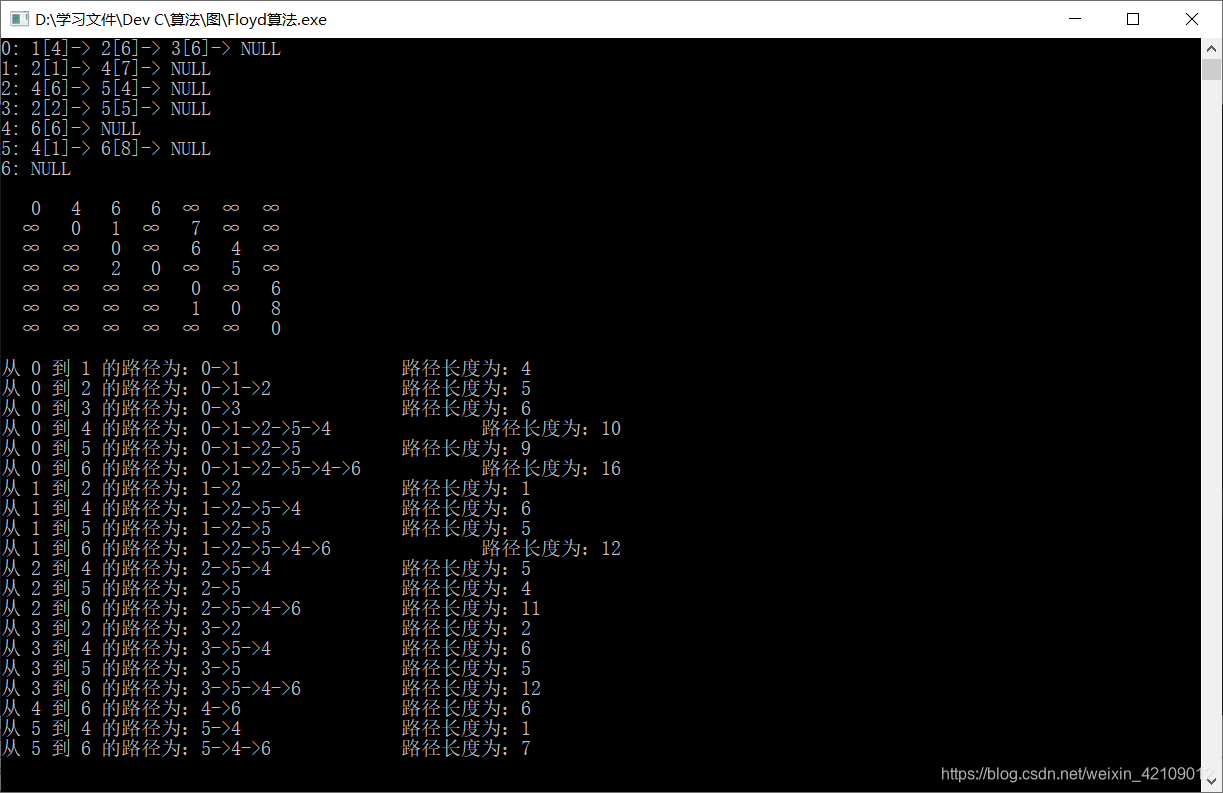
在这里插入图片描述

C++实现Floyd算法
Katalang的博客
05-18 1915
C++实现Floyd算法 Floyd算法是计算任意两点之间最短路的一种算法。相比于Dijkstra和逐次逼近法来说最大的优点在于可以全局的计算任意两点间的最短路径。相关原理很多博主写的都非常好，这里就不再赘述。 此代码是在完成作业是不想手动计算，有些题目迭代次数有点多，矩阵又比较庞大，容易算错失去耐心，故随手写了代码帮我计算。贴在此处也好供日后复习。因此代码没有经过很好的优化，不足之处欢迎批评指正。 代码如下 #include<iostream> #include <bits/stdc++
弗洛伊德（Floyd）算法c++版
weixin_46499682的博客
09-10 6913
弗洛伊德算法其实是一种非常简单的图论算法，总的来说，弗洛伊德算法甚至可以说是一种暴力枚举。 弗洛伊德算法是解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权（但不可存在负权回路）的最短路径问题，同时也被用于计算有向图的传递闭包。——弗洛伊德算法的定义。 从出发地到目的地的过程中，我们并不是一下子就到达目的地，而是要经过很多的中转站来帮助我们一步一步地到达目的地。例如下面的图中，假设 AB，BC 之间的距离分别为 7 和 2。我们看到，A 和 C 之间不能直接通达，因此，要计算 A ...
【C++算法详解】Floyd最短路径算法——动态规划的精妙实践（附完整代码）
最新发布
m0_69718028的博客
03-13 502
【C++算法详解】Floyd最短路径算法——动态规划的精妙实践（附完整代码）
C++实现floyd算法
09-06
C++实现floyd算法 希望大家指正出现的问题，多多下载，本人需要积分，谢谢大家
【C++】Floyd算法
weixin_63411324的博客
05-17 601
它以罗伯特·弗洛伊德（Robert Floyd）的名字命名，他在1962年独立发现了该算法，并以斯蒂芬·沃沙尔（Stephen Warshall）的名字描述了用于找到图的传递闭包的版本。：对于每一对顶点 (i, j)，以及可能的中间顶点k，检查是否可以通过k点使得从i到j的距离更短。具体来说，就是对于每个顶点k，遍历所有的顶点对(i, j)，并检查是否存在一条路径从i到k再到j的距离小于直接从i到j的距离。该算法通过迭代更新一个n×n的矩阵，其中包含图中所有顶点对之间的最短路径距离，其中n是顶点的数量。
Qt和C/C++实现的可视化景点旅游信息系统——包含详细注释与txt说明文件
11-24
5. 该项目包含 求两个景点间的最短路径的算法——Floyd 6. 该项目包含 给出道路建设(最小生成树)的算法——Kruskal 7. 该项目包含 自定义地图文件读入与写出的算法 阅读建议： 在下载压缩包后，务必细看 .txt 说明...
Floyd算法——C++
喜欢黄花鱼的猫
07-09 864
Floyd算法用于求每对顶点间的最短路径问题。问题描述：给定带权有向图G=（V,E），对任意顶点vi和vj（i！=j），求顶点vi到vj的最短路径。核心算法代码：void Floyd(MGraph G) { int i,j,k; int dist[MaxSize][MaxSize]={0}; for(i=0;i&lt;G.vertexNum;i++) ...
图论的一些算法——c语言、c++
05-31
Floyd算法是一种用于求解带权图中所有顶点之间最短路径的经典算法，其时间复杂度为\(O(V^3)\)，其中\(V\)表示顶点的数量。该算法能够处理负权边（但不能处理包含负权回路的情况），并且可以同时得到每个顶点对之间...
c++图论算法1——Floyd（弗洛伊德）算法
Ocean103的博客
12-04 3750
简单介绍弗洛伊德算法的工作原理，代码实现等
floyd算法的C++代码
07-25
floyd算法的C++代码，用的时候只要改几个参数就可以了
Floyd算法C++
04-12
用Floyd算法求每对结点最短路径。基于C++的类与模板。
算法——弗洛伊德算法（Floyd-Warshall）（图论）（c++）
Passerby_XX的博客
03-09 2785
（蒟蒻的第四篇文章，希望dalao勿喷） （希望没问题） 声明： 1.本人变量定义的名称很low 2.本人用的方法也很low 3.但我觉得文章应该不low（盲目自信） 第四篇文章讲讲Floyd算法 Floyd算法是一种寻找最短路径的常见算法，其特点是：短，好理解（虽然其他算法也挺好理解的 思路 Floyd算法的主要思路是在于： 比如你要坐飞机从A城到B城，结果你发现A到B的直达航班要999元！于是你漫无目的地继续看其他航班信息，结果突然发现在A和B中间，还有一个C城！而且A到C和B到C.
【Floyd算法的c++实现】
武帝为此的博客
03-17 569
该算法基于动态规划思想，其核心思想是利用中间节点的集合不断更新任意两点间的最短距离。具体实现中，Floyd算法通过枚举每一个中间节点，然后在该中间节点集合上对所有的节点对进行更新，最终得到任意两点间的最短路径。Floyd算法是一种经典的用于求解任意两点间最短路径的算法，由Robert W. Floyd于1962年提出，也称为Floyd-Warshall算法。Floyd算法的时间复杂度为O(n^3)，其中n为节点数，因此该算法适用于较小的图或者密集图，对于稀疏图或者规模较大的图，其运行时间会较长。
弗洛伊德(Floyd)算法（C/C++)
闻道有先后，术业有专攻
08-28 4433
弗洛伊德算法（Floyd's algorithm），又称为弗洛伊德-沃尔什算法（Floyd-Warshall algorithm），是一种用于在加权图中找到所有顶点对之间最短路径的算法。这个算法适用于有向图和无向图，并且可以处理负权重边，但不能处理负权重循环。
C++数据结构与算法分析——Floyd算法
l_red_forest的博客
10-15 3276
介绍 Floyd算法是一种求多源汇最短路的算法，它可以求出任意两点间的最短距离(如果这两点连通的话)，并且Floyd算法非常容易实现： 算法模板O(n3)O(n^3)O(n3) for(int k = 1; k <= n; k ++) for(int i = 1; i <= n; i ++) for(int j = 1; j <= n; j ++) d[i][j] = min(d[i][j],d[i][k] + d[k][j]); 它总共有3层循环，每层n次，所以时间复杂度为
最短路径---Floyd算法（C++）
Nick
12-05 6197
Floyd算法的介绍 算法的特点：  弗洛伊德算法是解决任意两点间的最短路径的一种算法，可以正确处理有向图或有向图或负权（但不可存在负权回路)的最短路径问题，同时也被用于计算有向图的传递闭包。 算法的思路 通过Floyd计算图G=(V,E)中各个顶点的最短路径时，需要引入两个矩阵，矩阵S中的元素a[i][j]表示顶点i(第i个顶点)到顶点j(第j个顶点)的距离。矩阵P中的元素b[i][j]，表...
Floyd算法简单实现（C++）
weixin_30497527的博客
01-14 466
图的最短路径问题主要包括三种算法： （1）Dijkstra (没有负权边的单源最短路径） （2）Floyed (多源最短路径) （3）Bellman (含有负权边的单源最短路径） 本文主要讲使用C++实现简单的Floyd算法，Floyd算法原理参见Floyd–Warshall algorithm Floyd算法简单实现（C++） 1 #include<iostream&...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值