题目
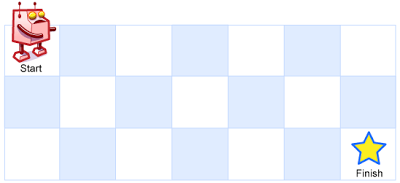
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
思路
由于网格中有障碍物,所以考虑的情况会比没有阻碍的情况要多。同样设置一个二维数组d[m][n]存储到达每个网格的路径数。
如果是第一行第一列的空格有障碍物,则d[0][0] = 0,否则d[0][0] = 1;
如果是第一列(行)中某个空格有障碍物(不包括第一行第一列的空格),那么有d[i][0] = 0 或者 d[0][i] = 0,否则有 d[i][0] = d[i-1][0] 或d[0][i] = d[0][i-1];
如果不在第一行也不在第一列,如果某个空格有障碍物,则到达这个空格的路径数为0,如果某个空格没有障碍物,则有d[i][j] = d[i-1][j] + d[i][j-1]。
代码1
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
if(obstacleGrid.empty() || obstacleGrid[0].empty()) return 0;
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
vector<vector<long>> d(m,vector<long>(n));
int i, j;
//判断起点
if(obstacleGrid[0][0] == 1) d[0][0] = 0;
else d[0][0] = 1;
//判断第一列
for(i = 1; i < m; i++)
{
if(obstacleGrid[i][0] == 1) d[i][0] = 0;
else d[i][0] = d[i-1][0];
}
//判断第一行
for(j = 1; j < n; j++)
{
if(obstacleGrid[0][j] == 1) d[0][j] = 0;
else d[0][j] = d[0][j-1];
}
//判断不是第一行也不是第一列的空格
for(i = 1; i < m; ++i)
{
for(j = 1; j < n; ++j)
{
if(obstacleGrid[i][j] == 1) d[i][j] = 0;
else
{
d[i][j] = d[i-1][j] + d[i][j-1];
}
}
}
return d[m-1][n-1];
}
代码2:改进使代码量减少,空间复杂度仍为o(n^2)
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
if(obstacleGrid.empty() || obstacleGrid[0].empty()) return 0;
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
vector<vector<long>> d(m,vector<long>(n));
int i, j;
for(i = 0; i < m; i++)
{
for(j = 0; j < n; j++)
{
//如果当前空格有障碍物,则到达该空格的路径数必为0
if(obstacleGrid[i][j] == 1) d[i][j] = 0;
//如果当前空格没有障碍物
else
{
//当前空格处于起始点
if(i == 0 && j == 0) d[i][j] = 1;
//当前空格处于第一行且不是起始位置
else if(i == 0) d[i][j] = d[i][j-1];
//当前空格处于第一列且不是起始位置
else if(j == 0) d[i][j] = d[i-1][j];
//当前空格既不在第一行也不在第一列
else d[i][j] = d[i-1][j] + d[i][j-1];
}
}
}
return d[m-1][n-1];
}
代码3:改进使空间复杂度降为o(n)
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
if(obstacleGrid.empty() || obstacleGrid[0].empty()) return 0;
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
vector<long> d(n);
int i, j;
for(i = 0; i < m; i++)
{
for(j = 0; j < n; j++)
{
//如果有障碍,那肯定没有路径
if(obstacleGrid[i][j] == 1) d[j] = 0;
else
{
//如果是初始位置
if(i == 0 && j == 0) d[j] = 1;
//如果是在第一行且不是初始位置
else if( i == 0 ) d[j] = d[j-1];
//如果是i != 0 且 j != 0
else if( j != 0 ) d[j] += d[j-1];
// else if( j == 0 ) d[j] = d[j]; //如果是在第一列且不在初始位置
// else d[j] += d[j-1];
}
}
}
return d[n-1];
}






















 771
771











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








