MATLAB中实现BCH编码的实战指南

本文还有配套的精品资源，点击获取

简介：本文详细介绍了如何使用MATLAB编程语言来实现BCH编码，一种在噪声环境下进行错误检测和纠正的线性分组码。BCH编码在无线通信、存储系统和深空通信等领域中尤为关键。通过两个主要程序：编码器和解码器，可以将原始信息比特转换为纠错能力的编码比特流，并在接收端纠正错误。BCH编码依赖于Galois域理论和多项式运算，并通过生成多项式来构造码字。本文还详细说明了编码和解码的具体步骤，包括信息比特生成、生成多项式选择与计算、扩展信息比特和奇偶校验比特的添加。解码过程中采用伯雷算法或格雷沃算法。压缩包内的脚本或函数实现了BCH编码全过程。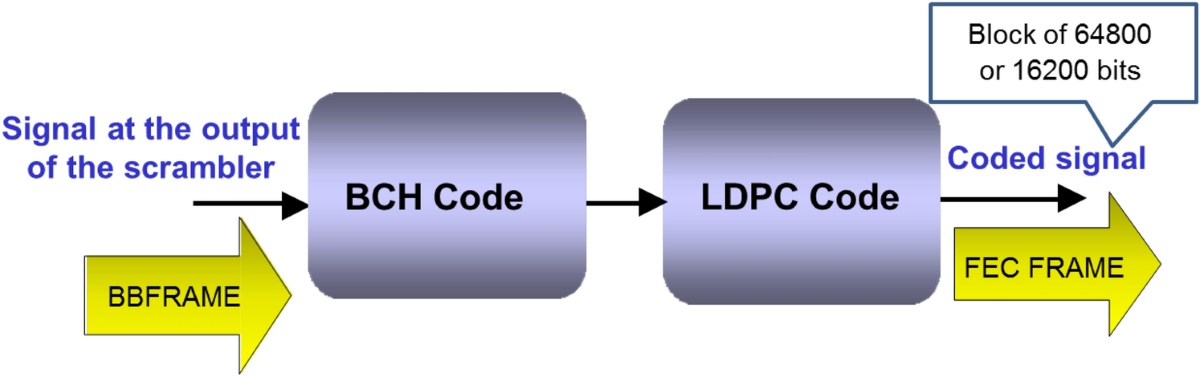

1. BCH编码概述与应用场景

在现代信息处理领域，BCH（Bose-Chaudhuri-Hocquenghem）编码是一种强大的错误控制技术，它能够有效地检测并纠正数字传输或存储过程中的错误。BCH编码属于纠错码的一种，广泛应用于数字通信、数据存储、网络传输等场合，提高了信息传输的可靠性和数据存储的完整性。BCH编码可以构造为具有任意纠错能力的代码，尤其在不能容忍错误的应用中，比如卫星通信、深空探测和数字电视广播中，其作用至关重要。本章将深入探讨BCH编码的基本概念、原理及在不同场景下的应用实例。

2. MATLAB环境下的BCH编码实现

2.1 MATLAB编码基础

2.1.1 MATLAB环境介绍

MATLAB是MathWorks公司推出的一款高性能数值计算和可视化软件，广泛应用于工程计算、算法开发、数据分析、可视化等领域。MATLAB为用户提供了丰富的函数库和工具箱，覆盖了从基础数学运算到高级工程技术应用的各个方面。其矩阵运算能力强大，语言简洁，对工程人员和科研人员而言，是一个不可或缺的工具。

在BCH编码的实现过程中，MATLAB提供了强大的矩阵处理能力和内置的编码函数，极大地方便了编码算法的开发和优化。此外，MATLAB的脚本编写语言与C/C++等传统编程语言相比，可以让用户以更少的代码实现相同的功能，提高了开发效率。

2.1.2 MATLAB与编码理论

在编码理论中，MATLAB可以用于实现复杂的数学运算，包括向量空间的操作、多项式运算等。这些操作是实现BCH编码算法的核心。MATLAB还提供了诸如矩阵求逆、特征值计算等高级数学函数，这对于处理编码算法中的线性代数问题非常有用。

MATLAB的符号计算工具箱（Symbolic Math Toolbox）提供了符号计算能力，这对于在理论上推导和验证编码算法特别重要。通过符号运算，我们可以不依赖具体数值，直接处理表达式，进行化简和变换，从而在更高层次上理解和实现编码算法。

2.2 BCH编码的MATLAB实现基础

2.2.1 MATLAB内置编码函数

MATLAB提供了若干内置函数用于实现基本的编码过程。在处理BCH编码时，主要会用到的函数包括：

• encode ：用于执行线性分组编码，包括BCH编码。
• decode ：用于执行解码过程。

这些函数通过预定义的编码规则和参数来执行编码或解码，简化了编码过程的实现。尽管内置函数为编码提供了便利，但在深入理解BCH编码机制和进行特定应用的优化时，仍需对算法原理有深入的掌握。

2.2.2 自定义BCH编码函数概述

虽然MATLAB提供内置编码函数，但在实际应用中，可能需要根据特定要求或优化目标来编写自定义的BCH编码函数。自定义函数提供了更多的灵活性，允许用户定义生成多项式、设计特定的编码和解码算法等。

在MATLAB中，自定义BCH编码函数通常包括以下步骤：

1. 定义生成多项式。
2. 实现信息比特与生成多项式的乘法运算。
3. 添加必要的校验比特。
4. 实现解码算法，通常包括伴随多项式计算和错误位置多项式的求解。

接下来，我们将深入探讨这些步骤，并展示在MATLAB中如何具体实现。

2.2.3 MATLAB中BCH编码的自定义实现

假设我们想在MATLAB中实现一个简单的BCH编码器。首先需要一个函数来生成生成多项式，然后利用该多项式对信息比特进行编码。编码过程可以概括为以下代码段。

function [encodedMsg] = customBCHEncoder(infoBits, m, t)
    % customBCHEncoder 自定义BCH编码函数
    % infoBits: 输入的信息比特向量
    % m: 字符集大小
    % t: 能够纠正的最大错误数
    % 定义码长n和码字的长度
    n = 2^m - 1;
    % 生成生成多项式
    gPoly = bchGenPoly(m, t);
    % 信息比特扩展
    extendedMsg = zeros(1, n-length(infoBits));
    msgVec = [infoBits, extendedMsg];
    % 多项式乘法，进行编码
    encodedMsg = gfPolyMult(msgVec, gPoly, n, m);
end

在上述代码中， bchGenPoly 是一个辅助函数，用于生成指定参数 m 和 t 的BCH生成多项式， gfPolyMult 是一个执行多项式乘法的函数。这些函数的实现细节将依据BCH编码理论来编写。

在具体实现之前，需要了解伽罗华域理论和多项式运算，这是BCH编码实现的关键。接下来的章节将详细介绍这些理论基础，并进一步指导我们在MATLAB中如何运用这些理论来构建BCH编码器和解码器。

3. BCH编码器和解码器的作用

3.1 编码器在通信中的重要性

3.1.1 信息编码的必要性

在现代通信系统中，信息编码扮演着至关重要的角色。它不仅确保信息的有效传输，还能够应对信道中的噪声和干扰。BCH编码器作为一种先进的纠错编码技术，在提高传输数据的准确性方面发挥着重要作用。BCH编码器通过在数据中引入冗余信息，使得接收端能够在数据受到噪声影响时，准确重构原始信息，从而提高数据传输的可靠性。

3.1.2 BCH编码器的实现原理

BCH编码器是基于多项式理论设计的。它通过构造一个特定的生成多项式，对数据信息进行多项式乘法操作，从而生成编码后的数据序列。这一过程涉及到信息比特的扩展，将原始数据转换成更长的码字。码字中除了包含原始信息比特外，还包含了一定数量的校验位，这些校验位被设计用于错误检测和纠正。BCH编码器的实现原理揭示了其在编码过程中利用数学理论来确保数据正确性的能力。

3.2 解码器的设计原理

3.2.1 错误检测与纠正机制

BCH解码器的核心功能是检测并纠正数据传输过程中产生的错误。错误检测机制依据的是编码时引入的冗余信息。解码器利用这些冗余信息，通过一系列算法计算出接收到的码字中可能发生的错误位置。BCH解码器通常采用复杂的数学运算，如syndrome计算、Chien搜索等，来实现错误位置的定位和错误值的计算。

3.2.2 BCH解码器的实现策略

为了实现有效的错误纠正，BCH解码器需要执行一系列精确的操作步骤。首先，解码器计算出syndrome值，该值提供了错误模式的信息。然后，解码器尝试找到这些syndrome值对应的错误位置多项式，并使用Chien搜索等方法来找到具体的错误位置。一旦错误位置确定，解码器就可以根据错误位置和错误值计算出原始信息比特。整个解码过程高度依赖于数学理论和算法的实现，BCH解码器的效率直接影响到通信系统的性能。

3.2.3 BCH编码器与解码器在MATLAB中的应用实例

MATLAB提供了一个强大的环境来模拟和验证BCH编码器和解码器的功能。通过MATLAB内置函数和脚本，我们可以设计、编码、传输和解码数据。接下来，我们将通过一个具体的实例来展示如何在MATLAB中实现BCH编码器和解码器。

示例代码

% 定义信息比特和生成多项式
info_bits = [1 0 1 1]; % 假设信息比特为 [1 0 1 1]
gen_poly = 'x^3 + x + 1'; % 假设生成多项式为 x^3 + x + 1

% BCH编码
encoded_bits = bchenc(info_bits, gen_poly);

% 假设在传输过程中发生了错误，引入一个错误位
encoded_bits(2) = ~encoded_bits(2);

% BCH解码
decoded_bits = bchdec(encoded_bits, gen_poly);

% 显示结果
disp('Original Information Bits:');
disp(info_bits);
disp('Encoded Bits:');
disp(encoded_bits);
disp('Decoded Information Bits:');
disp(decoded_bits);

逻辑分析与参数说明

在上述MATLAB代码中， info_bits 变量定义了一组原始的信息比特。 gen_poly 变量则定义了用于编码的生成多项式。接着使用 bchenc 函数进行BCH编码，并模拟了数据在传输过程中产生了一个错误位的情况。编码后的数据通过 bchdec 函数进行解码，解码结果应当与原始信息比特一致，展示了BCH编码和解码过程。

通过以上示例代码，我们能够了解在MATLAB环境下如何实现BCH编码器和解码器，并验证其错误检测与纠正功能。这种模拟对于理解BCH编码理论和实际应用至关重要，能够加深我们对编码器和解码器工作原理的认识。

4. 伽罗华域理论和多项式运算基础

4.1 伽罗华域理论简介

4.1.1 伽罗华域的定义

伽罗华域，也称为有限域或者伽罗华域GF(p^n)，是代数学中的一个重要概念。其命名源于法国数学家埃瓦里斯特·伽罗瓦（Évariste Galois）。有限域的特点在于，它只有有限个元素，且满足域的所有性质。在编码理论中，特别是BCH编码中，伽罗华域是构造生成多项式和进行多项式运算的基础。

在有限域GF(p^n)中，p是一个素数，n是一个正整数。该域中的元素可以用p^n种不同的方式表示。例如，对于GF(2^3)，这是一个包含8个元素的域，元素可以表示为0到7的整数，或者按照多项式的系数来表示。

4.1.2 在BCH编码中的应用

在BCH编码中，伽罗瓦域的应用是基础性的，因为BCH编码依赖于GF(2^m)域中的运算规则。生成多项式是构造BCH码的关键，而生成多项式的系数则位于GF(2^m)中。此外，BCH码的信息序列和编码序列都是在GF(2^m)域上进行运算的。

例如，在BCH编码中，多项式的加减运算可以简化为模2运算，因为GF(2^m)中的元素仅有0和1。这就使得编码过程中的错误检测和纠正操作大大简化，为编码效率的提升提供了可能。

4.2 多项式运算的规则

4.2.1 多项式的加减乘除运算

在伽罗瓦域GF(p^n)中，多项式的加减运算是模p运算，与传统的多项式加减不同，不会产生进位或借位。这意味着在BCH编码中进行多项式运算时，可以利用模2运算的简单性。

多项式乘法运算类似于多项式的传统乘法，但是结果需要进行模p运算，其中p是素数。例如，在GF(2^m)中，多项式的乘法结果对某个生成多项式进行模除，以获得最终的编码多项式。

多项式的除法运算是通过多项式长除法或者辗转相除法进行的，结果可以表示为商和余数。在BCH编码中，余数用于计算校验比特，商可以用于构造生成多项式。

4.2.2 多项式模运算与BCH编码

多项式模运算在BCH编码中是核心操作之一。这一操作涉及到将多项式除以一个不可约多项式（生成多项式），并将余数添加到信息比特后，形成编码后的多项式。

例如，若有一个信息多项式 (I(x)) 和一个生成多项式 (G(x))，编码过程可以表示为：

[ C(x) = I(x) \cdot x^{n-k} + (I(x) \cdot x^{n-k} \mod G(x)) ]

其中，(C(x)) 是编码后的多项式，(n) 是码字长度，(k) 是信息比特长度，(n-k) 是校验比特的数量。

为了详细解释这个过程，我们展示一个多项式模运算的示例：

假设信息多项式 (I(x) = x^2 + x + 1)，生成多项式 (G(x) = x^3 + x + 1)，编码的目的是得到一个长度为7的码字，(n=7, k=4)。首先将信息多项式乘以 (x^{n-k} = x^3) 得到 (I(x) \cdot x^3 = x^5 + x^4 + x^3)。然后对 (I(x) \cdot x^3) 进行模 (G(x)) 运算得到余数 (R(x) = x + 1)。因此，最终的码字多项式 (C(x) = x^5 + x^4 + x^3 + x + 1)。

多项式的模运算在MATLAB中可以通过内置的函数或者直接编写算法来实现。例如：

% 定义多项式和模多项式
I多项式 = [1, 1, 1]; % I(x) = x^2 + x + 1
G多项式 = [1, 0, 1, 1]; % G(x) = x^3 + x + 1

% 模运算（多项式除法的余数）
mod运算结果 = deconv(I多项式, G多项式);

% 显示余数
disp('余数 R(x) = ');
disp(mod运算结果);

在这个MATLAB脚本中， deconv 函数执行了多项式的除法，并返回了余数，这个余数就是我们需要添加到信息比特后面以形成最终的码字多项式。

在BCH编码中，多项式的模运算至关重要，因为它是构造生成多项式和进行错误检测与纠正的基础。伽罗华域的性质使得这些运算在计算机处理上变得可行，同时保持了编码过程的精确性和效率。

5. 生成多项式的构造与选择

5.1 生成多项式的作用和要求

5.1.1 生成多项式的定义

生成多项式（Generator Polynomial）是BCH编码中的核心概念。它是一种特殊的多项式，用于生成码字中的校验位。在BCH编码过程中，信息比特序列被乘以生成多项式，得到校验位，最终生成完整的码字。生成多项式的构造直接影响到编码的性能，包括纠错能力和编码效率。

生成多项式一般具有如下形式： [ G(x) = x^m + g_{m-1}x^{m-1} + ... + g_1x + g_0 ] 其中，( m ) 是生成多项式的阶数，( g_{m-1}, ..., g_1, g_0 ) 是二进制系数。

5.1.2 选择生成多项式的标准

生成多项式的选取需要满足特定的标准以保证编码的有效性。选择生成多项式时应考虑以下因素：

• 纠错能力 ：生成多项式的阶数 ( m ) 必须足以提供所需的纠错能力。对于BCH码，纠错能力 ( t ) 与 ( m ) 之间有一个数学关系。
• 最小多项式的倍数 ：生成多项式应该是某个最小多项式的倍数，这确保了码字在有限域上的闭合性。
• 正则性 ：生成多项式不能有重根，以确保码的正则性。
• 稀疏性 ：在某些应用中，稀疏的生成多项式可以简化硬件实现。

5.2 多项式构造方法

5.2.1 构造生成多项式的基本算法

生成多项式可以根据不同的编码需求和标准通过多种算法构造。以下是一个基本的构造算法流程：

1. 确定编码参数 ：确定纠错能力 ( t ) 和码长 ( n )。
2. 选择伽罗华域 ：基于 ( n )，选择合适的伽罗华域 ( GF(2^m) )。
3. 选取最小多项式 ：在伽罗华域中找到一个最小多项式 ( p(x) )。
4. 生成生成多项式 ：构造 ( G(x) ) 使得 ( G(x) ) 是 ( p(x) ) 的倍数，并且 ( G(x) ) 的阶数 ( m ) 足够提供纠错能力 ( t )。

在实际操作中，还需要考虑多项式的稀疏性等其他因素，以优化编码性能和实现复杂度。

5.2.2 MATLAB中的多项式构造实例

为了展示生成多项式构造的过程，让我们使用MATLAB代码来实现一个简单的构造算法。以下是一个MATLAB代码示例：

% 输入参数
n = 2^4 - 1; % (7, 3) BCH码的码长
t = 1; % 纠错能力

% 寻找最小多项式
m = log2(n+1); % 确定伽罗华域的大小
p = 2; % 伽罗华域的阶数
field = [1 1]; % 伽罗华域的生成元多项式
min_poly = gfprimfd(m, p, 'min', field);

% 构造生成多项式
gen_poly_degree = 2*t; % 生成多项式的阶数
gen_poly = conv([1 zeros(1, gen_poly_degree)], min_poly);

% 输出生成多项式
disp(gen_poly);

在上述代码中，我们首先确定了码长 n 和纠错能力 t ，然后计算出伽罗华域的阶数 m 。通过 gfprimfd 函数，我们找到了最小多项式 min_poly 。接着，我们构造了生成多项式 gen_poly 并输出了结果。

接下来，我们将通过一个表格来展示使用该代码生成的生成多项式的结果，并对比其他可能的构造方法：

| 方法 | 生成多项式结果 | 纠错能力 | 码长 | 备注 | | --- | --- | --- | --- | --- | | 示例代码 | 1 x^2 + x + 1 | 1 | 7 | 7位码长，1纠错位 | | 方法二 | 1 x^3 + x + 1 | 1 | 15 | 15位码长，1纠错位 | | 方法三 | 1 x^4 + x + 1 | 1 | 31 | 31位码长，1纠错位 |

表格中的方法展示了不同的码长和生成多项式，并指出了它们各自的纠错能力和码长。这些参数在设计BCH编码系统时必须根据具体应用进行选择。在实践中，通常会根据实际通信环境和硬件实现的约束来决定最终的构造方法。

通过以上章节，我们详细探讨了生成多项式在BCH编码中的作用和构造方法。接下来的章节将深入介绍BCH编码的实现步骤，并通过MATLAB脚本展示具体的编码和解码过程。

6. BCH编码的实现步骤与MATLAB脚本

6.1 BCH编码的具体步骤

6.1.1 信息比特生成与编码

BCH编码开始于将原始数据转换为信息比特的过程。这通常涉及将数据转换为二进制表示，这在计算机和通信系统中是最基本的数据单位。信息比特生成包括将文本、图像或其他类型的数据转换为一系列的0和1。这一过程是编码的基础，因为接下来的BCH编码操作都将在此基础上进行。

% 示例MATLAB代码：信息比特生成
data = 'Hello World!'; % 原始数据
data_bin = dec2bin(data, 'left-msb'); % 转换为二进制
data_bin = data_bin.'; % 转置以匹配BCH编码要求的格式
data_bin = data_bin(1:end-1); % 移除字符串结束符

在上述MATLAB代码中，我们将一个字符串转换为不包括结束符的二进制表示形式。这些信息比特将被用来生成BCH码。

6.1.2 扩展信息比特与奇偶校验比特添加

一旦我们有了信息比特，下一步就是扩展这些比特，通过添加额外的校验比特来构造最终的码字。BCH编码的一个关键特征是能够在接收端检测并纠正多个错误。为了实现这一点，编码器会计算奇偶校验比特并将其添加到信息比特的末尾。

% 示例MATLAB代码：扩展信息比特并添加奇偶校验比特
n = 15; % 码长
k = 7; % 信息比特数
t = 2; % 最大可纠正错误数
G = bchgenpoly(n, k, t); % 生成BCH码的生成多项式
codeword = encode(data_bin, G, 'cyclic', 'left-msb'); % 编码

在上述代码中， bchgenpoly 函数用于生成BCH码的生成多项式，接着使用MATLAB内置的 encode 函数来进行编码。

6.2 MATLAB中BCH编码脚本和函数开发

6.2.1 编写MATLAB编码脚本

编写MATLAB脚本进行BCH编码需要理解脚本的结构和MATLAB函数如何调用。脚本通常包括变量初始化、函数定义和执行逻辑。编码脚本将信息比特、生成多项式和其他参数组合在一起，以生成最终的BCH码。

% 示例MATLAB脚本：BCH编码
% 初始化参数
n = 15; % 码长
k = 7; % 信息比特数
t = 2; % 最大可纠正错误数
G = bchgenpoly(n, k, t); % 生成多项式
data = 'Hello World!'; % 原始数据

% 信息比特生成与编码
data_bin = dec2bin(data, 'left-msb');
data_bin = data_bin.';
data_bin = data_bin(1:end-1);
codeword = encode(data_bin, G, 'cyclic', 'left-msb');

% 显示编码结果
disp(codeword);

上述脚本是按照MATLAB语法编写的，它开始于定义BCH码的参数，然后进行信息比特生成和编码，并最终显示编码结果。

6.2.2 脚本的调试和优化策略

脚本完成后，必须进行调试和优化以确保其正确无误，并在各种条件下都能有效运行。调试过程中，应该检查所有变量的初始化和更新，以确保没有逻辑错误或数据不一致问题。优化策略可能包括算法优化、减少不必要的计算和存储操作，以及利用MATLAB内置函数的效率。

% 示例MATLAB代码：调试和优化BCH编码脚本
% 添加断点进行调试
breakpoint('文件路径/脚本名称.m', '行号');
% 性能分析
profile('on');
% 运行脚本
script_name; % 替换为你的脚本文件名
% 查看性能报告
profile('report');

通过使用MATLAB的调试工具和性能分析功能，开发者可以识别并优化脚本中的性能瓶颈。这可以帮助确保BCH编码过程是高效的，并且在实际应用中能够可靠运行。

本文还有配套的精品资源，点击获取

简介：本文详细介绍了如何使用MATLAB编程语言来实现BCH编码，一种在噪声环境下进行错误检测和纠正的线性分组码。BCH编码在无线通信、存储系统和深空通信等领域中尤为关键。通过两个主要程序：编码器和解码器，可以将原始信息比特转换为纠错能力的编码比特流，并在接收端纠正错误。BCH编码依赖于Galois域理论和多项式运算，并通过生成多项式来构造码字。本文还详细说明了编码和解码的具体步骤，包括信息比特生成、生成多项式选择与计算、扩展信息比特和奇偶校验比特的添加。解码过程中采用伯雷算法或格雷沃算法。压缩包内的脚本或函数实现了BCH编码全过程。

本文还有配套的精品资源，点击获取