Hopfield网络在解决TSP问题中的VC++算法实现

本文还有配套的精品资源，点击获取

简介：Hopfield网络是一种模拟神经元交互的人工神经网络模型，用于解决旅行商问题（TSP），这是一个NP完全问题。本文介绍如何通过VC++实现Hopfield网络算法，包括权重初始化、状态更新、能量计算等步骤，来寻找TSP的近似解。实现过程中可能会遇到局部最小值问题，因此需要采取策略来提高解的质量。通过本项目，读者可以加深对Hopfield网络和优化算法的理解，并学会如何将理论应用到实际代码中。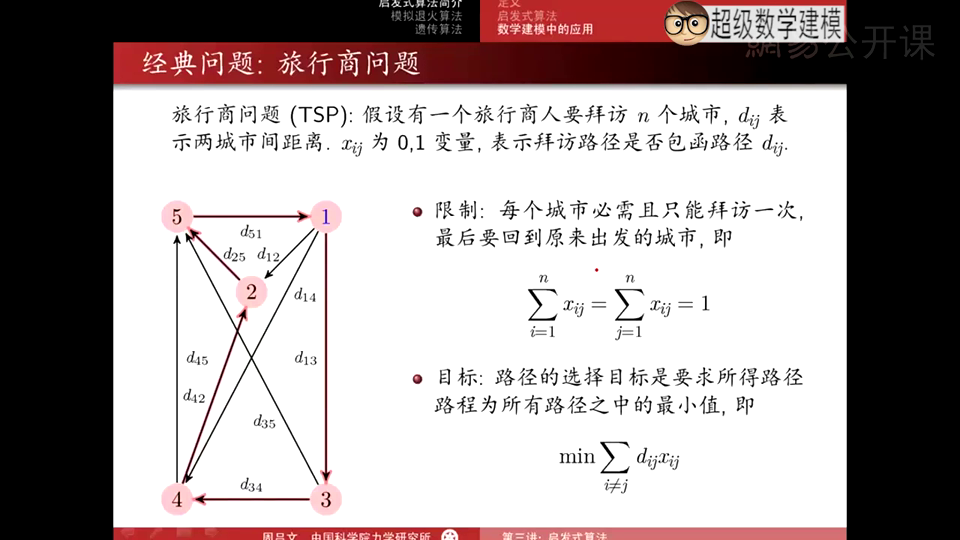

1. Hopfield网络介绍

Hopfield网络是一种反馈型神经网络，由美国物理学家John Hopfield于1982年提出。与传统的前馈神经网络不同，Hopfield网络中的神经元是全连接的，并且网络是动态的，能够通过调整自身状态来达到能量最小化。这种网络在解决优化问题，比如旅行商问题（TSP）中，表现出强大的潜能。本章将带您了解Hopfield网络的基本概念，其工作原理和应用场景，为后续章节中关于TSP问题的具体应用打下基础。

神经网络的基本组成单元

Hopfield网络由简单的神经元组成，每个神经元都能够处于开（1）或关（-1）两种状态。神经元之间的连接是全连接的，即每个神经元都与其他所有神经元相连。网络中没有输入层和输出层之分，所有神经元参与信息处理。

Hopfield网络的动态特性和能量函数

Hopfield网络的最大特点是其动态演化过程遵循能量函数的最小化原则。网络从任一初始状态出发，通过更新神经元的状态，不断降低能量函数值，直至找到稳定的能量极小点。能量函数是衡量网络状态优劣的标准，其值越低，表示网络状态越稳定，离最优解越近。

2. 旅行商问题（TSP）概念

2.1 TSP问题的基本定义和数学模型

2.1.1 TSP问题的定义和应用场景

旅行商问题（Traveling Salesman Problem, TSP）是组合优化中的一个经典问题，属于NP-hard（非确定性多项式时间困难）类问题。它描述的是这样一个场景：一个旅行商希望从一个城市出发，经过一系列城市一次且仅一次后，再回到原出发点，并且希望所走的路径总距离最短。

TSP问题不仅在理论研究上具有重要意义，它同样广泛地应用于物流配送、电路板设计、DNA序列分析、工业生产等实际领域。例如，在物流配送中，TSP问题可以帮助企业规划出最佳的配送路线，从而最小化运输成本和时间。在电路设计中，TSP问题可以被用来寻找最小化布线长度的路径。

2.1.2 TSP问题的数学表示和特点

从数学角度来看，TSP问题可以被定义为一个带权完全图，其中每个顶点代表一个城市，边的权重代表城市间的距离。问题的目标是找到一条总权重最小的哈密顿回路，即经过每个顶点恰好一次并回到起点的闭合路径。

TSP问题的特点主要包括：

• 组合爆炸 ：随着城市数量的增加，可能的路径组合数量呈指数级增长，这使得暴力搜索算法在城市数量较多时变得不切实际。
• NP-hard特性 ：目前没有已知的多项式时间复杂度的算法可以解决所有TSP问题实例，因此寻找近似解或启发式解是常见的解决办法。
• 优化目标多样性 ：虽然经典TSP的优化目标是最小化路径长度，但在实际应用中，可能会有诸如最小化时间、成本等其他优化目标。

2.2 TSP问题的求解方法概述

2.2.1 经典算法：动态规划与分支限界

对于TSP问题的求解，存在多种算法策略，其中最著名的有动态规划和分支限界法。

动态规划（Dynamic Programming, DP） 是通过将大问题分解为小问题，并使用一个表格记录子问题的解，以避免重复计算。动态规划方法尤其适合解决具有“重叠子问题”和“最优子结构”性质的问题。对于TSP问题，这意味着可以找到比暴力搜索更高效的算法。

动态规划解决TSP问题的基本思路是，首先确定路径的起始城市，然后按照旅行顺序逐步计算到达每个城市的最短路径，直至最后返回起始城市。在每一步中，都选择下一个城市使总路径长度最短。

动态规划方法的时间复杂度是指数级的，但比暴力搜索方法要好，特别是当城市数量较少时。然而，对于大规模TSP问题，动态规划所需的空间复杂度可能会变得非常大。

分支限界法（Branch and Bound） 是一种用来解决整数规划问题的通用策略，它通过探索树形结构的解空间，并通过界限函数剪枝，避免搜索过多无用的路径。分支限界法在求解TSP问题时，会构建一棵搜索树，其中每一个节点代表一个子问题。算法会尝试为每个子问题生成两个或多个子问题，并在搜索树中进行分支。对于TSP问题，界限函数通常是已走路径的长度与剩余距离的下界之和，这个下界可以通过一些高效的近似算法来估计。

2.2.2 启发式算法：遗传算法与蚁群算法

鉴于TSP问题的NP-hard特性，对大规模问题实例，经典算法常常无法在合理时间内求得精确解。因此，启发式算法，如遗传算法和蚁群算法，被提出用来获得问题的近似解或启发式解。

遗传算法（Genetic Algorithm, GA） 是受自然选择机制启发而产生的搜索算法。它通过模拟生物进化的过程，迭代地改进一组候选解。对于TSP问题，每一个候选解对应一条可能的路径。在每一代中，会根据路径长度（适应度）选择较好的路径，通过交叉和变异操作产生新的路径。遗传算法的优点是能快速地接近最优解，但通常无法保证找到全局最优解。

蚁群算法（Ant Colony Optimization, ACO） 是模拟蚂蚁寻找食物路径的行为而设计的算法。在TSP问题中，蚂蚁代表不同的路径，每只蚂蚁通过“信息素”来标记路径。信息素的浓度会随着时间增长而增加，从而吸引其他蚂蚁沿着这些路径移动。蚂蚁在移动过程中会根据路径的长度和信息素浓度来更新信息素，最终导致较短的路径上的信息素浓度更高，从而被更多的蚂蚁选择。随着时间的推移，蚁群算法能较好地收敛到较优的路径。

接下来，我们将探讨如何使用VC++实现Hopfield网络，并进一步讨论权重矩阵的初始化方法。这将为理解TSP问题与神经网络之间的关联以及实际应用打下基础。

3. VC++中Hopfield网络的实现

Hopfield网络是一种递归神经网络，具有能量函数和动态特性，能够实现模式存储和优化计算。本章节将详细介绍Hopfield网络的结构和工作原理，以及如何在VC++中实现该网络。

3.1 Hopfield网络的结构和工作原理

3.1.1 神经网络的基本组成单元

Hopfield网络由多个相互连接的神经元组成，每个神经元具有二进制状态（-1或+1），通过加权连接与其他神经元相连。神经元的输入是来自其他神经元的加权信号和自身的阈值，输出是根据输入信号和当前状态计算得出的更新状态。

为了更好地理解Hopfield网络，我们可以借助以下公式描述神经元的输入和输出关系：

h_i(t) = ∑(w_ij * s_j(t)) - θ_i
s_i(t+1) = f(h_i(t))

这里， s_i(t) 表示第 i 个神经元在时间 t 的状态， w_ij 表示神经元 i 和神经元 j 之间的连接权重， θ_i 是神经元 i 的阈值， h_i(t) 是神经元 i 在时间 t 的总输入， f 是传递函数（通常使用符号函数）。

3.1.2 Hopfield网络的动态特性和能量函数

Hopfield网络通过迭代的方式更新神经元的状态，直至网络达到稳定状态。这种动态特性的关键在于网络具有能量函数，它随着网络状态的演化而降低，直到找到能量最低的状态，此时网络被认为达到了平衡。

能量函数通常定义为：

E = -(1/2) * ∑∑(w_ij * s_i * s_j) - ∑(θ_i * s_i) + ∑(h_i * log(1 + exp(-h_i)))

其中， E 是网络的能量，第一项表示所有神经元之间的连接权重和状态的乘积的总和，第二项是神经元阈值和状态的乘积的总和，第三项是为了数学上的连续性和平滑性而引入的项。

能量函数有助于理解网络的稳定性和演化过程，因为每一步状态更新都会导致能量的减少，直到找到稳定点，能量函数不再改变。

3.2 Hopfield网络的编程实现步骤

3.2.1 创建神经网络类和数据结构

在VC++中，实现Hopfield网络的第一步是定义所需的类和数据结构。我们首先定义 Neuron 类来表示单个神经元，然后定义 HopfieldNetwork 类来管理整个网络。

class Neuron {
public:
    int state; // 神经元当前状态
    float threshold; // 神经元阈值
    // ... 其他成员变量和方法
};

class HopfieldNetwork {
private:
    vector<Neuron> neurons; // 存储神经元的数组
    vector<vector<float>> weights; // 权重矩阵
    int numNeurons; // 神经元数量
public:
    HopfieldNetwork(int numNeurons); // 构造函数
    void InitializeNetwork(); // 初始化网络
    void UpdateStates(); // 更新神经元状态
    float ComputeEnergy(); // 计算能量
    // ... 其他成员函数
};

3.2.2 实现网络的初始化和状态更新函数

初始化是网络搭建的关键步骤。我们需要初始化神经元的阈值和权重矩阵。权重矩阵通常是对称的，且对角线元素是0。

void HopfieldNetwork::InitializeNetwork() {
    // 初始化权重矩阵和神经元
    // 示例代码省略具体的初始化逻辑
    // ...
}

状态更新函数用于迭代更新网络中每个神经元的状态。这是通过计算每个神经元的总输入，然后应用传递函数来实现的。

void HopfieldNetwork::UpdateStates() {
    for (auto& neuron : neurons) {
        float totalInput = 0.0f;
        for (size_t i = 0; i < numNeurons; ++i) {
            totalInput += weights[neuron.id][i] * neurons[i].state;
        }
        totalInput -= neuron.threshold; // 调整阈值项
        // 应用传递函数，更新状态
        neuron.state = (totalInput > 0) ? 1 : -1;
    }
}

以上代码展示了如何使用权重矩阵和神经元状态来更新网络中每个神经元的状态。需要注意的是，这个更新过程需要在一个循环中不断地执行，直到网络稳定或达到预定的迭代次数。

通过上述步骤，我们可以在VC++中实现一个基本的Hopfield网络模型。接下来的章节将会进一步探讨网络的优化、调试以及如何与特定问题（例如TSP问题）相结合以求解。

4. 权重矩阵初始化方法

4.1 权重矩阵初始化的重要性

权重矩阵是Hopfield网络中的核心概念之一，它决定了网络中的神经元如何相互作用。初始化权重矩阵的策略直接影响到网络的性能和最终解的质量。合适的权重矩阵可以使网络更快地收敛到稳定状态，并提高求解问题的准确性。

4.1.1 合适权重矩阵对网络性能的影响

权重矩阵的初始化需要确保网络能够快速且有效地学习到输入模式。如果权重矩阵初始化不当，可能会导致网络收敛速度慢、陷入局部最小值或者不能稳定到任何一个有效的解。此外，权重矩阵的初始化还会影响网络的存储容量，即网络能记住多少个模式的能力。

4.1.2 权重矩阵初始化的常见策略

初始化权重矩阵有多种方法，常见策略包括： - 随机初始化：权重矩阵中的值随机赋予小的数值，通常是正负之间的随机数。 - 对称初始化：权重矩阵是对称的，即 (W_{ij} = W_{ji})，这有助于保证能量函数的稳定性。 - 基于Hebb规则的初始化：根据Hebb学习规则，如果两个神经元同时激活，它们之间的权重应当加强。权重矩阵 (W_{ij}) 的值通常根据输入模式的共激活情况来设置。

4.2 从TSP到权重矩阵的映射

旅行商问题（TSP）是一个经典的优化问题，其核心是如何找到一条最短的路径，让旅行商经过一系列城市且每个城市只访问一次后回到起点。通过将TSP问题转化为Hopfield网络，可以利用神经网络的模式识别和优化特性来求解TSP。

4.2.1 TSP约束条件转化为权重矩阵

TSP问题中的约束条件，例如每个城市只能访问一次，可以转化为权重矩阵中的惩罚项。这些惩罚项保证了网络状态更新时会考虑到TSP问题的约束，从而避免生成无效解。

4.2.2 权重矩阵的计算示例和分析

例如，假设有一个简单的TSP问题包含3个城市，我们可以设定一个3x3的权重矩阵 (W)，其对角线元素为0，其余元素为负值（表示惩罚），具体值取决于城市间距离。初始状态可以设置为一个随机状态，表示旅行商访问城市的初始顺序。

|   | City1 | City2 | City3 |
|---|-------|-------|-------|
|City1|   0   | -10   | -15   |
|City2| -10   |   0   | -12   |
|City3| -15   | -12   |   0   |

在上表中，-10和-12表示的是旅行商从城市2到城市1和城市3的惩罚值，15和12表示的是城市1到城市3和城市2的惩罚值。通过调整权重值，我们可以控制网络在迭代过程中倾向于选择更短的路径。

在实际编程实现时，我们首先需要构建一个完整的权重矩阵，将所有的城市和城市间距离编码到矩阵中。接着，通过一系列的迭代更新过程，网络将逐渐收敛到一个稳定状态，该状态对应的路径接近于TSP问题的最优解。

权重矩阵的初始化和计算是整个Hopfield网络求解TSP问题的关键步骤。后续章节将详细介绍如何在VC++中实现权重矩阵的初始化以及如何进行网络迭代更新。

5. 神经元状态的初始化和更新

5.1 神经元状态初始化的方法和原则

在Hopfield网络中，神经元的状态通常由二进制值表示，即每个神经元的状态为+1或-1。合理的初始化神经元状态对于网络能否快速收敛到稳定状态至关重要。

5.1.1 初始状态的随机性和合理性

初始化神经元状态时，可以根据问题的特定背景来决定是选择完全随机的初始状态还是基于某种规则的初始状态。通常，随机初始化可以避免算法陷入某个特定的局部最小值，但是可能需要更多的迭代次数才能找到全局最小值。

#include <vector>
#include <cstdlib>
#include <ctime>

// 初始化神经元状态为随机值
void initialize_neuron_states(std::vector<int>& states, size_t neuron_count) {
    srand(time(NULL));  // 设置随机种子
    for (size_t i = 0; i < neuron_count; ++i) {
        // 随机生成-1或+1
        states[i] = rand() % 2 ? 1 : -1;
    }
}

int main() {
    size_t neuron_count = 10;  // 假设网络有10个神经元
    std::vector<int> states(neuron_count);  // 创建状态向量

    initialize_neuron_states(states, neuron_count);  // 初始化神经元状态

    // 输出初始化后的状态
    for (auto state : states) {
        std::cout << state << " ";
    }
    std::cout << std::endl;

    return 0;
}

在上述代码中， initialize_neuron_states 函数用于初始化神经元状态。它接受一个整数向量的引用和神经元的数量作为参数。通过 rand() 函数生成随机数，并基于其奇偶性决定神经元的状态为-1或+1。

5.1.2 神经元状态更新的基本规则

神经元状态的更新通常遵循“赢者通吃”的原则，即每个神经元根据其他所有神经元的状态来更新自己的状态。如果一个神经元的状态与其他神经元状态的乘积之和大于零，那么这个神经元的状态将变为+1；否则，变为-1。这个过程可以通过以下步骤描述：

1. 计算每个神经元的输入，即当前所有神经元状态的加权和。
2. 如果输入为正数，则神经元状态更新为+1；如果为负数，则更新为-1。

// 根据权重矩阵和当前状态更新神经元状态
void update_neuron_states(std::vector<int>& states, const std::vector<std::vector<double>>& weight_matrix) {
    std::vector<int> new_states(states.size());
    for (size_t i = 0; i < states.size(); ++i) {
        double sum = 0.0;
        for (size_t j = 0; j < states.size(); ++j) {
            sum += weight_matrix[i][j] * states[j];
        }
        new_states[i] = (sum > 0) ? 1 : -1;
    }
    states = new_states;
}

在 update_neuron_states 函数中，我们计算了每个神经元的输入和，并根据和的正负来更新状态。

5.2 神经元状态的动态演化过程

神经元状态的动态演化过程描述了网络是如何从初始状态演化到最终稳定状态的。

5.2.1 神经元状态更新的实现细节

在Hopfield网络的模拟实现中，神经元状态的更新通常是在一个循环中进行的，直到网络达到一个稳定状态或者达到预定的迭代次数。

// 模拟神经元状态的动态演化过程
void simulate_neuron_evolution(std::vector<int>& states, const std::vector<std::vector<double>>& weight_matrix, size_t max_iterations) {
    for (size_t iteration = 0; iteration < max_iterations; ++iteration) {
        update_neuron_states(states, weight_matrix);  // 更新状态

        // 输出每一步的迭代状态
        for (auto state : states) {
            std::cout << state << " ";
        }
        std::cout << std::endl;

        // 检查是否达到稳定状态
        // 这里可以添加代码以检查状态是否稳定并相应地停止迭代
    }
}

在 simulate_neuron_evolution 函数中，我们使用一个 for 循环来重复更新神经元状态的步骤。通过设置 max_iterations 参数来控制最大迭代次数，以防止算法运行时间过长。

5.2.2 状态演化过程的可视化和解释

通过可视化神经元状态随时间变化的过程，可以更容易地理解网络是如何工作的。在VC++中，可以使用MFC（Microsoft Foundation Classes）或者第三方图形库来绘制状态变化的图表。

// 假设我们有一个MFC应用程序
void visualize_state_evolution(CWnd* pWnd, std::vector<int>& states, const std::vector<std::vector<double>>& weight_matrix, size_t max_iterations) {
    CDC* pDC = pWnd->GetDC();  // 获取设备上下文（DC）
    int window_width = pWnd->GetClientRect().right;  // 获取窗口宽度
    int window_height = pWnd->GetClientRect().bottom;  // 获取窗口高度

    for (size_t iteration = 0; iteration < max_iterations; ++iteration) {
        update_neuron_states(states, weight_matrix);  // 更新状态

        // 清除屏幕
        pDC->FillSolidRect(0, 0, window_width, window_height, RGB(255, 255, 255));

        // 绘制状态
        int bar_width = window_width / states.size();
        int bar_height;
        for (size_t i = 0; i < states.size(); ++i) {
            bar_height = abs(states[i] * window_height / 2);  // 将状态值映射到高度
            pDC->Rectangle(i * bar_width, (window_height / 2) - bar_height, (i + 1) * bar_width, (window_height / 2) + bar_height);
        }

        // 等待一段时间后继续迭代
        Sleep(1000);  // 暂停1秒
        pWnd->UpdateWindow();  // 更新窗口以显示最新绘制的图形
    }

    pWnd->ReleaseDC(pDC);  // 释放设备上下文
}

在 visualize_state_evolution 函数中，我们首先获取MFC窗口的设备上下文，然后在每次迭代后绘制每个神经元的状态。状态以条形图的形式显示，通过条形的长度和位置来表示神经元是+1还是-1。这种方法可以直观地展示网络状态的演化过程。

接下来，将进入第六章，我们将深入了解Hopfield网络中的能量计算方式，理解能量函数在神经网络动态和稳定性的关键作用。

6. 网络能量的计算方式

6.1 能量函数的数学表达和作用

6.1.1 Hopfield网络能量函数的定义

Hopfield网络是一个可以收束到稳定状态的能量优化系统。网络的能量函数是衡量网络状态稳定性的关键指标。对于一个具有n个神经元的Hopfield网络，其能量函数E可以表示为：

[ E = -\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1, j \neq i}^{n} w_{ij} v_i v_j - \sum_{i=1}^{n} \theta_i v_i ]

其中，( w_{ij} ) 是神经元i和j之间的连接权重，( v_i ) 是神经元i的输出状态（取值通常为-1或+1），( \theta_i ) 是神经元i的阈值。

6.1.2 能量函数在网络稳定性和求解中的角色

能量函数的值随神经元状态变化而变化。在Hopfield网络中，网络会不断更新神经元的状态，直至达到一个稳定的能量最小值。在稳定状态下，能量函数值不再降低，表明网络已经收敛。因此，能量函数的最小值对应于TSP问题的一个可行解。

6.2 能量计算的编程实现

6.2.1 编写能量计算函数

在VC++中实现Hopfield网络能量计算函数可以按照以下步骤进行：

double CalculateNetworkEnergy(double** weights, int* neurons, int size) {
    double energy = 0.0;
    for (int i = 0; i < size; ++i) {
        for (int j = 0; j < size; ++j) {
            if (i != j) {
                energy -= weights[i][j] * neurons[i] * neurons[j];
            }
        }
        energy -= neurons[i] * bias[i]; // bias[i] 为神经元i的阈值乘以-1
    }
    return energy;
}

6.2.2 能量计算结果的分析和利用

计算得到的能量值是评估当前神经元状态优劣的关键指标。在TSP问题中，较低的能量值通常意味着较短的旅行路径。能量计算完成后，可以利用该结果来判断网络是否已经收敛或者是否需要继续迭代。下面是一个示例输出：

#include <iostream>

// ... (省略之前的代码)

int main() {
    // 初始化权重矩阵和神经元状态等
    // ...
    double energy = CalculateNetworkEnergy(weights, neurons, size);
    std::cout << "当前网络能量为: " << energy << std::endl;
    // 根据能量值判断是否继续迭代
    // ...
    return 0;
}

在上述代码块中， CalculateNetworkEnergy 函数通过遍历所有的神经元和它们之间的连接权重来计算当前的网络能量。完成能量计算后，可以通过输出当前能量值来进行分析，并决定是否需要继续迭代过程。一个较低的能量值表明当前解是接近全局最优解的，因此在TSP问题中，能量值可以用来评估路径的质量。

能量计算不仅对评估当前解的优劣有重要意义，而且对于整个网络的迭代和优化过程也是至关重要的。通过不断计算和比较能量值，可以帮助网络跳出局部最小值陷阱，寻找更优的全局解。

7. 迭代停止条件与结果解析

7.1 迭代停止的条件和判断方法

在神经网络，尤其是Hopfield网络中，迭代过程是寻找稳定状态的关键。停止迭代的条件决定了何时网络达到了一个合理的稳定状态，或者是否需要终止当前的训练/求解过程。通常，以下几个条件可以用来决定迭代的停止：

7.1.1 迭代次数与能量变化的临界值

• 迭代次数限制 ：通常会设定一个最大迭代次数作为停止条件之一。这个限制可以防止程序无限运行，尤其是当网络陷入局部最小值时。
• 能量变化阈值 ：另一个常用的停止条件是连续多次迭代后，网络能量的变化小于一个预设的阈值。这表明网络可能已经接近稳定状态，因为能量函数的下降速率随着接近稳定状态而减慢。

7.1.2 停止条件对求解精度的影响

停止条件的选择直接影响到求解的精度和效率。过于宽松的条件可能导致网络未能达到最佳稳定状态，而过于严格可能会导致计算时间的浪费。实际应用中，需要在效率和精度之间做出权衡。

7.2 TSP问题求解结果的分析和解读

经过一系列迭代，Hopfield网络将输出TSP问题的近似解。网络稳定时，每个神经元的状态代表着TSP路径中的城市访问顺序。

7.2.1 解的正确性验证和路径重建

在得到一组稳定状态后，我们需要验证其正确性，并尝试重建出TSP的路径。

• 解的正确性验证 ：首先，检查所有神经元状态是否形成一个闭合回路，即路径是循环的。然后，验证路径是否满足TSP问题中规定的约束，例如，每个城市只访问一次。
• 路径重建 ：根据神经元的状态，可以重建出TSP问题的解。具体来说，可以将神经元状态映射回城市序列，形成访问每个城市的顺序。

7.2.2 结果分析与算法性能评估

对最终解的质量进行评估，通常会涉及以下几个方面：

• 路径长度 ：计算路径的总长度并与已知的最优解进行比较。
• 计算时间 ：记录算法从初始化到输出解的总时间，以评估算法的效率。
• 算法稳定性 ：多次运行算法以验证结果的稳定性和可靠性。

通过对结果的分析，我们可以对算法的性能有一个全面的认识，从而指导我们对算法进一步的优化和调整。

请注意，为了确保内容的连贯性，本章内容的编写假设读者对Hopfield网络和TSP问题有一定的了解。接下来的章节将深入探讨如何通过编程实现和优化这一过程。

本文还有配套的精品资源，点击获取

简介：Hopfield网络是一种模拟神经元交互的人工神经网络模型，用于解决旅行商问题（TSP），这是一个NP完全问题。本文介绍如何通过VC++实现Hopfield网络算法，包括权重初始化、状态更新、能量计算等步骤，来寻找TSP的近似解。实现过程中可能会遇到局部最小值问题，因此需要采取策略来提高解的质量。通过本项目，读者可以加深对Hopfield网络和优化算法的理解，并学会如何将理论应用到实际代码中。

本文还有配套的精品资源，点击获取