POJ - 2965 The Pilots Brothers' refrigerator （三种方法）（状压BFS 状压DFS 思维）

题目链接：

http://poj.org/problem?id=2965

题目：

The game “The Pilots Brothers: following the stripy elephant” has a quest where a player needs to open a refrigerator.

There are 16 handles on the refrigerator door. Every handle can be in one of two states: open or closed. The refrigerator is open only when all handles are open. The handles are represented as a matrix 4х4. You can change the state of a handle in any location [i, j] (1 ≤ i, j ≤ 4). However, this also changes states of all handles in row i and all handles in column j.

The task is to determine the minimum number of handle switching necessary to open the refrigerator.

Input

The input contains four lines. Each of the four lines contains four characters describing the initial state of appropriate handles. A symbol “+” means that the handle is in closed state, whereas the symbol “−” means “open”. At least one of the handles is initially closed.

Output

The first line of the input contains N – the minimum number of switching. The rest N lines describe switching sequence. Each of the lines contains a row number and a column number of the matrix separated by one or more spaces. If there are several solutions, you may give any one of them.

Sample Input

-+--
----
----
-+--

Sample Output

6
1 1
1 3
1 4
4 1
4 3
4 4

题目大意：

一个冰箱上有4*4共16个开关，改变任意一个开关的状态（即开变成关，关变成开）时，此开关的同一行、同一列所有的开关都会自动改变状态。要想打开冰箱，要所有开关全部打开才行。 输入：一个4×4的矩阵，+表示关闭，-表示打开； 输出：使冰箱打开所需要执行的最少操作次数，以及所操作的开关坐标。

题目分析：

首先是最暴力的想法，用一个16位的二进制数表示这16个开关的状态（比如0代表第一行第一列的开关  0*x+y代表x行y列的开关），0代表开，1代表关，当这个16位二进制数为0，则代表冰箱可以打开。

状压BFS：

对于每一个状态，我们都可以分别对16个开关进行操作，然后产生16个新的状态。然后我们开个数组标记一下，使每个状态只能出现一次，然后BFS这一颗16叉搜索树即可得到答案。（在普通的BFS上加路径记录）最多只有2^16种状态，复杂度完全在我们的接受范围之内。（具体实现见代码）

---

状压DFS：

首先，我们要知道开关的操作次序是没有任何影响的，先操作第x个开关再操作第y个开关 和 先操作第y个开关再操作第x个开关 是完全没有区别的，然后，还要知道，一个开关操作偶数次就相当于没有操作，操作奇数次就相当于操作了1次。也就是说每个开关其实只有操作1次和不操作这两种可能。所以我们从第一个开关搜索到最后一个开关，每一个开关要不然操作，要不然不操作。这样就形成了一颗2叉搜索树。第一次搜索到冰箱打开的状态就是最优的方案。同样记录一下路径即可。（学到了一种简单的方法）（具体实现看代码）

---

思维：

我们思考一下，能不能找到一种方案，使得只有一个位置的开关发生变化，如果能够找到这样的方案，那么我们就可以逐步的进行操作，从而打开冰箱。

幸运的是，这种方案是存在的。方案就是对所希望修改状态的开关所在的行列的所有开关都进行一次操作。如下图（数字代表状态改变次数 褐色代表我们想要改变状态的开关，红色代表同行同列的开关，黄色代表其他开关）

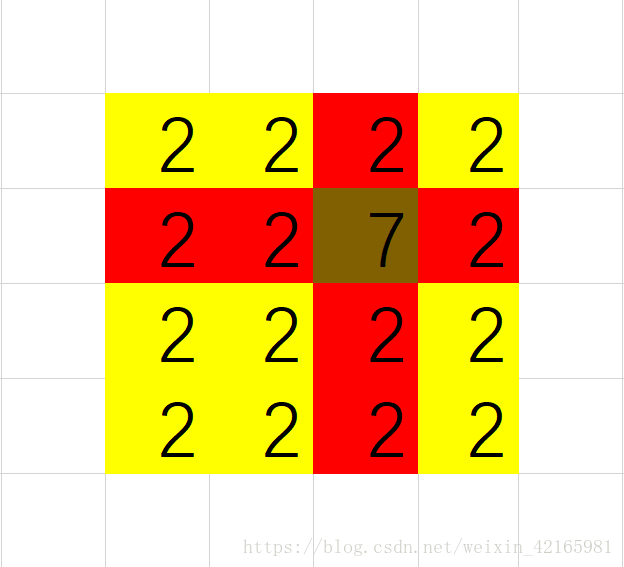
是不是很显然就得到了方案的证明。

这样我们的方案就确定了（依次对关闭的开关进行如上操作），那么，应该如何保证操作次数最小呢？因为刚刚说过，操作偶数次就相当于没有操作，奇数次就相当于操作1次，按照这个去除掉一些无用操作就可以得到正确答案了。（具体实现见代码）

代码：

1.状压BFS

#include<iostream>
#include<cstdio>
#include<algorithm>

using namespace std;
const int MAXN=1<<18;
struct node{
	int f,s,c;
}q[MAXN];
int head=0,tail=0;
bool vis[MAXN];

bool judge(int sta)
{
	return sta==0;
}

int change(int cur,int s)
{
	int t=cur/4;t*=4;
	for(int i=t;i<t+4;i++)
		s^=(1<<i);
	t=cur%4;
	for(int i=0;i<16;i+=4)
		s^=(1<<(i+t));
	s^=(1<<cur);
	return s;
}

void Print_ans(int s)
{
	if(q[s].f==-1)
		return;
	Print_ans(q[s].f);
	printf("%d %d\n",q[s].c/4+1,q[s].c%4+1);
}

int Get_ans(int s)
{
    if(q[s].f==-1)
        return 0;
    return Get_ans(q[s].f)+1;
}

int BFS()
{
	node now,temp;
	while(head<tail)
	{
		now=q[head];
		if(judge(now.s))
			return head;	
		for(int i=0;i<16;i++)
		{
			temp.s=change(i,now.s);
			temp.f=head;
			temp.c=i;
			if(vis[temp.s])
				continue;
			vis[temp.s]=true;
			q[tail++]=temp;
		}
		head++;
	}
	return -1;
}

int main()
{
	node temp;
	temp.f=-1;temp.s=0;temp.c=-1;
	char ch;
	for(int i=0;i<16;i++)
	{
		scanf(" %c",&ch);
		if(ch=='+')
			temp.s=temp.s|(1<<i);
	}
	q[tail++]=temp;
	vis[temp.s]=true;
	int ans=BFS();
	printf("%d\n",Get_ans(ans));
	Print_ans(ans);
	return 0;
}

2.状压DFS

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;
const int MAXN=1<<18;
bool vis[MAXN],path[20];

bool judge(int sta)
{
	return sta==0;
}

int change(int cur,int s)
{
	int t=cur/4;t*=4;
	for(int i=t;i<t+4;i++)
		s^=(1<<i);
	t=cur%4;
	for(int i=0;i<16;i+=4)
		s^=(1<<(i+t));
	s^=(1<<cur);
	return s;
}

void Print()
{
	int ans=0;
	for(int i=0;i<16;i++)
		if(path[i])
			ans++;
	printf("%d\n",ans);
	for(int i=0;i<16;i++)
		if(path[i])
			printf("%d %d\n",i/4+1,i%4+1);
}

void DFS(int sta,int step)
{
	if(judge(sta))
	{
		Print();
		exit(0);
	}
	if(step==16)
		return;
	DFS(sta,step+1);
	sta=change(step,sta);
	path[step]=true;
	DFS(sta,step+1);
	path[step]=false;
}

int main()
{
	int s=0;
	char ch;
	for(int i=0;i<16;i++)
	{
		scanf(" %c",&ch);
		if(ch=='+')
			s=s|(1<<i);
	}
	vis[s]=true;
	DFS(s,0);
	return 0;
}

3.思维

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;
char mp[10][10];
int num[10][10];

void add_vis(int x,int y)
{
	for(int i=1;i<=4;i++)
		num[x][i]++,num[i][y]++;
	num[x][y]--;
} 

int main()
{
	for(int i=1;i<=4;i++)
	{
		for(int j=1;j<=4;j++)
		{
			scanf(" %c",&mp[i][j]);
			if(mp[i][j]=='+')
				add_vis(i,j); 
		}
	}
	int ans=0;
	for(int i=1;i<=4;i++)
	{
		for(int j=1;j<=4;j++)
		{
			if(num[i][j]&1)
				ans++;
			else
				num[i][j]=0;	
		}
	}
	printf("%d\n",ans);
	for(int i=1;i<=4;i++)
		for(int j=1;j<=4;j++)
			if(num[i][j])
				printf("%d %d\n",i,j);
	return 0;
}