深入理解C语言中线性表的顺序与链式实现

本文还有配套的精品资源，点击获取

简介：本实验详细探讨了数据结构中线性表的两种实现方法：顺序表与链表。通过C语言的实践，学习顺序表的快速访问与线性存储，以及链表在插入删除操作中的灵活性。实验包含了线性表的基本概念，C语言指针与内存操作，链表和顺序表的具体操作实现，以及算法时间复杂度分析。此外，通过实验报告，学生可以记录并分析实验过程和结果，从而加深对数据结构概念和编程实践的理解。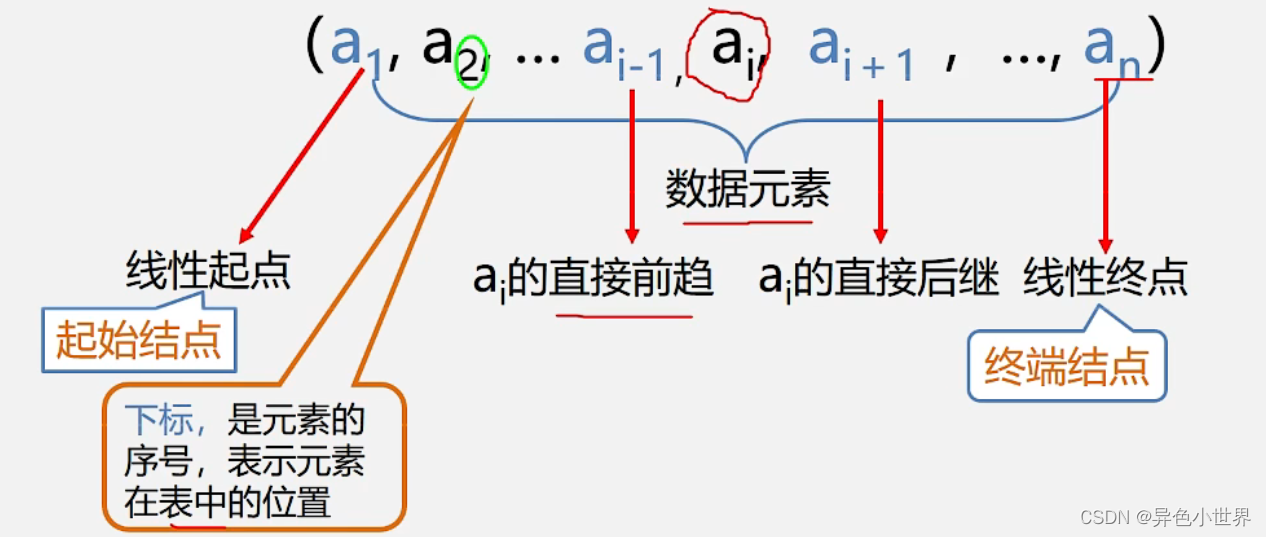

1. 线性表概念与重要性

在数据结构的世界里，线性表是一个基础且核心的概念。它代表了一个有序的元素集合，这些元素通过线性的方式进行排列，每个元素都与前一个和后一个元素有着直接的线性关系。线性表可以被看作是数据元素的一个简单集合，其中每个元素与前后元素仅有一个直接的前驱和后继关系。这一属性使得线性表的操作变得直观和简单，因此在算法设计和实际软件开发中，线性表被广泛应用。其重要性不仅在于能够高效地进行数据的存储与管理，还在于它作为其他复杂数据结构的基石，比如栈、队列、树和图等。理解线性表的基本概念及其重要性，对于深入学习和掌握高级数据结构是至关重要的。

2. 顺序表的特点与实现

2.1 顺序表的基本概念

2.1.1 顺序表的定义和特性

顺序表是一种线性表的顺序存储结构，它用一段连续的存储单元来存储线性表的数据元素。与链表相比，顺序表的最大特点在于能够利用元素的物理位置来反映其逻辑顺序，这使得顺序表在元素的随机访问方面具有天然的优势。

顺序表的特性包含以下几点： - 存储连续性 ：元素在内存中存储是连续的，每个元素都有一个确定的物理位置。 - 随机访问性 ：可以根据元素的索引直接访问该位置的元素，时间复杂度为O(1)。 - 固定大小 ：在未扩容的情况下，顺序表的容量是固定的，若超出容量需进行扩容操作。

2.1.2 顺序表的存储方式

顺序表的存储方式有两种基本类型：静态分配和动态分配。 - 静态分配 ：预先定义一个固定大小的数组空间，顺序表的大小在创建时就确定，无法改变。 - 动态分配 ：使用动态数组结构，如C++中的 vector ，可以根据需要动态地调整顺序表的大小。

例如，在C++中，静态分配的顺序表可以这样定义：

#define MAXSIZE 100 // 定义顺序表最大容量
typedef struct {
    ElemType data[MAXSIZE]; // 存储空间基址
    int length; // 当前长度
} SeqList;

动态分配的顺序表则会使用指针和动态内存分配函数：

#include <vector>
typedef std::vector<ElemType> SeqList;

2.2 顺序表的操作细节

2.2.1 元素的插入和删除

顺序表的插入操作需要移动插入位置后的所有元素，因此时间复杂度为O(n)。以下是使用C++进行元素插入的代码示例：

void insert(SeqList &L, int i, ElemType e) {
    if (L.length == MAXSIZE) { // 检查顺序表是否已满
        throw std::length_error("List is full");
    }
    if (i < 1 || i > L.length + 1) { // 检查插入位置的有效性
        throw std::out_of_range("Invalid position");
    }
    for (int k = L.length; k >= i; k--) { // 将第i个位置及之后的元素后移
        L.data[k] = L.data[k - 1];
    }
    L.data[i - 1] = e; // 在位置i处放入新元素
    L.length++; // 顺序表长度增1
}

删除操作同样涉及元素的移动，其代码逻辑与插入类似，但方向相反。删除第i个元素，将后面的元素向前移动一位，并更新顺序表长度。

2.2.2 元素的查找与访问

元素的查找和访问是顺序表的一大优势，由于顺序表元素的存储是连续的，访问任何元素的时间复杂度为O(1)。以下是查找元素的代码示例：

int search(SeqList &L, ElemType e) {
    for (int i = 0; i < L.length; i++) {
        if (L.data[i] == e) {
            return i + 1; // 返回元素的位置索引
        }
    }
    return 0; // 若未找到，返回0
}

在上述代码中，我们遍历顺序表，当找到匹配的元素时，返回该元素的位置索引。如果顺序表中不存在该元素，则返回0。

3. 链表的结构与类型

链表是一种在计算机科学中广泛使用的数据结构，它由一系列节点组成，每个节点包含数据部分和指向下一个节点的引用。与顺序表相比，链表具有动态的数据大小和灵活的内存管理特点，使得它在很多情况下成为更有效的选择。在深入链表操作之前，我们首先要了解链表的结构与类型。

3.1 链表的基本理论

3.1.1 链表的定义和分类

链表是一种物理上非连续、非顺序的数据结构，它通过指针将一系列零散的内存块连接起来。在链表中，每个节点包含两个部分：存储数据的区域和指向下一个节点的指针（称为链）。最后一个节点的指针通常指向一个空值，表示链表的结束。

链表根据节点间指针的不同，可以分为单向链表、双向链表和循环链表等类型。

• 单向链表 ：每个节点仅包含一个指针，只指向下一个个节点。
• 双向链表 ：每个节点包含两个指针，一个指向前一个节点，一个指向后一个节点。
• 循环链表 ：最后一个节点的指针指向链表的头部，形成一个环。

3.1.2 链表节点的设计与实现

链表的节点设计是实现链表的基础。每个节点通常包含数据字段和一个或多个指针字段。在编程实现时，我们可以定义一个链表节点的类或结构体。

以下是一个简单的单向链表节点的实现：

// C语言实现单向链表节点
typedef struct Node {
    int data;           // 数据字段
    struct Node* next;  // 指针字段，指向下一个节点
} Node;

// 初始化一个节点
Node* createNode(int value) {
    Node* newNode = (Node*)malloc(sizeof(Node)); // 动态分配内存
    if (newNode) { // 检查是否成功分配
        newNode->data = value; // 设置数据字段
        newNode->next = NULL;  // 初始化指针字段为NULL
    }
    return newNode;
}

在上述代码中，我们定义了一个名为 Node 的结构体，它包含一个整型数据 data 和一个指向下一个节点的指针 next 。 createNode 函数用于创建并初始化一个新的链表节点。

3.2 链表的详细操作

3.2.1 链表的创建和初始化

创建一个链表首先需要定义链表的头节点。头节点可以用来表示链表的开始，也可以用来保存链表的状态信息，如链表长度等。初始化一个空的链表，其头节点的指针通常指向NULL。

// C语言初始化链表头节点
Node* initLinkedList() {
    Node* head = createNode(0); // 创建头节点，数据部分设置为0或其他标识符
    if (head != NULL) {
        head->next = NULL; // 确保链表为空
    }
    return head;
}

3.2.2 链表节点的插入和删除

链表的操作主要包括插入和删除节点。插入节点时，需要先找到插入位置的前一个节点，然后创建新节点，并调整前一个节点的指针以及新节点的指针。删除节点时，需要将被删除节点前一个节点的指针指向被删除节点的下一个节点，然后释放被删除节点的内存。

以下是一个简单的插入操作示例：

// C语言实现链表节点的插入
void insertNode(Node** head, int value, int position) {
    Node* newNode = createNode(value);
    if (newNode == NULL) {
        return; // 插入失败
    }
    if (position == 0) {
        newNode->next = *head; // 插入到头节点
        *head = newNode;
    } else {
        Node* current = *head;
        for (int i = 0; current != NULL && i < position - 1; i++) {
            current = current->next; // 找到插入位置的前一个节点
        }
        if (current != NULL) {
            newNode->next = current->next; // 调整新节点的指针
            current->next = newNode;
        } else {
            free(newNode); // 插入失败，释放内存
        }
    }
}

在此代码中， insertNode 函数接受头节点的指针、要插入的值以及插入的位置。函数首先创建一个新的节点，然后根据位置将其插入到链表中。

请注意，由于篇幅限制，此部分只包含了插入节点的具体实现逻辑，而删除节点的实现逻辑和对应的代码将不再一一展示。但删除节点的过程与插入类似，也需调整节点的指针，并在操作完成后释放相应的内存。

通过本章节的介绍，我们了解了链表的基本理论和详细操作。下章节我们将深入探讨顺序表的动态操作以及线性表操作的实践应用。

4. 线性表操作实践

在前三章中，我们已经详细地探讨了线性表的相关理论，包括顺序表和链表的概念、特点、存储方式以及操作细节。现在，我们将通过实践案例来进一步理解这些理论知识，并实际操作如何使用顺序表和链表来解决具体问题。这将有助于加深我们对线性表操作的掌握，以及在实际开发中如何选择和使用线性表。

4.1 链表操作实战

链表作为一种基础且灵活的数据结构，在很多场景下都有广泛的应用。在这一部分，我们将通过实现链表的查找和遍历来深入理解链表的操作过程。

4.1.1 实现链表的查找和遍历

链表的查找通常指的是在链表中根据给定的键值查找相应的节点，而遍历则是访问链表中所有节点的过程。下面的代码展示了如何实现这些操作：

#include <stdio.h>
#include <stdlib.h>

// 定义链表节点
typedef struct Node {
    int data;
    struct Node *next;
} Node;

// 创建新节点
Node* createNode(int data) {
    Node *newNode = (Node*)malloc(sizeof(Node));
    if (!newNode) {
        return NULL;
    }
    newNode->data = data;
    newNode->next = NULL;
    return newNode;
}

// 插入节点到链表末尾
void insertNode(Node **head, int data) {
    Node *newNode = createNode(data);
    if (!newNode) {
        return;
    }
    if (*head == NULL) {
        *head = newNode;
    } else {
        Node *current = *head;
        while (current->next != NULL) {
            current = current->next;
        }
        current->next = newNode;
    }
}

// 链表查找
Node* findNode(Node *head, int key) {
    Node *current = head;
    while (current != NULL) {
        if (current->data == key) {
            return current;
        }
        current = current->next;
    }
    return NULL;
}

// 链表遍历
void traverseList(Node *head) {
    Node *current = head;
    while (current != NULL) {
        printf("%d ", current->data);
        current = current->next;
    }
    printf("\n");
}

int main() {
    Node *head = NULL;
    insertNode(&head, 1);
    insertNode(&head, 2);
    insertNode(&head, 3);
    printf("链表内容: ");
    traverseList(head);

    Node *found = findNode(head, 2);
    if (found) {
        printf("找到元素: %d\n", found->data);
    } else {
        printf("未找到元素\n");
    }
    // 释放链表内存
    Node *current = head;
    while (current != NULL) {
        Node *next = current->next;
        free(current);
        current = next;
    }
    return 0;
}

代码逻辑分析： - createNode 函数用于创建新的链表节点。 - insertNode 函数将新节点插入到链表的末尾。 - findNode 函数遍历链表，根据给定的键值查找节点。 - traverseList 函数遍历链表，打印出所有节点的数据。 - main 函数中创建了一个链表，并演示了如何插入节点、查找节点和遍历链表。 - 最后，代码遍历整个链表并释放了所有节点的内存，以避免内存泄漏。

4.1.2 链表操作的综合应用

接下来，我们将通过一个综合性的实例来演示链表操作的实际应用。设想我们需要一个有序链表，并且要实现它的增删查改操作。我们将创建一个简单的有序链表，并实现向链表中插入元素，保持链表有序，同时演示如何删除元素和查找元素。

// ... (前文定义的结构和函数代码)

// 在有序链表中插入节点
void sortedInsert(Node **head, int data) {
    Node *newNode = createNode(data);
    if (!newNode) {
        return;
    }
    if (*head == NULL || (*head)->data >= newNode->data) {
        newNode->next = *head;
        *head = newNode;
    } else {
        Node *current = *head;
        while (current->next != NULL && current->next->data < newNode->data) {
            current = current->next;
        }
        newNode->next = current->next;
        current->next = newNode;
    }
}

// 删除链表中的节点
void deleteNode(Node **head, int key) {
    Node *temp = *head, *prev = NULL;
    if (temp != NULL && temp->data == key) {
        *head = temp->next;
        free(temp);
        return;
    }
    while (temp != NULL && temp->data != key) {
        prev = temp;
        temp = temp->next;
    }
    if (temp == NULL) return;
    prev->next = temp->next;
    free(temp);
}

// 使用示例
int main() {
    Node *head = NULL;
    sortedInsert(&head, 10);
    sortedInsert(&head, 18);
    sortedInsert(&head, 4);
    sortedInsert(&head, 7);
    printf("插入后的有序链表: ");
    traverseList(head);
    deleteNode(&head, 7);
    printf("删除元素7后的链表: ");
    traverseList(head);
    Node *found = findNode(head, 18);
    if (found) {
        printf("找到元素: %d\n", found->data);
    } else {
        printf("未找到元素\n");
    }
    // ... (释放内存代码)
    return 0;
}

代码逻辑分析： - sortedInsert 函数在有序链表中插入新节点，保持链表的有序性。 - deleteNode 函数根据给定的键值从链表中删除节点。 - 在 main 函数的使用示例中，我们创建了一个有序链表，并演示了如何插入新节点，删除节点，以及查找节点。

通过以上实践案例，我们已经能够清楚地了解如何操作链表以及链表在实际开发中的应用场景。接下来，我们将进一步探讨顺序表的操作实践。

4.2 顺序表操作实战

顺序表作为一种连续存储的数据结构，相比链表有着更快的随机访问速度。在这一部分，我们将通过顺序表的初始化和扩容操作以及增删查改操作来深入理解顺序表的使用。

4.2.1 顺序表的初始化和扩容操作

顺序表的初始化通常是指创建一个指定大小的数组，用于存储顺序表中的元素。在某些情况下，为了提高空间利用率，顺序表可能需要动态地进行扩容操作。

#include <stdio.h>
#include <stdlib.h>

// 顺序表的最大容量
#define MAX_SIZE 100

// 顺序表的定义
typedef struct {
    int data[MAX_SIZE];
    int size;
} SeqList;

// 初始化顺序表
void initList(SeqList *list) {
    list->size = 0;
}

// 扩容顺序表
void expandList(SeqList *list, int capacity) {
    if (list->size + capacity > MAX_SIZE) {
        printf("超出顺序表的最大容量\n");
        return;
    }
    for (int i = 0; i < capacity; ++i) {
        list->data[list->size + i] = 0; // 假设用0初始化新元素
    }
    list->size += capacity;
}

// 向顺序表中插入元素
void insertElement(SeqList *list, int index, int value) {
    if (index < 0 || index > list->size) {
        printf("插入位置无效\n");
        return;
    }
    if (list->size >= MAX_SIZE) {
        printf("顺序表已满，无法插入\n");
        return;
    }
    expandList(list, 1);
    for (int i = list->size - 1; i >= index; --i) {
        list->data[i + 1] = list->data[i];
    }
    list->data[index] = value;
    list->size++;
}

int main() {
    SeqList myList;
    initList(&myList);
    printf("顺序表初始化后的大小: %d\n", myList.size);
    insertElement(&myList, 0, 10);
    printf("插入元素后的顺序表: ");
    for (int i = 0; i < myList.size; ++i) {
        printf("%d ", myList.data[i]);
    }
    printf("\n");
    // ... (其他顺序表操作)
    return 0;
}

代码逻辑分析： - initList 函数用于初始化顺序表。 - expandList 函数扩展顺序表的容量。 - insertElement 函数向顺序表中插入元素，并且在必要时进行扩容。 - 在 main 函数的使用示例中，我们创建了一个顺序表，并演示了如何初始化顺序表和向顺序表中插入元素。

4.2.2 顺序表的增删查改操作

现在，我们将详细地探讨如何进行顺序表的增、删、查、改操作。

// ... (前文定义的结构和函数代码)

// 删除顺序表中的元素
void deleteElement(SeqList *list, int index) {
    if (index < 0 || index >= list->size) {
        printf("删除位置无效\n");
        return;
    }
    for (int i = index; i < list->size - 1; ++i) {
        list->data[i] = list->data[i + 1];
    }
    list->size--;
}

// 查找顺序表中的元素
int findElement(SeqList *list, int key) {
    for (int i = 0; i < list->size; ++i) {
        if (list->data[i] == key) {
            return i;
        }
    }
    return -1; // 未找到返回-1
}

// 修改顺序表中的元素
void updateElement(SeqList *list, int index, int newValue) {
    if (index < 0 || index >= list->size) {
        printf("更新位置无效\n");
        return;
    }
    list->data[index] = newValue;
}

// 使用示例
int main() {
    SeqList myList;
    initList(&myList);
    insertElement(&myList, 0, 10);
    insertElement(&myList, 1, 20);
    insertElement(&myList, 2, 30);
    printf("顺序表中的元素: ");
    for (int i = 0; i < myList.size; ++i) {
        printf("%d ", myList.data[i]);
    }
    printf("\n");
    deleteElement(&myList, 1);
    printf("删除元素后的顺序表: ");
    for (int i = 0; i < myList.size; ++i) {
        printf("%d ", myList.data[i]);
    }
    printf("\n");
    int index = findElement(&myList, 10);
    if (index != -1) {
        printf("找到元素: %d 在索引位置 %d\n", myList.data[index], index);
    } else {
        printf("未找到元素\n");
    }
    updateElement(&myList, 0, 100);
    printf("修改后的顺序表: ");
    for (int i = 0; i < myList.size; ++i) {
        printf("%d ", myList.data[i]);
    }
    printf("\n");
    // ... (其他顺序表操作)
    return 0;
}

代码逻辑分析： - deleteElement 函数用于删除顺序表中的元素。 - findElement 函数用于查找顺序表中的元素。 - updateElement 函数用于修改顺序表中的元素。 - 在 main 函数的使用示例中，我们演示了顺序表的增加、删除、查找和修改操作，并打印了结果。

通过顺序表操作的实践，我们已经能够掌握如何高效地使用顺序表来存储和管理数据。接下来，我们将转向更加复杂的数据结构优化和算法实践。

5. 数据结构算法优化与实验报告撰写

5.1 算法时间复杂度分析

5.1.1 时间复杂度和空间复杂度基础

在软件开发中，理解算法的时间复杂度和空间复杂度对于优化程序性能至关重要。时间复杂度衡量的是算法执行时间随输入数据大小增加的变化趋势，而空间复杂度衡量的是算法运行所需存储空间随输入数据大小增加的变化趋势。

时间复杂度通常用大O符号表示，它表示的是上界。例如，一个时间复杂度为O(n)的算法，意味着算法的执行时间最多与输入数据的大小成线性关系。常见的复杂度级别从低到高排序如下：O(1) < O(log n) < O(n) < O(n log n) < O(n^2) < O(2^n) < O(n!)。

空间复杂度的计算方法与时间复杂度类似，它关注算法执行过程中所需的最大额外空间。同样地，空间复杂度也用大O符号表示，例如O(1)表示空间复杂度为常数级别，与输入数据的大小无关。

5.1.2 各类操作的时间复杂度分析

对基本的数据结构操作进行时间复杂度分析可以帮助我们识别性能瓶颈。以下是线性表中一些常见操作的时间复杂度分析：

• 顺序表查找 ：
• 顺序查找：O(n)。

• 二分查找（前提是顺序表已排序）：O(log n)。

• 顺序表插入/删除 ：

• 在表尾插入/删除：O(1)。

• 在表头或中间位置插入/删除：O(n)，需要移动后续所有元素。

• 链表查找 ：

• 查找：O(n)，必须从头节点开始遍历链表。

• 链表插入/删除 ：

• 在表尾插入/删除：O(1)，前提是有尾指针。
• 在链表中间位置插入/删除：O(1)，如果已知具体位置。

理解了各种操作的时间复杂度，我们可以根据应用场景选择合适的数据结构和算法。

5.2 实验报告的编写与分析

5.2.1 实验报告的结构与内容

实验报告是记录和传递实验结果的文档。一份结构良好的实验报告应该包括以下几个部分：

• 标题 ：清晰地描述实验的性质和主题。
• 摘要 ：简要总结实验的目的、方法、结果和结论。
• 引言 ：介绍实验的背景、理论基础和相关工作。
• 实验方法 ：详细说明实验的设计、使用的数据结构、测试用例和算法。
• 实验结果 ：展示实验数据，通常包括运行时间和内存消耗等。
• 分析与讨论 ：分析实验结果，讨论算法性能，提出可能的优化方向。
• 结论 ：总结实验的发现和结论。
• 参考文献 ：列出实验中引用的所有文献资料。

5.2.2 实验结果的分析方法

分析实验结果时，可以采用以下方法：

• 图表展示 ：使用表格和图形（如折线图、柱状图）直观地展示数据，帮助读者理解实验结果。

• 对比分析 ：将不同算法在同一条件下的结果进行对比，分析各自的优势和劣势。

• 极限情况分析 ：分析算法在极端情况下的表现，比如数据量极小或极大的情况。

• 性能指标分析 ：针对时间复杂度和空间复杂度的预测，分析算法的运行时间和空间占用是否符合预期。

实验报告撰写时要保持客观和准确，避免夸大或缩小实验结果，确保报告的真实性和可信度。

通过这样的分析与报告撰写，可以系统地掌握实验的全过程，为后续的研究或开发工作提供可靠依据。

本文还有配套的精品资源，点击获取

简介：本实验详细探讨了数据结构中线性表的两种实现方法：顺序表与链表。通过C语言的实践，学习顺序表的快速访问与线性存储，以及链表在插入删除操作中的灵活性。实验包含了线性表的基本概念，C语言指针与内存操作，链表和顺序表的具体操作实现，以及算法时间复杂度分析。此外，通过实验报告，学生可以记录并分析实验过程和结果，从而加深对数据结构概念和编程实践的理解。

本文还有配套的精品资源，点击获取